哈特倒置器

哈特反平行四邊形倒置器（哈特第一倒置器）的動畫
連桿長度：
  曲柄和固定桿: $a$

  曲柄： $b$ （中點固定）

  結合桿： $c$ （中點和其他桿件連結）
${\begin{aligned}b&<c\\[4pt]2a&<{\tfrac {1}{2}}b+{\tfrac {1}{2}}c\\[2pt]{\tfrac {1}{2}}c&<{\tfrac {1}{2}}b+2a\end{aligned}}$

哈特倒置器（Hart's inversor）屬於直線運動機構，是二種在無滑動件的條件下可以進行直線運動的機構^[1]。哈特倒置器是由数学家哈利·哈特（英语：Harry Hart）在1874至1875年發明，也在同一年發表^[1]^[2]。

哈特第一倒置器

哈特第一倒置器，也稱為哈特 W-frame，是以反平行四邊形為基礎。加上了固定點以及驅動臂後成為六桿連桿。可以用來將轉動運動轉換為完美的直線運動，其中固定點在短桿上，讓另一桿在圓弧上運動^[1]^[3]。

哈特第二倒置器

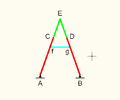
哈特 A-frame（哈特第二倒置器）的動畫
Link dimensions:^{[Note 1]}
  雙搖桿： $3 a + a$ （固定點之間距離： $2 b$ )

  結合桿： $b$

  A架的頂點： $2 a$

哈特第二倒置器，也稱為哈特 A-frame，在尺寸上的限制比較多^{[Note 1]}，不過其運動會沿著過二個固定點之間連線的中垂線。其外部類似大寫的A，是用梯形以及亖角形疊合而成。哈特第二倒置器也是六桿連桿。

尺寸舉例

以下是動畫中連桿的各桿尺寸。

- Hart's first inversor:
- AB = Bg = 2
- CE = FD = 6
- CA = AE = 3
- CD = EF = 12
- Cp = pD = Eg = gF = 6
- Hart's second inversor:
- AB = AC = BD = 4
- CE = ED = 2
- Af = Bg = 3
- fC = gD = 1
- fg = 2

相關條目

註

^ ^1.0 ^1.1 The current documented relationship between the links' dimensions is still heavily incomplete. For a generalization, refer to the following GeoGebra Applet: [Open Applet]

參考資料

^ ^1.0 ^1.1 ^1.2 True straight-line linkages having a rectlinear translating bar (PDF). [2016-04-13]. （原始内容存档 (PDF)于2016-01-24）.
^ International Symposium on History of Machines and Mechanisms.
^ Harts inversor (Has draggable animation). [2016-04-13]. （原始内容存档于2016-04-12）.

外部連結

维基共享资源上的相关多媒体资源：哈特倒置器

bham.ac.uk – Hart's A-frame (draggable animation) 6-bar linkage