反距离加权 (英語:inverse distance weighting ,IDW )是一种在有已知的离散数据点的情形下进行多元插值 确定性算法 。赋给未知点的值是用已知点的值的加權平均數 计算得出的。该算法也可在空间自相关分析(例如莫兰指数 )中用于构建空间权重矩阵。[ 1]
该方法的名称来自其加权的方式:未知点到每个已知点的距离的倒数。
对于给定的离散数据点,我们希望以一个函数
u
{\displaystyle u}
u
(
x
)
:
x
→
R
,
x
∈
D
⊂
R
n
,
{\displaystyle u(x):x\to \mathbb {R} ,\quad x\in \mathbf {D} \subset \mathbb {R} ^{n},}
其中
D
{\displaystyle \mathbf {D} }
N
{\displaystyle N}
元组 列表:
[
(
x
1
,
u
1
)
,
(
x
2
,
u
2
)
,
.
.
.
,
(
x
N
,
u
N
)
]
.
{\displaystyle [(x_{1},u_{1}),(x_{2},u_{2}),...,(x_{N},u_{N})].}
该函数应当是“平滑的”(连续且一次可微),确定的(
u
(
x
i
)
=
u
i
{\displaystyle u(x_{i})=u_{i}}
并行计算 )。
自1965年起,在哈佛计算机图形和空间分析实验室,各专业的科学家汇聚一堂,重新思考现在称作“地理信息系统 ”的各种问题。[ 2]
实验室工作的推动者霍华德·费舍尔(Howard Fisher)构思了一种改良的计算机绘图程序:SYMAP,其设计伊始,费舍尔就希望对插值进行改进。他向哈佛大学新生展示了SYMAP的进展,而后许多新生参与了实验室活动。一位大一新生唐纳德·谢泼德(Donald Shepard)决定对SYMAP中的插值法进行大改,随后发表了他1968年的著名论文。[ 3]
谢泼德的算法也受到William Warntz和实验室其他从事空间分析工作的人的理论方法的影响。他用距离的指数进行了许多实验,决定更接近重力模型(-2的指数)。谢泼德不仅实现了基本的反距离加权,还允许障碍(包括可渗透的和绝对的)插值。
其他研究机构此时也在研究插值,特别是堪萨斯大学 及其SURFACE II计划。但SYMAP的功能仍是最先进的,尽管是由本科生 编写的。
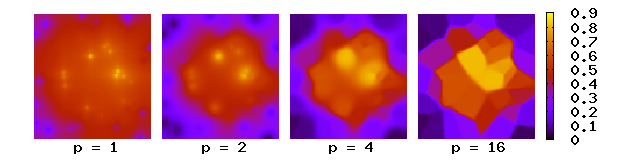
来自表面上的散点在不同幂参数p 下的谢泼德插值
z
=
exp
(
−
x
2
−
y
2
)
{\displaystyle z=\exp(-x^{2}-y^{2})}
给定一组样本点
{
x
i
,
u
i
|
for
x
i
∈
R
n
,
u
i
∈
R
}
i
=
1
N
{\displaystyle \{\mathbf {x} _{i},u_{i}|{\text{for }}\mathbf {x} _{i}\in \mathbb {R} ^{n},u_{i}\in \mathbb {R} \}_{i=1}^{N}}
u
(
x
)
:
R
n
→
R
{\displaystyle u(\mathbf {x} ):\mathbb {R} ^{n}\to \mathbb {R} }
u
(
x
)
=
{
∑
i
=
1
N
w
i
(
x
)
u
i
∑
i
=
1
N
w
i
(
x
)
,
if
d
(
x
,
x
i
)
≠
0
for all
i
,
u
i
,
if
d
(
x
,
x
i
)
=
0
for some
i
,
{\displaystyle u(\mathbf {x} )={\begin{cases}{\dfrac {\sum _{i=1}^{N}{w_{i}(\mathbf {x} )u_{i}}}{\sum _{i=1}^{N}{w_{i}(\mathbf {x} )}}},&{\text{if }}d(\mathbf {x} ,\mathbf {x} _{i})\neq 0{\text{ for all }}i,\\u_{i},&{\text{if }}d(\mathbf {x} ,\mathbf {x} _{i})=0{\text{ for some }}i,\end{cases}}}
其中
w
i
(
x
)
=
1
d
(
x
,
x
i
)
p
{\displaystyle w_{i}(\mathbf {x} )={\frac {1}{d(\mathbf {x} ,\mathbf {x} _{i})^{p}}}}
这是一个简单的反距离加权函数,其定义由谢泼德提出,[ 3] x 表示一个被插值点(未知点),x i
d
{\displaystyle d}
x i x 的给定距离(度规 算符),N 是插值中使用的已知点的总数,并且
p
{\displaystyle p}
其中,权重随着与已知点的距离的增加而减小。
p
{\displaystyle p}
p
{\displaystyle p}
沃罗诺伊图 ),每一个多边形内的数值几乎为恒定值。对于二维面,幂参数
p
≤
2
{\displaystyle p\leq 2}
ρ
{\displaystyle \rho }
r
0
{\displaystyle r_{0}}
R
{\displaystyle R}
∑
j
w
j
≈
∫
r
0
R
2
π
r
ρ
d
r
r
p
=
2
π
ρ
∫
r
0
R
r
1
−
p
d
r
,
{\displaystyle \sum _{j}w_{j}\approx \int _{r_{0}}^{R}{\frac {2\pi r\rho \,dr}{r^{p}}}=2\pi \rho \int _{r_{0}}^{R}r^{1-p}\,dr,}
其在
R
→
∞
{\displaystyle R\rightarrow \infty }
p
≤
2
{\displaystyle p\leq 2}
M 维,同样的结论适用于
p
≤
M
{\displaystyle p\leq M}
p
{\displaystyle p}
谢泼德法是最小化与插值点{x , u }的元组和插值点{x i ui }的i 元组 之间的偏差度量相关的函数的结果,定义为:
ϕ
(
x
,
u
)
=
(
∑
i
=
0
N
(
u
−
u
i
)
2
d
(
x
,
x
i
)
p
)
1
p
,
{\displaystyle \phi (\mathbf {x} ,u)=\left(\sum _{i=0}^{N}{\frac {(u-u_{i})^{2}}{d(\mathbf {x} ,\mathbf {x} _{i})^{p}}}\right)^{\frac {1}{p}},}
从最小化条件导出:
∂
ϕ
(
x
,
u
)
∂
u
=
0.
{\displaystyle {\frac {\partial \phi (\mathbf {x} ,u)}{\partial u}}=0.}
该方法容易扩展到其他维 数的空间,它实际上是将拉格朗日插值法 推广到多维空间。为三元插值设计的修改版算法由Robert J. Renka提出,Netlib的toms库中的算法661提供该算法。
Shepard法在一个维度下的插值,基于4个样本数据点,p = 2
谢泼德法的另一个修改版是仅使用半径R 范围内的最近邻(而不是完整样本)来计算插值。在这种情况下,权重略有修改:
w
k
(
x
)
=
(
max
(
0
,
R
−
d
(
x
,
x
k
)
)
R
d
(
x
,
x
k
)
)
2
.
{\displaystyle w_{k}(\mathbf {x} )=\left({\frac {\max(0,R-d(\mathbf {x} ,\mathbf {x} _{k}))}{Rd(\mathbf {x} ,\mathbf {x} _{k})}}\right)^{2}.}
当与快速空间搜索结构(如k-d树 )结合使用时,它即为适用于大尺度问题的高效N log N 插值方法。





![{\displaystyle [(x_{1},u_{1}),(x_{2},u_{2}),...,(x_{N},u_{N})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/639e496b90fb413c342ed159aad1f76d41278333)

















