卡諾熱機

卡諾熱機的軸向橫截面。在此圖中，abcd 是一個圓柱形容器，cd是一個可移動活塞，且A和B是定溫物體。容器可以與其中一個物體接觸或從兩者上移除。[1]

卡諾熱機[2]是卡諾循環的理論機器。這台機器的基本模型是由尼古拉·卡諾在1824年所提出的。卡諾熱機模型由埃米爾·克拉佩龍在1834年進行了擴展，並由魯道夫·克勞修斯在1857年進行了數學探索，產生了熵的基本熱力學概念。

每個熱力學系統都存在於特定的狀態。當一個系統經過一系列不同的狀態，最終回到它的初始狀態時，完成一個熱循環。熱機系統在經歷這個循環的過程中，可以對其周圍環境做功。

熱機的作用是將能量從高溫的區域轉移到低溫區域，並在此過程中將部分能量轉換為機械功。循環也可以逆向進行。該系統可能會受到外力的作用，且在此過程中，它可以將熱能從較冷的系統傳遞到較熱的系統，進而作為冷機或熱泵而非熱機。

卡諾循環圖

右圖源自卡諾1824年的著作《論火的動力（英语：Reflections on the Motive Power of Fire）》[3]，其中描述了“兩個物體A和B，每個都保持恆溫，且A溫度高於B。我們可以在不改變這兩個物體的溫度下給予或去除熱量，作為兩個無限熱量庫。我們將第一個稱為熱庫，第二個稱為冷庫。”[4]卡諾接著解釋了我們如何透過將一定量的熱量從“A”物體傳送到“B”物體來獲得動力，即“功”。此外，它還可以作為冷卻器，亦即冷機。

近代卡諾循環圖

卡諾循環圖 (近代) - 熱量 Q_H 從溫度T_H 的高溫熱庫，經過液態的「工作物質」和剩餘熱 Q_C 流入溫度 T_C的冷槽，藉由壓縮和膨脹的循環，使工作物質對環境作機械功 W 。

右圖為卡諾在討論理想熱機時使用的原始活塞和氣缸圖。右圖顯示了通用熱機的簡圖，例如卡諾熱機。在圖中，克勞修斯在1850年引入的術語“working body”（系統）可以是任何流體或蒸汽體，通過它時可以引入或流出熱量 Q 以產生功。卡諾假設流體可以是任何能夠膨脹的物質，例如水蒸氣、酒精蒸氣、汞蒸氣、永久性氣體、空氣等。儘管在早期，熱機有多種配置，通常 Q_H 由鍋爐供應，Q_C 通常由位於發動機單獨部件上的冷凝器以冷水形式去除。輸出功“W”通過活塞的運動傳遞，因為它用於轉動曲柄臂，而曲柄臂通常用於為滑輪提供動力，以便將水從鹽礦場中提出。卡諾將作功定義為“將物體提升某高度所需的能量”。

卡諾循環

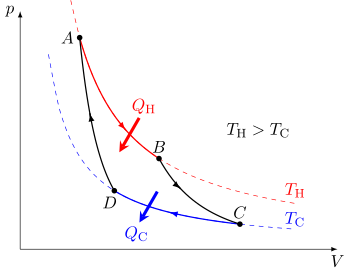
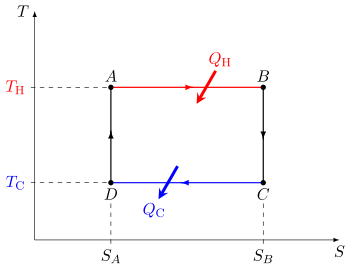
圖1：以P-V 圖解釋卡諾循環，以及所作的功

圖2：以溫度-熵圖解釋卡諾循環。循環在溫度 T_H 的熱庫和溫度 T_C 的冷庫間進行。 縱軸是溫度，橫軸是熵。

主条目：卡諾循環

熱機的卡諾循環包含以下步驟：

1. 氣體在溫度T_H 下的可逆等溫膨脹（等溫加熱）。

   在此步驟中（A 到 B）氣體膨脹並且它對周圍環境作功。溫度不會發生變化，因此膨脹是等溫的。氣體膨脹是通過吸收熱能 Q_H ，氣體熵 ${\displaystyle \Delta S_{\text{H}}=Q_{\text{H}}/T_{\text{H}}}$ 變大。

2. 等熵過程（可逆絕熱）氣體膨脹（等熵功輸出）。

   在此步驟中（B 到 C）假設活塞和氣缸是絕熱的，因此它們既不會獲得熱量，也不會失去熱量，氣體繼續膨脹，對周圍環境做功，並失去等量的內能。氣體膨脹使其冷卻到「冷」溫度，T_C。熵保持不變。

3. 氣體在溫度 T_C下的可逆等溫壓縮（等溫散熱）。

   在此步驟中（C 到 D）氣體暴露在低溫冷庫中，而周圍環境通過壓縮氣體對氣體做功（壓縮活塞），同時產生一定量的廢熱 Q_C < 0 ，流入冷庫，氣體熵 ${\displaystyle \Delta S_{\text{C}}=Q_{\text{C}}/T_{\text{C}}<0}$ 減少。（就數值而言，這與在步驟1中吸收的熵量相同。由於系統的多重性隨著體積的增加而減少，熵在等溫壓縮中減少。在此步驟中由周圍環境進行再壓縮所作的功小於步驟1中對周圍環境所做的功，因為它在溫度較低且低壓力下發生（即步驟3下的抗壓縮性低於步驟1下的膨脹力）。

4. 等熵過程（可逆絕熱）氣體壓縮（等熵功輸入）。

   在此步驟中（D 到 A）再次假設活塞和氣缸是絕熱的，並且移除了冷庫。在此步驟中，周圍環境繼續做功以進一步壓縮氣體。由於冷庫已被移除，溫度和壓力都會升高，這種額外的作功增加了氣體的內能，氣體被壓縮並導致溫度升高到 T_H。熵保持不變。此時氣體處於與步驟1開始時相同的狀態。

卡諾定理

主条目：卡諾定理 (熱力學)

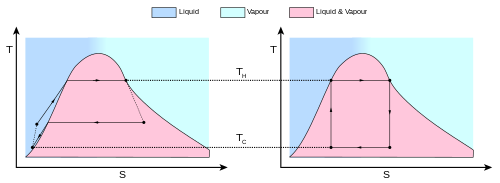
左圖為真實世界的熱機循環，右圖為理想熱機的卡諾循環。現實物質的熵隨溫度變化。這種變化由T-S圖上的曲線表示。對於該圖，曲線表示氣液平衡（見 朗肯循環）。不可逆的系統和熱量損失（例如摩擦力造成的熱量損失）使每一個步驟都無法成為理想狀態

卡諾定理是對這一事實的正式陳述：「在兩個儲熱器之間運行的發動機不會比在相同儲熱器之間運行的卡諾發動機更有效率。」

${\displaystyle \eta _{I}={\frac {W}{Q_{\mathrm {H} }}}=1-{\frac {T_{\mathrm {C} }}{T_{\mathrm {H} }}}}$

解釋

最大效率 ${\displaystyle \eta _{\text{I}}}$ 的定義如上：

W 系統所作的功，

${\displaystyle Q_{\text{H}}}$ 為進入系統的熱能，

${\displaystyle T_{\text{C}}}$ 為冷庫的絕對溫度，

${\displaystyle T_{\text{H}}}$ 為熱庫的絕對溫度。

卡諾定理的一個推論是：在相同溫度的熱庫和冷庫之間運行的可逆熱機效率相同。

當整個循環過程為可逆過程時，效率 η 為最大值。這意味著當“工作流體”完成一個循環並返回其原始狀態時，系統和環境的總熵（熱庫的熵、熱機的“工作流體”和冷庫的熵）保持不變（在不可逆過程和更現實的情況下，整個系統和周圍環境的總熵會增加）

由於“工作流體”經過一個循環後又回到原來的狀態，系統的熵是一個狀態函數，所以“工作流體”系統的熵變化為 0。因此熱庫和冷庫的總熵變化為零，過程可逆，發動機效率最大化。此推導將在下一節中進行。

熱機的性能係數（COP）是其效率的倒數。

真實熱機效率

對於真正的熱機，整個熱力學過程通常是不可逆的。工作流體經過一個循環後又回到初始狀態，因此流體系統的熵變為0，但在這一循環過程中冷熱庫的熵變化之和大於0。

流體的內能也是一個狀態變數，所以它在一個循環內的總變化量為0。 所以系統作的總功 W 等於進入系統的淨熱量, 吸收熱量 ${\displaystyle Q_{\text{H}}}$ > 0 ，且散出熱量 ${\displaystyle Q_{\text{C}}}$ < 0 的廢熱:[5]

${\displaystyle W=Q=Q_{\text{H}}+Q_{\text{C}}}$

2

對於真正的熱機，卡諾循環的第 1 階段和第 3 階段，熱量分別被來自熱儲器的“工作流體”吸收並釋放到冷儲器，不再保持理想可逆，並且在進行熱交換時，冷熱庫溫度與流體溫度之間存在溫差。

在熱從溫度${\displaystyle T_{\text{H}}}$的熱庫流入液體期間，液體溫度略低於${\displaystyle T_{\text{H}}}$，且流體可能不保持等溫。 令${\displaystyle \Delta S_{\text{H}}}$ 為流體在吸熱過程中的總熵變化。

${\displaystyle \Delta S_{\text{H}}=\int _{Q_{\text{in}}}{\frac {{\text{d}}Q_{\text{H}}}{T}}}$

3

其中流體的溫度T 總是略少於 ${\displaystyle T_{\text{H}}}$。

因此，我們得到：

${\displaystyle {\frac {Q_{\text{H}}}{T_{\text{H}}}}={\frac {\int {\text{d}}Q_{\text{H}}}{T_{\text{H}}}}\leq \Delta S_{\text{H}}}$

4

類似地，在從流體向冷庫注入熱量時，排熱過程中的流體總熵變化${\displaystyle \Delta S_{\text{C}}}$< 0 :

${\displaystyle \Delta S_{\text{C}}\geqslant {\frac {Q_{\text{C}}}{T_{\text{C}}}}<0}$

5

在熱量傳遞到冷庫的過程中，液體溫體T 總是略大於 ${\displaystyle T_{\text{C}}}$.

我們這裡只考慮了熵變化的數值。由於循環過程的流體系統的總熵變為 0，我們必須有

${\displaystyle \Delta S_{\text{H}}+\Delta S_{\text{C}}=\Delta S_{\text{cycle}}=0}$

6

將前面三個方程合併得到：[6]

${\displaystyle -{\frac {Q_{\text{C}}}{T_{\text{C}}}}\geqslant {\frac {Q_{\text{H}}}{T_{\text{H}}}}}$

7

合併方程 (2) 和 (7) 得到

${\displaystyle {\frac {W}{Q_{\text{H}}}}\leq 1-{\frac {T_{\text{C}}}{T_{\text{H}}}}}$

8

因此，

${\displaystyle \eta \leq \eta _{\text{I}}}$

9

其中 ${\displaystyle \eta ={\frac {W}{Q_{\text{H}}}}}$ 是真實熱機的效率，${\displaystyle \eta _{\text{I}}}$ 是卡諾熱機在溫度${\displaystyle T_{\text{H}}}$ 和 ${\displaystyle T_{\text{C}}}$的冷熱庫運轉的效率。對於卡諾熱機，整個過程為「可逆的」，方程(7) 等號成立。因此，真實引擎的效率總是低於理想的卡諾引擎。

公式 (7) 表示對於真實引擎系統和周圍環境（流體和冷熱庫）的總熵會增加，因為當 ${\displaystyle Q_{\text{C}}}$ 在固定溫度${\displaystyle T_{\text{C}}}$流入冷庫，其熵增加量為大於熱庫在固定溫度${\displaystyle T_{\text{H}}}$，流出熱量${\displaystyle Q_{\text{H}}}$ 所損失的熵。 不等式(7) 基本上就是 克勞修斯定理。

根據第二定理，“卡諾熱機的效率與工作物質的性質無關”。

註解

1. 圖 1 卡諾 (1824, p. 17) 和 卡諾 (1890, p. 63)。在圖中，容器的直徑大到足以連結A和B，但在模型中，容器不會同時與兩個物體接觸。此外，該圖包含了連接外部活塞的軸桿。
2. 卡諾以法文mechine à feu命名，瑟斯頓將其翻譯為「熱機」或「蒸汽機」。在腳註中，卡諾將熱機與一般的蒸汽機區分出來。（卡諾, 1824, p. 5 和 卡諾, 1890, p. 43）
3. Reflections on the Motive Power of Fire. [2022-01-17]. （原始内容存档于2020-01-23）. 
4. 威廉·瑟斯頓所譯 (卡諾, 1890, p. 51-52)。
5. Planck, M. Treatise on Thermodynamics. Dover Publications. 1945: 90. §90, eqs.(39) & (40) 
6. Fermi, E. Thermodynamics. Dover Publications (仍在印刷). 1956: 47. below eq.(63) 

外部連結

• Episode 46. Engine of Nature: The Carnot engine, part one, beginning with simple steam engines. The Mechanical Universe. Caltech –通过YouTube. 

參考資料

• Carnot, Sadi. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. Paris: Bachelier. 1824 （法语）.  (First Edition 1824) and (Reissued Edition of 1878)
• Carnot, Sadi. Thurston, Robert Henry , 编. Reflections on the Motive Power of Heat and on Machines Fitted to Develop That Power. New York: J. Wiley & Sons. 1890.  (full text of 1897 ed.) (Archived HTML version)