|
Попередня Аналітика
  Попередня Аналітика (грецька: Ἀναλυτικὰ Πρότερα; лат. Analytica Priora) — робота Арістотеля про дедукційні методи (силогізми). Попередня аналітика одна з шести збережених праць Арістотеля, присвячена логіці та науковому методу, частина того, що перипатетики називають Органоном. Термін «аналітика» походить від грецьких слів ἀναλυτός (analutos, розв'язний) та ἀναλύω (analuo, «вирішити», дослівно — «втратити»). В роботі Арістотеля дуже помітні відмінності в значенні слова «ἀναλύω» і споріднених з ним слів. Можливо, Арістотель запозичив використання цього слова від слова «аналіз», яке використовував його вчитель Платон. З іншого боку, значення, яке найкраще відповідає терміну аналітика, походить з геометрії: те, що Арістотель називав έπιστήμη епістема. Таким чином, процес аналізу полягає у знаходженні аргументованих фактів. Попередня Аналітика Арістотеля це перша в історії спроба науково дослідити логіку. Саме тому Арістотель вважається батьком логіки, як він сам казав у Софістичних Спростуваннях: «…Коли справа доходить до цього питання, не може бути такого, щоб частина була створена заздалегідь, а частина пізніше. Замість цього, взагалі нічого не існувало б.»[1] У Попередній аналітиці, Арістотель визначає силогізм як "висловлювання, в якому при стверджуванні чого-небудь випливає дещо, відмінне від стверджуваного". У наш час це визначення призвело до дискусії про те, як слід тлумачити слово "силогізм"[2]. Арістотель використовував цей термін у широкому спектрі дійсних аргументів. Деякі вчені вважають, що краще використовувати слово «дедукція» замість значення, яке дав Арістотель грецькому слову συλλογισμός, силогізм. У наш час "силогізм" використовується як метод прийняття висновку. «Силогізм» складається з трьох простих атрибутивних висловлювань: двох засновків і одного висновку. Засновки силогізму поділяють на більший (містить предикат висновку) і менший (містить суб'єкт висновку). За положенням середнього терму силогізми поділяють на фігури. А фігури поділяються за логічною формою засновків і висновку — на модуси. Аналітика Арістотеля складається з теоретичної частини, Попередньої аналітики, в якій розповідається про дедуктивну науку та практичної частини, Постаналітика[en], де описуються доведення Арістотеля. Попередня аналітика показує, що дедукція складається з трьох основних силогізмів, а Постаналітика це демонструє.[3] У третьому столітті нашої ери, Олександр Афродісій прокоментував Попередню аналітику як найкращу і найстарішу збережену пам'ятку історії, яка доступна англійською мовою.[4] У шостому столітті Боецій написав перший відомий латинський переклад Попередньої аналітики. Арістотель відкрив нові правила силогізму, за якими комбінація двох категоричних суджень, які відповідають цим правилам, у сумі дає правильне твердження. У силогізмі обов'язково повинно бути три атрибутних висловлювань. Арістотель ввів визначення фігури, яка відповідає категоричному силогізму і встановив спеціальні правила для цих фігур. У центрі його уваги знаходились три фігури. Четверту фігуру він вважав менш досконалою, ніж перші три, тому спеціально не аналізував її. Вивченням четвертої (недосконалої) фігури та її модусів займався учень Аристотеля — Теофраст. Силогізм Вчення Арістотеля про силогізм — перша логічна теорія дедукції. Арістотель використовує поняття змінної, що дозволяє сприймати процедуру прийняття висновку як формальний процес. Силогізм Арістотеля складається з логічних змінних і постійних висловлювань. Змінними висловлюваннями є букви А, В, С, які позначають найбільше, середнє і найменше висловлювання силогізму. Постійні логічні висловлювання відповідають таким відношенням:
У теорії силогізму головна мета Арістотеля була дослідити, які відношення між висловлюваннями утворюють правильні висновки, а які — ні. Силогістика знайшла застосування у розділі сучасної формальної логіки — численні предикатів. Більш детальне дослідження силогістики доводить, що Стагіріт, будуючи теорію дедукції, використовував численні висловлювання. У своїй праці «Метафізика» Стагіріт зазначив: «Із істинних висловлювань не можна утворити хибний висновок, однак із хибних висловлювань можна отримати істинний висновок, однак побачити причину, через яку воно істинне — неможливо». За часів середньовіччя виник і активно використовувався метод символізації. Цей метод значно спрощує дослідження Попередньої Аналітики: а = належить кожному е = нічому не належить і = чомусь належить о = чомусь не належить. У методі символізації позначення можуть виглядати абревіатурами: АаВ = А належить кожному В (кожне В — це А) АеВ = А не належить нічому з В (нічого з В не є А) АіВ = А належить чомусь із В (щось із В належить А) АоВ = А не належить чомусь із В (щось із В не є А). Спираючись на сучасну логіку, таким чином можуть бути представлені тільки декілька видів пропозицій. Структура простого категоричного силогізмуУ силогізмі існує рівно три терми:
Підмет S (суб'єкт) — відносно чого ми висловлюємось (буває двох видів):
Присудок P (предикат) — наше висловлювання (існує два види суджень):
Відношення між підметом і присудком:
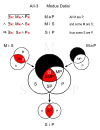
Під час визначення відношень між підметом і присудком дуже важлива чітка формалізація термів. Наприклад, безхатній пес, з точки зору проживання в будинку, не є домашньою твариною, однак, з точки зору приналежності за соціально-біологічною ознакою, пес належить до класу домашніх тварин. Слід розуміти, що «домашня тварина» зі соціально-біологічної класифікації в окремих випадках може бути «не домашньою твариною» з точки зору місця проживання, тобто зі соціально-побутового погляду. Три фігури (Темні зони — порожні, червоні — не порожні.) Відносно залежності положення середнього терму, Арістотель ділить силогізми на три види: силогізм в першій, другій та третій фігурі.
Три фігури можуть бути представлені таким чином:
Поняття про модуси силогізмуКожна фігура силогізму має певні модуси (від латинського modus, що означає «спосіб», «вид»). Модус силогізму — різновид фігур, які відрізняються одна від одної кількістю і якістю суджень, які складають засновки й висновок модуса. Модуси категоричного силогізму позначаються трьома великими літерами тих суджень, із яких побудовано силогізм. Якщо більший і менший засновки та висновок загальноствердні судження, то цей модус позначається AAA. Літери означають більший засновок, менший засновок і висновок, відповідно.
Теоретично кожен засновок може бути загальноствердним (А), загальнозаперечним (Е), частковоствердним (І) чи частковозаперечним (О), тоді можна припустити, що кожна фігура силогізму має по 16 модусів. Однак не всі сполучення засновків мають істинний висновок. Дійсних, правильних модусів силогізму значно менше. Для того щоб знайти, які модуси має кожна фігура, необхідно дотримуватись загальних правил категоричного силогізму та особливими правилами фігур. Силогізм у першій фігуріУ "Попередній Аналітиці", перекладеній А. Д. Дженкінсом, Арістотель казав про Першу фігуру: «… Якщо А — предикат всього В, а В — предикат всього С, А повинно бути предикатом всього С». В "Попередній Аналітиці", перекладеній Робіном Смітом, Арістотель казав про першу фігуру: «… Якщо А — предикат кожного з В, а В — предикат кожного з С, необхідно щоб А було предикатом кожного С.» Якщо взяти а = предикат всього = предикат кожного, і використати символічний метод середньовіччя, то перша фігура спрощується до: Якщо АаВ і ВаС, то АаС. Або так: АаВ, ВаС; тому АаС Коли чотири силогічні символи (а, у, і, о) знаходяться в першій фігурі, потрібно застосувати наступні діючі форми дедукції для першої фігури: AaB, BaC; тому AaC AeB, BaC; тому AeC AaB, BiC; тому AiC AeB, BiC; тому AoC У середньовіччі, через мнемонічні причини, вони були названі «Barbara», «Celarent», «Darii» та «Ferio», відповідно. Різниця між першою фігурою та іншими двома полягає в тому, що силогізм в першій фігурі існує доти, доки його немає в другій та третій фігурі. Це дуже важливо в теорії Арістотеля про силогізми: для першої фігури це — аксіома, а для другої і третьої фігури це потрібно доводити. Доведення другої та третьої фігури завжди посилається на першу фігуру. Силогізм у другій фігуріУ "Попередній Аналітиці" Арістотель казав: «…Якщо М належить кожному N, але не належить X, то Х також не належить М. Але М належить кожному N, тому Х не належить N». Цей вираз можна спростити за допомогою символів, що використовувалися у середньовіччі: Якщо MaN, але MeX, тому NeX. Якщо MeX, то XeM, але MaN, ось чому XeN. Коли чотири силогічні символи (а, у, і, о) знаходяться в другій фігурі, потрібно застосувати наступні діючі форми дедукції для першої фігури: MaN, MeX; тому NeX MeN, MaX; тому NeX MeN, MiX; тому NoX MaN, MoX; тому NoX У середньовіччі, через мнемонічні причини, вони були названі «Camestres», «Cesare», «Festino» та «Baroco», відповідно. Силогізм у третій фігуріУ "Попередній Аналітиці" Арістотель казав, «… Якщо щось належить всьому, а інше нічому, чи якщо вони обидва належать всьому, або нічому, я називаю таку фігуру третьою, посилаючись на універсальні терми. Тому якщо Р і R належать кожному S, то можливо що P буде належати чомусь із R». Спрощення: Якщо PaS і RaS, то PiR. Коли чотири силогічні символи (а, у, і, о) знаходяться в третій фігурі, потрібно застосувати наступні діючі форми дедукції для першої фігури: PaS, RaS; тому PiR PeS, RaS; тому PoR PiS, RaS; тому PiR PaS, RiS; тому PiR PoS, RaS; тому PoR PeS, RiS; тому PoR У середньовіччі, через мнемонічні причини, вони були названі «Darapti», «Felapton», «Disamis», «Datisi», «Bocardo» та «Ferison», відповідно. Таблиця силогізмівПереважна більшість із 256 можливих форм силогізмів — недійсні (їх висновок логічно не випливає з засновків). Наведена нижче таблиця показує можливі форми, деякі з цих форм іноді можуть призвести до екзистенційної помилки, тобто вони є недійсними, якщо вони згадують порожні категорії. Ці неоднозначні моделі позначено курсивом.
Користуючись правилами, форми можна перетворити на інші форми, всі форми можна перетворити на одну з форм першої фігури. Четверта фігураВ силогістиці Арістотеля, силогізми діляться на три фігури, враховуючи знаходження середнього терму в двох висловлюваннях. Четверта фігура, в якій середній терм — предикат у головному варіанті і об'єкт у другорядному, була додана учнем Арістотеля Теофрастом і не зустрічається в роботі Арістотеля, хоча є свідчення, що він знав про силогізм четвертої фігури. Ухвалення Арістотеля БулемУ вступі до «Законів логіки» Джон Коркоран[en] підкреслює, що Джордж Буль без заперечень прийняв «Логіку» Арістотеля. Коркоран написав послідовне порівняння Попередньої аналітики та Законів логіки. Наслідуючи Коркорана, Буль повністю прийняв і схвалив логіку Арістотеля. Створюючи своє логічне вчення, Арістотель спирався на відкриття Геракліта, Демокріта, Сократа, Платона та інших вчених античності. Проте саме він здійснив ряд геніальних відкриттів у галузі логіки та вперше систематично виклав науку логіки у вигляді самостійної дисципліни. Внутрішні посиланняПримітки
Посилання
|