Однозначно розфарбовуваний граф

Однозна́чно розфарбо́вуваний граф — це k-колірний граф, що допускає тільки одне (правильне) k-розфарбування (з точністю до перестановки кольорів).

Приклади

Повний граф є однозначно розфарбовуваним, оскільки існує лише одне допустиме розфарбування — кожній вершині призначається свій колір.

Будь-яке k-дерево однозначно розфарбовується в (k + 1) колір. Однозначно розфарбовуються в 4 кольори планарні графи — це точно графи Аполлонія, тобто планарні 3-дерева[1].

Властивості

Деякі властивості однозначно k-розфарбовуваного графа G з n вершинами і m ребрами:

  1. m ≥ (k — 1) n — k (k -1)/2 [2] [3]

Пов'язані концепції

Мінімальна недосконалість

Мінімально недосконалий граф — це граф, e якому будь-який підграф є досконалим. Видалення будь-якої вершини з мінімально недосконалого графа залишає однозначно розфарбовуваний підграф.

Однозначне розфарбування ребер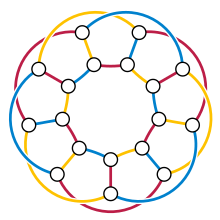

Однозначне 3-розфарбування ребер узагальненого графа Петерсена G(9,2)

Однозначно реберно-розфарбовуваний граф — це реберно k-колірний граф, що допускає тільки одне (правильне) реберне k-розфарбування з точністю до перестановки кольорів. Тільки шляхи та цикли допускають однозначне реберне 2-розфарбування. Для будь-якого значення k зірки K1,k є однозначно реберно k-розфарбовуваними графами. Проте Вільсон[4] висловив гіпотезу, а Томасон[5] довів, що за k ≥ 4 це єдині члени цього сімейства. Існують, однак, однозначно реберно 3-розфарбовувані графи, що не потрапляють до цієї класифікації, як, наприклад, граф трикутної піраміди.

Якщо кубічний граф однозначно реберно 3-розфарбовуваний, він повинен мати рівно три гамільтонових цикли, утворених ребрами двох (з трьох) кольорів, однак деякі кубічні графи тільки з трьома гамільтоновими циклами однозначного реберного 3-розфарбування не мають[6] . Будь-який простий планарний кубічний граф, що допускає єдине реберне 3-розфарбування, містить трикутник[1], але Тат[7] зауважив, що узагальнений граф Петерсена G(9,2) є непланарним графом без трикутників, однак він однозначно реберно 3-розфарбовуваний. Багато років цей граф був єдиним прикладом таких графів (див. статті Болобаша[8] і Швенка[9]), але тепер відомо нескінченно багато непланарних кубічних графів без трикутників, які мають однозначне реберне 3-розфарбування[6].

Однозначне тотальне розфарбування

Однозначно тотально розфарбовуваний граф — це тотально k-колірний граф, що допускає тільки одне (правильне) тотальне k-розфарбування (з точністю до перестановки кольорів).

Порожні графи[en], шляхи й цикли з довжиною, що ділиться на 3, є однозначно тотально розфарбовуваними графами. Махмудіан і Шокроллахі[10] висунули гіпотезу, что тільки ці графи й утворюють сімейство.

Деякі властивості однозначно тотально k-розфарбовуваного графа G з n вершинами:

  1. χ″(G) = Δ(G) + 1, крім випадку G = K2[11].
  2. Δ(G) ≤ 2 δ(G)[11].
  3. Δ(G) ≤ n/2 + 1[12].

Тут χ″(G) — тотальне хроматичне число; Δ(G) — найбільший степінь, а δ(G) — найменший степінь.

Примітки

  1. ↑ а б Fowler, 1998.
  2. ↑ Truszczyński, 1984.
  3. ↑ Xu, 1990.
  4. ↑ Wilson, 1976.
  5. ↑ Thomason, 1978.
  6. ↑ а б Belcastro, Haas, 2015.
  7. ↑ Tutte, 1976.
  8. ↑ Bollobás, 1978.
  9. ↑ Schwenk, 1989.
  10. ↑ Mahmoodian, Shokrollahi, 1995.
  11. ↑ а б Akbari, Behzad, Hajiabolhassan, Mahmoodian, 1997.
  12. ↑ Akbari, 2003.

Література

  • S. Akbari. Two conjectures on uniquely totally colorable graphs // Discrete Mathematics. — 2003. — Т. 266, вип. 1-3. — С. 41–45. — DOI:10.1016/S0012-365X(02)00797-5.
  • S. Akbari, M. Behzad, H. Hajiabolhassan, E. S. Mahmoodian. Uniquely total colorable graphs // Graphs and Combinatorics. — 1997. — Т. 13, вип. 4. — С. 305–314. — DOI:10.1016/S0012-365X(02)00797-5.
  • Sarah-Marie Belcastro, Ruth Haas. Triangle-free uniquely 3-edge colorable cubic graphs // Contributions to Discrete Mathematics. — 2015. — Т. 10, вип. 2. — С. 39–44. — arXiv:1508.06934.
  • Béla Bollobás. Extremal Graph Theory. — Academic Press, 1978. — Т. 11. — (LMS Monographs)
  • Thomas Fowler. Unique Coloring of Planar Graphs. — Georgia Institute of Technology Mathematics Department, 1998. — (Ph.D. thesis)
  • Christopher J. Hillar, Troels Windfeldt. Algebraic characterization of uniquely vertex colorable graphs // Journal of Combinatorial Theory. — 2008. — Т. 98, вип. 2. — С. 400–414. — (Series B). — DOI:10.1016/j.jctb.2007.08.004.
  • E. S. Mahmoodian, M. A. Shokrollahi. Combinatorics Advances. — Dordrecht; Boston; London : Kluwer Academic Publishers, 1995. — Т. 329. — С. 321–324. — (Mathematics and its applications)
  • Allen J. Schwenk. Enumeration of Hamiltonian cycles in certain generalized Petersen graphs // Journal of Combinatorial Theory. — 1989. — Т. 47, вип. 1. — С. 53–59. — DOI:10.1016/0095-8956(89)90064-6.
  • A. G. Thomason. Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977). — 1978. — Т. 3. — С. 259–268. — (Annals of Discrete Mathematics)
  • M. Truszczyński. Finite and Infinite Sets. Vol. I, II. Proceedings of the sixth Hungarian combinatorial colloquium held in Eger, July 6–11, 1981 / András Hajnal, László Lovász, Vera T. Sós. — North-Holland, Amsterdam, 1984. — Т. 37. — С. 733–748. — (Colloq. Math. Soc. János Bolyai)
  • William T. Tutte. Colloquio Internazionale sulle Teorie Combinatorie (Rome, 1973), Tomo I. — Accad. Naz. Lincei, Rome, 1976. — С. 193–199. Atti dei Convegni Lincei, No. 17.. Як процитовано в Белкастро й Гааса (Belcastro, Haas, 2015).
  • Shao Ji Xu. The size of uniquely colorable graphs // Journal of Combinatorial Theory. — 1990. — Т. 50, вип. 2. — С. 319–320. — (Series B). — DOI:10.1016/0095-8956(90)90086-F.
  • R. J. Wilson. Proc. British Comb. Conf. 1975. — Winnipeg : Utilitas Math, 1976. — С. 696.. Як процитовано в Томасона (Thomason, 1978).

Посилання