Непарний граф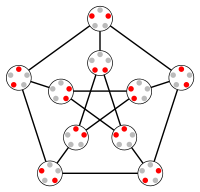

Граф Петерсена O₃ = KG_5,2
вершина = ${\displaystyle {\tbinom {2n-1}{n-1}}}$
ребер = ${\displaystyle n{\tbinom {2n-1}{n-1}}/2}$
діаметр = n − 1[1][2]
обхват=
  3 якщо n = 2,
  5 якщо n = 3,
  6 якщо n > 3[3]
властивість = дистанційно-транзитивний
позначення = O_n

Непарний граф O₄ = KG_7,3

В теорії графів непа́рні гра́фи O_n — це сімейство симетричних графів із високим непарним обхватом, визначених на деяких сімействах множин. Вони включають і узагальнюють графи Петерсена.

Визначення та приклади

Непарний граф O_n має одну вершину для кожної з (n − 1)-елементних підмножин множини з (2n — 1) елементів. Дві вершини пов'язані ребром тоді й лише тоді, якщо відповідні підмножини не перетинаються[4]. Так, O_n — це граф Кнезера KG(2n − 1,n − 1), O₂ — трикутник, а O₃ — знайомий граф Петерсена.

Узага́льнені непа́рні гра́фи включають непарні графи і складані кубічні графи^[en], і визначаються як дистанційно-регулярні графи з діаметром n − 1 і непарним обхватом 2n − 1 для деякого n[5].

Історія та застосування

Хоча графи Петерсена відомі від 1898 року, їх визначення як «непарних графів» датується роботою Ковальовскі[6], в якій він вивчає непарний граф O₄[2][6]. Непарні графи вивчають з огляду на їх використання в хімічній теорії графів під час моделювання зсуву йонів вуглецю^[en][7][8]. Їх також використовують як мережеву топологію при паралельних обчисленнях[9].

Позначення O_n для цих графів запропонував 1972 року[10] Норман Біггз^[en]. Біггз і Тоні Гардинер^[en] пояснюють назву непарних графів у неопублікованій монографії 1974 року — кожному ребру непарного графа можна зіставити єдиний елемент X, який є «odd man out» (що можна перекласти як «гравець без партнера виходить зі гри»), тобто елемент не належить жодній іншій підмножині, пов'язаній із вершинами, інцидентними даному ребру[11][12].

Властивості

Непарний граф O_n є регулярним графом степеня n. Він має ${\displaystyle {\tbinom {2n-1}{n-1}}}$ вершин і ${\displaystyle n{\tbinom {2n-1}{n-1}}/2}$ ребер. Таким чином, число вершин для n = 1, 2, … буде

1, 3, 10, 35, 126, 462, 1716, 6435 (послідовність A001700 з Онлайн енциклопедії послідовностей цілих чисел, OEIS).

Дистанція і симетрія

Якщо дві вершини в O_n відповідають множинам однакового розміру, що відрізняються k елементами, то можна отримати з першої другу за 2k кроків, на кожному кроці прибираючи або додаючи один елемент. Якщо 2k < n, то це найкоротший шлях. В іншому випадку можна знайти коротший шлях цього типу, якщо почати з доповняльної до другої множини, а потім отримати другу множину, зробивши ще один крок. Таким чином, діаметр графа O_n дорівнює n − 1[1][2].

Будь-який непарний граф 3-дуго-транзитивний — будь-який орієнтований триреберний шлях у непарному графі можна перевести в будь-який такий самий шлях за допомогою симетрії графа[13]. Непарні графи дистанційно-транзитивні, оскільки вони дистанційно-регулярні[2]. Як дистанційно-регулярні графи, вони однозначно визначаються своїм масивом перетинів — ніякий інший дистанційно-регулярний граф не може мати таких самих параметрів, що й непарний граф[14]. Однак всупереч високому ступеню симетрії, непарні графи O_n для n > 2 ніколи не є графами Келі[15].

Непарні графи з n ≥ 3 мають обхват шість. Однак, хоча вони і не є двочастковими графами, їхні непарні цикли набагато довші, а саме непарний граф O_n має непарний обхват 2n − 1. Якщо n-регулярний граф має діаметр n − 1, непарний обхват 2n − 1 і тільки n різних власних значень, він повинен бути дистанційно-регулярним. Дистанційно-регулярні графи діаметра n − 1 і непарного обхвату 2n − 1 відомі як узага́льнені непа́рні гра́фи і включають складані кубічні графи^[en] так само, як і самі непарні графи[5].

Незалежні множини і розмальовка вершин

Нехай O_n — непарний граф, визначений на (2n − 1)-елементних підмножинах множини X, і нехай x — елементи множини X. Тоді серед вершин O_n рівно ${\displaystyle {\tbinom {2n-2}{n-2}}}$ вершин відповідають множинам, які містять x. Оскільки всі ці множини містять x, вони не є неперетинними, і утворюють незалежну множину графа O_n. Таким чином, O_n має 2n − 1 різних незалежних множин розміру ${\displaystyle {\tbinom {2n-2}{n-2}}}$. Із теореми Ердеша — Ко — Радо^[en] випливає, що це максимальні незалежні множини графа O_n. Таким чином, число незалежності графа O_n дорівнює ${\displaystyle {\tbinom {2n-2}{n-2}}.}$ Більш того, будь-яка максимальна незалежна множина повинна мати такий вигляд, так що O_n має рівно 2n − 1 максимальних незалежних множин[2].

Якщо I — максимальна незалежна множина, утворена множиною, яка містить елемент x, то доповнення множини I — це множина вершин, що не містять x. Це доповнення породжує парування в G. Кожна вершина незалежної множини суміжна n вершинам парування, а кожна вершина парування суміжна n − 1 вершинам незалежної множини[2]. Зважаючи на цей розклад і з огляду на те, що непарні графи не є двочастковими, вони мають хроматичне число рівне трьом — вершинам максимальної незалежної множини можна призначити один колір, а два інших кольори отримаємо з парування, породженого доповненням.

Реберне розфарбування

За теоремою Візінга число кольорів, необхідних для розфарбування ребер непарного графа O_n, дорівнює або n, або n + 1, і у випадку графів Петерсена O₃ воно дорівнює n + 1. Якщо n — степінь двох, число вершин у графі непарне, звідки знову випливає, що число кольорів у реберному розфарбуванні дорівнює n + 1[16]. Однак O₅, O₆ і O₇ можна розфарбувати n кольорами[2][16].

Біггз[10] пояснює цю задачу такою історією: одинадцять футболістів у вигаданому місті Кроам хочуть утворити пари команд для міні-футболу (одна людина залишається судити зустріч) усіма 1386 різними способами і хочуть скласти розклад ігор між усіма парами, при цьому шість ігор кожної команди мають гратися в різні дні тижня, за відсутності ігор у неділю. Чи можливо це? У цій історії кожна гра представляє ребро O₆, всі дні представлені кольорами, а реберне розфарбування в 6 кольорів графа O₆ дає розклад.

Непарні графи і гамільтонові графи

Граф Петерсена O₃ — це добре відомий негамільтонів граф, але було показано, що графи від O₄ до O₁₄ містять гамільтонові цикли[8][17][18][19]. Строгіше, комбінуючи задачу пошуку гамільтонових циклів і реберного розфарбування, можна розбити ребра графа O_n (для n = 4, 5, 6, 7) на найближче знизу ціле від (n/2) гамільтонових циклів. Якщо n непарне, решта ребер утворюють досконале поєднання[2][16]. Для n = 8, непарне число вершин в O_n не дозволяє розфарбувати ребра у 8 кольорів, але не закриває можливості розкладання на чотири гамільтонових цикли.

Гіпотеза Ловаса про гамільтонів цикл припускає, що кожен непарний граф має гамільтонів шлях і що кожен непарний граф O_n з n ≥ 4 має гамільтонів цикл.

Примітки

1. Norman L. Biggs. Automorphic graphs and the Krein condition // Geometriae Dedicata. — 1976. — Вип. 5 (3 січня). — С. 117—127. — DOI:10.1007/BF00148146.
2. Biggs, 1979
3. Douglas B. West. Introduction to Graph Theory. — 2nd. — Englewood Cliffs, NJ : Prentice-Hall, 2000. — С. 17.
4. Weisstein, Eric W. Odd Graph(англ.) на сайті Wolfram MathWorld.
5. Edwin Van Dam, Willem H. Haemers. An Odd Characterization of the Generalized Odd Graphs. — 2010. — 3 січня.
6. A. Kowalewski. W. R. Hamilton's Dodekaederaufgabe als Buntordnungproblem // Sitzungsber. Akad. Wiss. Wien (Abt. IIa). — 1917. — Т. 126 (3 січня). — С. 67—90, 963—1007. Як процитовано в Біггза (Biggs, 1979).
7. Alexandru T. Balaban, D. Fǎrcaşiu, R. Bǎnicǎ. Graphs of multiple 1, 2-shifts in carbonium ions and related systems // Rev. Roum. Chim.. — 1966. — Т. 11 (3 січня). — С. 1205.
8. Alexandru T. Balaban. Chemical graphs, Part XIII: Combinatorial patterns // Rev. Roumaine Math. Pures Appl.. — 1972. — Т. 17 (3 січня). — С. 3—16.
9. Arif Ghafoor, Theodore R. Bashkow. A study of odd graphs as fault-tolerant interconnection networks // IEEE Transactions on Computing. — 1991. — Т. 40, вип. 2 (3 січня). — С. 225—232. — DOI:10.1109/12.73594.
10. Norman Biggs. Research Problems // American Mathematical Monthly. — 1972. — Т. 79, вип. 9 (3 січня). — С. 1018—1020.
11. Andries Brouwer, Arjeh M. Cohen, A. Neumaier. Distance-regular Graphs. — 1989. — 3 січня. — ISBN 0-387-50619-5.
12. Ed Pegg, Jr. Cubic Symmetric Graphs. — Mathematical Association of America, 2003. — 3 січня. Архівовано з джерела 21 серпня 2010.
13. László Babai. [1] / Ronald L. Graham, Martin Grötschel, László Lovász. — North-Holland, 1995. — Т. I. — С. 1447—1540. Архівовано з джерела 11 червня 2010
14. Aeryung Moon. Characterization of the odd graphs O_k by parameters // Discrete Mathematics. — 1982. — Т. 42, вип. 1 (3 січня). — С. 91—97. — DOI:10.1016/0012-365X(82)90057-7.
15. C. D. Godsil. More odd graph theory // Discrete Mathematics. — 1980. — Т. 32, вип. 2 (3 січня). — С. 205—207. — DOI:10.1016/0012-365X(80)90055-2.
16. Guy H. J. Meredith, E. Keith Lloyd. The footballers of Croam // Journal of Combinatorial Theory, Series B. — 1973. — Т. 15 (3 січня). — С. 161—166. — DOI:10.1016/0095-8956(73)90016-6.
17. Guy H. J. Meredith, E. Keith Lloyd. Combinatorics (Proc. Conf. Combinatorial Math., Math. Inst., Oxford, 1972). — Southend : Inst. Math. Appl, 1972. — 3 січня. — С. 229—236.
18. Michael Mather. The Rugby footballers of Croam // Journal of Combinatorial Theory, Series B. — 1976. — Т. 20 (3 січня). — С. 62—63. — DOI:10.1016/0095-8956(76)90066-6.
19. Ian Shields, Carla D. Savage. A note on Hamilton cycles in Kneser graphs // Bulletin of the Institute for Combinatorics and Its Applications. — 2004. — Т. 40 (3 січня). — С. 13—22. Архівовано з джерела 30 серпня 2017. Процитовано 2022-03-03.

Література

• Norman Biggs. Second International Conference on Combinatorial Mathematics. — 1979. — Т. 319 (3 січня). — С. 71—81. — DOI:10.1111/j.1749-6632.1979.tb32775.x.