Граф Татта — Коксетера

Граф Татта — Корсетера
Названо на честь	Вільям Татт Гарольд Коксетер
Вершин	30
Ребер	45
Радіус	4
Діаметр	4
Обхват	8
Автоморфізм	1440 (Aut(S6))
Хроматичне число	2
Хроматичний індекс	3
Число черг	2
Властивості	кубічний граф симетричний граф клітка граф Мура дистанційно-регулярний граф дистанційно-транзитивний граф двочастковий

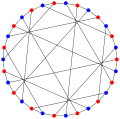
У математичній області теорії графів, граф Татта — Коксетера являє собою 3-регулярний граф з 30 вершинами і 45 ребрами. Як єдиний найменший кубічний граф обхвату 8, він є клітиною і графом Мура. Також це двочастковий граф і він може бути побудований як граф Леві узагальненого чотирикутника W₂ (відомий як конфігурація Кремони — Річмонда. Граф був названий на честь Вільяма Томаса Татта і Х. С. М. Коксетера; був відкритий Таттом (1947), але його зв'язок з геометричними конфігураціями був досліджений обома авторами спільно, результати викладені в опублікованих статтях (Татт 1958; Кокстер 1958).

Всі кубічні дистанційно-регулярні графи відомі.[1] Граф Татта — Кокстера є одним з 13 таких графів.

Конструкції і автоморфізм

Особливо проста комбінаторна побудова графа Татта — Коксетера можлива завдяки роботі Коксетера (1958b), яка заснована на роботі Сильвестра (1844). У сучасній термінології, візьмемо повний граф на 6 вершин K₆. Він має 15 ребер, а також 15 парувань. Кожна вершина графа Татта — Коксетера відповідає ребру або паруванню з K₆, і кожне ребро графа Татта — Коксетера пов'язує узгодження K₆ до кожного з трьох складових ребер.

На основі цієї конструкції, Коксетер показав, що граф Татта — Коксетера — симетричний граф; він має групу з 1440 автоморфізмів, які можуть бути ідентифіковані за допомогою автоморфізмів групи перестановок на шести елементах (Коксетер, 1958b). Внутрішні автоморфізми^[en] цієї групи відповідають перестановці шести вершин графа specification; ці перестановки діють на граф Татта — Коксетера перестановкою вершин на кожній стороні його поділу на дві частини, зберігаючи при цьому кожну з двох сторін фіксованою у вигляді набору. Крім того, зовнішні автоморфізми групи^[en] перестановок міняють одну сторону двочасткового графа на іншу. Як показав Коксетер, будь-який шлях до п'яти ребер в графі Татта — Коксетера еквівалентний будь-якому іншому такому шляху на один такий автоморфізм.

Галерея

• 
  Хроматичне число графа Татта - Корсетера дорівнює 2.
• 
  Хроматичний індекс графа Татта - Корсетера дорівнює 3.

Примітки

1. Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance-Regular Graphs. New York: Springer-Verlag, 1989.

• Coxeter, H. S. M. (1958a). The chords of the non-ruled quadric in PG(3,3). Canad. J. Math. 10: 484—488. doi:10.4153/CJM-1958-047-0.

• Coxeter, H. S. M. (1958b). Twelve points in PG(5,3) with 95040 self-transformations. Proceedings of the Royal Society A. 247 (1250): 279—293. doi:10.1098/rspa.1958.0184. JSTOR 100667.

• Sylvester, J. J. (1844). Elementary researches in the analysis of combinatorial aggregation. Phil. Mag. Series 3. 24: 285—295.

• Tutte, W. T. (1947). A family of cubical graphs. Proc. Cambridge Philos. Soc. 43 (4): 459—474. doi:10.1017/S0305004100023720.

• Tutte, W. T. (1958). The chords of the non-ruled quadric in PG(3,3). Canad. J. Math. 10: 481—483. doi:10.4153/CJM-1958-046-3.

Посилання

• François Labelle. 3D Model of Tutte's 8-cage. Архів оригіналу за 9 квітня 2009. Процитовано 27 березня 2016.
• Weisstein, Eric W. Levi Graph(англ.) на сайті Wolfram MathWorld.
• Exoo, G. «Rectilinear Drawings of Famous Graphs.» [1] [Архівовано 24 червня 2021 у Wayback Machine.]