Виявлення циклу

В інформатиці виявлення циклу — це алгоритмічна задача пошуку циклу в послідовності ітераційних значень функції.

Для будь-якої функції f, яка відображає скінченну множину S на саму себе, і будь-якого початкового значення x₀ з S, послідовність ітераційних значень функції

${\displaystyle x_{0},\ x_{1}=f(x_{0}),\ x_{2}=f(x_{1}),\ \dots ,\ x_{i}=f(x_{i-1}),\ \dots }$

зрештою буде двічі використовувати одне й те ж значення, тобто знайдеться пара різних індексів i та j таких, що x_i = x_j. Як тільки це трапиться, послідовність буде періодично продовжуватися, повторюючи ту саму послідовність значень від x_i до x_{j − 1}. Виявлення циклу — це задача пошуку i та j для заданих f та x₀.

Відомо кілька алгоритмів швидкого знаходження циклів з незначним використанням пам'яті. Алгоритм черепахи та зайця Роберта У. Флойда переміщує два вказівника з різною швидкістю по послідовності значень, поки обидва не вкажуть на рівні значення. Алгоритм Брента базується на ідеї експоненціального пошуку^[en]. Алгоритми Флойда і Брента використовують сталий об'єм пам'яті, а кількість разів обчислення значеннь функції пропорційна відстані від початку послідовності до першого повторення. Кілька інших алгоритмів використовують більший об'єм пам'яті для меншої кількості обчислень значень функції.

Серед застосунків виявлення циклів є перевірка якості генераторів псевдовипадкових чисел та криптографічних хеш-функцій, алгоритмів обчислювальної теорії чисел, виявлення нескінченних циклів у комп'ютерних програмах та періодичних конфігурацій у клітинних автоматах, автоматизований аналіз форми^[en] в таких структурах даних, як зв'язаний список, взаємне блокування при обробці транзакцій в СУБД.

Приклад

Функція, яка відображає множину {0,1,2,3,4,5,6,7,8} на саму себе, та її граф.

На малюнку показана функція f, яка відображає множину S={0,1,2,3,4,5,6,7,8} саму до себе. Якщо починати з x₀ = 2 і послідовно знаходити f, отримаємо послідовність значень функції: 2, 0, 6, 3, 1, 6, 3, 1, 6, 3, 1, ...

Циклом у цій послідовності буде підпослідовність 6, 3, 1.

Визначення

Нехай S — будь-яка скінченна множина, f — будь-яка функція, що відображає S на саму себе, ${\displaystyle x_{0}}$ — будь-який елемент з S. Для будь-якого ${\displaystyle i>0}$ нехай ${\displaystyle x_{i}=f(x_{i-1})}$. Нехай μ — найменший індекс, для якого значення x_μ знову з'являється нескінченно часто в межах послідовності значень x_i, а λ (довжина петлі) — це найменше натуральне число, що x_μ = x_{λ + μ}. Проблема виявлення циклу — це задача пошуку λ і μ.[1]

Цю ж задачу розглянемо с точки зору теорії графів: побудуємо орієнтований граф (у якому кожна вершина має єдине вихідне ребро), якому відповідає граф функції нашої задачі, та вершинами якого є елементи множини S, а ребра якого відображають елемент на відповідне значення функції, як показано на малюнку. Набір вершин доступних від початкової вершини x₀ утворюють підграф форми, що нагадує грецьку букву rho (ρ): шлях довжини μ від x₀ до цикла, який складається з λ вершин.[2]

Комп'ютерне представлення

Як правило, f не буде вказано таблицею значень, як це показано на малюнку вище. Швидше за все, алгоритму виявлення циклу може бути наданий доступ або до послідовності значень x_i, або до підпрограми для обчислення f. Завдання полягає в тому, щоб знайти λ і μ, перевіряючи якомога менше значень з послідовності або виконуючи якомога менше викликів підпрограм. Як правило, також важлива просторова складність алгоритму для проблеми виявлення циклу: бажано вирішити цю проблему, використовуючи обсяг пам'яті, значно менший, ніж потрібно для збереження всієї послідовності.

У деяких додатках, і зокрема в ρ-алгоритм Полларда для факторізації цілих чисел, алгоритм має набагато обмежений доступ до S та f. Наприклад, в ρ-алгоритмі Полларда S — це набір цілих чисел за модулем невідомого простого множника числа, що підлягає факторизації, тому навіть розмір S невідомий алгоритму. Щоб дозволити алгоритмам виявлення циклу використовувати такі обмежені знання, вони можуть бути розроблені на основі наступних можливостей. Спочатку передбачається, що алгоритм має у своїй пам'яті об'єкт, що представляє вказівник на початкове значення x₀. На будь-якому етапі він може виконати одну з трьох дій: він може скопіювати будь-який вказівник, який він має, на інший об'єкт у пам'яті, він може застосувати f і замінити будь-який з його покажчиків на вказівник на наступний об'єкт у послідовності, або він може застосувати підпрограма для визначення того, чи є два її покажчики рівними значеннями в послідовності. Дія тестування рівності може включати деякі нетривіальні обчислення: наприклад, в ρ-алгоритмі Полларда це реалізується шляхом перевірки того, чи має різниця між двома збереженими значеннями нетривіальний найбільший спільний дільник з числом, яке потрібно врахувати.[2] У цьому контексті, за аналогією до моделі обчислень покажчикової машини^[en], алгоритм, який використовує лише копіювання покажчика, просування в межах послідовності та тести рівності, можна назвати алгоритмом покажчика.

Алгоритми

Якщо вхід подається як підпрограма для обчислення f, задачу виявлення циклу можна тривіально вирішити, використовуючи лише λ + μ, просто обчисливши послідовність значень x_i та використовуючи структуру даних, таку як хеш-таблицю для їх зберігання значення та перевірити, чи кожне наступне значення вже збережено. Проте просторова складність цього алгоритму пропорційна λ + μ, надмірно велика. Крім того, для реалізації цього методу як алгоритму вказівників^[en] знадобиться застосувати тест рівності до кожної пари значень, що призведе до загального квадратичного часу. Таким чином, дослідження в цій галузі зосереджені на двох цілях: використати менше місця, ніж цей наївний алгоритм, і знайти алгоритми покажчиків, які використовують менше тестів рівності.

Черепаха і заєць Флойда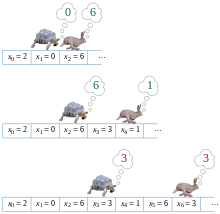

Алгоритм виявлення циклу «черепаха і заєць» Флойда, застосований до послідовності 2, 0, 6, 3, 1, 6, 3, 1, …

Алгоритм пошуку циклу Флойда — це алгоритм покажчиків, який використовує лише два покажчики, які рухаються по послідовності з різною швидкістю. Його також називають «алгоритмом черепахи та зайця», натякаючи на байку Езопа про «Черепаху та зайця».

Алгоритм названий на честь Роберта У. Флойда, якому його винахід приписував Дональд Кнут.[3][4] Однак алгоритм не з'являється у опублікованій роботі Флойда, і це може бути хибним віднесенням: Флойд описує алгоритми перерахування всіх простих циклів в орієнтованому графі у роботі 1967 року[5] але ця робота не описує проблему пошуку циклу у графах функцій, що є темою цієї статті. Насправді, твердження Кнута (1969 року), яке він приписує Флойду без цитування, є першим відомим згадуванням у друкованому вигляді, і, отже, він може належати до математичного фольклору^[en] і не належати окремій особі.[6]

Ключове розуміння алгоритму наступне. Якщо існує цикл, то для будь-яких цілих чисел i ≥ μ і k ≥ 0, x_i = x_{i + kλ}, де λ — довжина петлі, яку потрібно знайти, а μ — індекс першого елемента циклу. Виходячи з цього, тоді можна показати, що i = kλ ≥ μ для деякого k тоді і тільки тоді, коли x_i = x_2i.

Таким чином, алгоритму потрібно лише перевірити наявність повторюваних значень цієї спеціальної форми, одна вдвічі далі від початку послідовності, ніж інша, щоб знайти період ν повторення, кратний λ. Як тільки ν буде знайдено, алгоритм відновлює послідовність від її початку, щоб знайти перше повторене значення x_μ у послідовності, використовуючи той факт, що λ ділить ν і, отже, x_μ = x_{μ + v}. Нарешті, як тільки значення μ стало відомим, тривіально знайти довжину λ найкоротшого повторюваного циклу шляхом пошуку першого положення μ + λ для якого x_{μ + λ} = x_μ.

Таким чином, алгоритм утримує два вказівники у даній послідовності: один (черепаха) у точці x_i, а інший (заєць) у точці x_2i. На кожному кроці алгоритму він збільшується i на один, рухаючи черепаху на один крок вперед, а зайця на два кроки вперед у послідовності, а потім порівнює значення послідовності за цими двома вказівниками. Найменше значення i > 0 для якого черепаха та заєць вказують на рівні значення, є бажаним значенням ν.

Наступний код Python показує, як ця ідея може бути реалізована як алгоритм.

def floyd(f, x0):
# Основна фаза алгоритму: пошук повторень x_i = x_2i.
   # Заєць рухається вдвічі швидше черепахи та
   # відстань між ними збільшується на 1 на кожному кроці.
   # Врешті -решт вони обидва опиняться всередині циклу, а потім,
   # в певний момент відстань між ними буде
   # ділиться на крапку λ.
  tortoise = f(x0) # f (x0) - елемент/вузол поруч із x0.
   hare = f (f (x0))
  while tortoise != hare:
    tortoise = f(tortoise)
    hare = f(f(hare))
 
  # На цьому місці розташування черепахи ν, що також дорівнює
   # на відстань між зайцем і черепахою ділиться на
   # період λ. Тож зайці рухаються по колу крок за кроком,
   # і черепаха (скинути на x0) рухаються до кола, буде
   # перетинаються на початку кола. Тому що
   # відстань між ними є постійною на 2ν, кратною λ,
   # вони погодяться, як тільки черепаха досягне індексу μ.
   # Знайдіть позицію μ першого повторення.

  mu = 0
  tortoise = x0
  while tortoise != hare:
    tortoise = f(tortoise)
    hare = f(hare)  # Заєць і черепаха рухаються з однаковою швидкістюd
    mu += 1
 
# Знайдіть довжину найкоротшого циклу, починаючи з x_μ
     # Заєць рухається крок за кроком, поки черепаха нерухома.
     # lam збільшується, поки не знайдеться λ.
     
  lam = 1
  hare = f(tortoise)
  while tortoise != hare:
    hare = f(hare)
    lam += 1
 
  return lam, mu

Цей код звертається лише до послідовності шляхом зберігання та копіювання покажчиків, оцінок функцій та тестів рівності; тому він кваліфікується як алгоритм вказівників. Алгоритм використовує O(λ + μ) цих типів та O(1) простір для зберігання.[7]

Алгоритм Брента

Річард П. Брент^[en] описав альтернативний алгоритм виявлення циклу, який, як і алгоритм черепахи та зайця, вимагає лише двох вказівників у послідовності.[8] Однак він базується на іншому принципі: пошук найменшої потужності з двох 2^i, більшої як за λ і за μ.

Для i = 0, 1, 2, ..., алгоритм порівнює x_2^i−1 з кожним наступним значенням послідовності до наступного степеня двох, зупиняючись, коли знаходить відповідність. Він має дві переваги порівняно з алгоритмом черепахи та зайця: він безпосередньо знаходить правильну довжину λ циклу, замість того, щоб шукати його на наступному етапі, а його кроки передбачають лише одну оцінку f, а не три.[9]

Наступний код Python більш детально показує, як працює ця техніка.

def brent(f, x0):
 
  # основний етап: пошук степеня двійки
  power = lam = 1
  tortoise = x0
  hare = f(x0) # f (x0) - елемент/вузол поруч із x0.
  while tortoise != hare:
    if power == lam: # час почати нову степінь двійки?
      tortoise = hare
      power *= 2
      lam = 0
    hare = f(hare)
    lam += 1

 # Знайдіть позицію першого повторення довжини λ
  tortoise = hare = x0
  for i in range(lam):
# range(lam) створює список зі значеннями 0, 1, ..., lam-1
    hare = f(hare)
  # Відстань між зайцем і черепахою тепер λ.

  # Далі заєць і черепаха рухаються з однаковою швидкістю, поки вони не домовляться
  mu = 0
  while tortoise != hare:
    tortoise = f(tortoise)
    hare = f(hare)
    mu += 1
 
  return lam, mu

Як і алгоритм черепахи та зайця, це алгоритм вказівників, який використовує O(λ + μ) та оцінки функцій та O(1) простір для зберігання. Не важко показати, що кількість оцінок функцій ніколи не може бути вище, ніж для алгоритму Флойда. Брент стверджує, що в середньому його алгоритм пошуку циклу працює приблизно на 36 % швидше, ніж алгоритм Флойда, і що він швидше ρ-алгоритма Полларда приблизно на 24 %. Він також виконує аналіз середніх випадків^[en] для рандомізованої версії алгоритму, в якому послідовність індексів, відстежена повільнішим із двох покажчиків, — це не повноваження двох самих, а скоріше рандомізоване кратне ступеням двох. Хоча його основне призначення — алгоритми цілочисельної факторизації, Брент також обговорює застосування для тестування генераторів псевдовипадкових чисел.[8]

Алгоритм Госпера

Алгоритм Р.В. Госпера^[en][10][11] знаходить період ${\displaystyle \lambda }$ і нижню ${\displaystyle \mu _{l}}$ і верхню ${\displaystyle \mu _{u}}$ межу вихідної точки першого циклу. Різниця між нижньою та верхньою межею має той самий порядок, що й період, наприклад. ${\displaystyle \mu _{l}+\lambda \sim \mu _{h}}$.

Головною особливістю алгоритму Госпера є те, що він ніколи не створює резервних копій для переоцінки функції генератора, і є економічним як у просторі, так і в часі. Його можна приблизно охарактеризувати як паралельну версію алгоритму Брента. У той час як алгоритм Брента поступово збільшує розрив між черепахою та зайцем, алгоритм Госпера використовує кілька черепах (збережено кілька попередніх значень), які приблизно експоненціально рознесені. Відповідно до примітки в пункті 132 HAKMEM [Архівовано 15 вересня 2020 у Wayback Machine.], цей алгоритм буде виявляти повторення до третього входження будь-якого значення, наприклад. цикл повторюватиметься максимум двічі. У цій примітці також зазначено, що її достатньо для зберігання ${\displaystyle \Theta (\log \lambda )}$ попередні значення; однак, передбачена реалізація[10] зберігає ${\displaystyle \Theta (\log(\mu +\lambda ))}$ цінності. Наприклад: значення функції-це 32-розрядні цілі числа, і апріорі відомо, що друга ітерація циклу закінчується після щонайменше 2^32 оцінок функції з початку, тобто. ${\displaystyle \mu +2\lambda \leq 2^{32}}$. Тоді достатньо зберегти 33 32-розрядні цілі числа.

На ${\displaystyle i}$-го оцінювання функції генератора, алгоритм порівнює отримане значення з ${\displaystyle O(\log i)}$ попередні значення; зауважте це ${\displaystyle i}$ піднімається принаймні ${\displaystyle \mu +\lambda }$ і максимум ${\displaystyle \mu +2\lambda }$. Тому складність цього алгоритму у часі дорівнює ${\displaystyle O((\mu +\lambda )\cdot \log(\mu +\lambda ))}$. Так як він зберігається ${\displaystyle \Theta (\log(\mu +\lambda ))}$ цінностей, її просторова складність становить ${\displaystyle \Theta (\log(\mu +\lambda ))}$. Це за звичайного припущення, наявного у цій статті, що розмір значень функції постійний. Без цього припущення складність простору така ${\displaystyle \Omega (\log ^{2}(\mu +\lambda ))}$ оскільки нам принаймні потрібно ${\displaystyle \mu +\lambda }$ різні значення, а отже, розмір кожного значення ${\displaystyle \Omega (\log(\mu +\lambda ))}$.

Компроміси між часом і простором

Ряд авторів вивчали методи виявлення циклів, які використовують більше пам'яті, ніж методи Флойда та Брента, але виявляють цикли швидше. Загалом ці методи зберігають декілька попередньо обчислених значень послідовності та перевіряють, чи кожне нове значення дорівнює одному з попередньо обчислених значень. Для того, щоб зробити це швидко, вони зазвичай використовують хеш-таблицю або подібну структуру даних для зберігання попередньо обчислених значень, і тому не є алгоритмами покажчиків: зокрема, вони зазвичай не можуть бути застосовані до ρ-алгоритма Полларда. Ці методи відрізняються тим, як вони визначають, які значення зберігати. Слідом за Нівашем[12] ми коротко оглядаємо ці методи.

• Брент[8] вже описував варіанти його методу, в яких індекси збережених значень послідовностей є степенями числа R відмінними від двох. Вибираючи R як число, близьке до одиниці, і зберігаючи значення послідовностей в індексах, які знаходяться поблизу послідовності послідовних повноважень R, алгоритм виявлення циклу може використовувати ряд оцінок функцій, які знаходяться в межах довільно малого коефіцієнта оптимуму λ + μ.[13][14]
• Седжвик^[en], Шиманьский и Яо[15] надають метод, який використовує M комірок пам'яті і вимагає лише в найгіршому випадку ${\displaystyle (\lambda +\mu )(1+cM^{-1/2})}$ оцінки функцій для деякої сталої c, яку вони показують як оптимальну. Методика передбачає збереження числового параметра d, зберігання в таблиці лише тих позицій у послідовності, кратних d, а також очищення таблиці та подвоєння d коли зберігається занадто багато значень.
• Кілька авторів описали методи виділених точок, які зберігають значення функцій у таблиці на основі критерію, що включає значення, а не індекси (як у методі Седжвіка та ін.).[16][17] Простіше кажучи, Ніваш[12] приписує Д. П. Вудраффу пропозицію зберегти випадкову вибірку раніше побачених значень, зробивши відповідний випадковий вибір на кожному кроці, щоб вибірка залишалася випадковою.
• Ніваш[12] описує алгоритм, який не використовує фіксований обсяг пам'яті, але для якого очікуваний обсяг використовуваної пам'яті (за припущення, що функція введення є випадковою) є логарифмічним по довжині послідовності. Елемент зберігається в таблиці пам'яті за допомогою цієї техніки, коли попередній елемент не має меншого значення. Як показує Ніваш, елементи з цією технікою можна підтримувати за допомогою стека, і кожне наступне значення послідовності потрібно порівнювати лише з верхньою частиною стека. Алгоритм завершується, коли знайдено повторюваний елемент послідовності з найменшим значенням. Запуск одного і того ж алгоритму з кількома стеками, з використанням випадкових перестановок значень для впорядкування значень у кожному стеку, дозволяє знайти компроміс у просторі часу, подібний до попередніх алгоритмів. Однак навіть версія цього алгоритму з одним стеком не є вказівним алгоритмом через порівняння, необхідні для визначення того, яке з двох значень менше.

Будь-який алгоритм виявлення циклу, який зберігає не більше M значень із вхідної послідовності, повинен виконувати принаймні ${\displaystyle (\lambda +\mu )\left(1+{\frac {1}{M-1}}\right)}$ оцінки функцій.[18][19]

Застосування

Виявлення циклів має багато застосувань.

• Визначення довжини циклу генератора псевдовипадкових чисел є одним із показників його сили. Це додаток, наведене Кнутом при описі методу Флойда.[3] Брент[8] описує результати тестування лінійного конгруенціального генератора таким чином; його період виявився значно меншим за рекламований. Для більш складних генераторів послідовність значень, у яких слід знайти цикл, може відображати не вихід генератора, а його внутрішній стан.
• Кілька теоретично численних алгоритмів ґрунтуються на виявленні циклу, включаючи ρ-алгоритма Полларда для цілочисельної факторизації[20] та пов'язаний з ним алгоритм кенгуру для задачі дискретного логарифма.[21]
• У криптографії можливість знайти два різних значення x_μ−-1 і х _λ+μ−-1 відображається з допомогою деяких криптографічного функції ƒ до того ж значення х_μ може вказувати на слабкість в ƒ. Наприклад, Quisquater та Delescaille[17] застосовують алгоритми виявлення циклу у пошуку повідомлення та пару стандартних ключів шифрування даних, які відображають це повідомлення на одне й те саме зашифроване значення; Каліскі, Рівест та Шерман[22] також використовують алгоритми виявлення циклу для атаки на DES. Цей метод також може бути використаний для пошуку колізій у криптографічній хеш-функціях.[23]
• Виявлення циклу може бути корисним як спосіб виявлення нескінченних циклів у певних типах комп'ютерних програм.[24]
• Періодичні конфігурації в моделюванні клітинних автоматів можна знайти, застосувавши алгоритми виявлення циклу до послідовності станів автоматів.[12]
• Аналіз форми^[en] зв'язаних списків — це метод перевірки правильності алгоритму, що використовує ці структури. Якщо вузол у списку неправильно вказує на попередній вузол у цьому ж списку, структура сформує цикл, який може бути виявлений цими алгоритмами.[25] У мові Common Lisp принтер S-виразів при змінній *print-circle* виявляє зациклені спискові структури і друкує їх компактно.
• Теске[14] описує застосування в обчислювальній теорії груп: визначення структури абелевої групи з набору її твірних. Криптографічні алгоритми Каліського та ін.[22] також можна розглядати як спробу зробити висновок про структуру невідомої групи.
• Fich коротко згадує додаток для комп'ютерного моделювання небесної механіки, яке вона приписує Вільяму Кехену. У цьому додатку виявлення циклу у фазовому просторі орбітальної системи може бути використано для визначення того, чи є система періодичною з точністю до моделювання.[18]
• У фрактальній генерації множини Мандельброта використовуються деякі техніки виконання для прискорення генерації зображення. Одна з них називається «перевірка періоду», яка полягає у знаходженні циклів на точковій орбіті. У цій статті описано техніку «перевірки періоду». Ви можете знайти інше пояснення тут [Архівовано 27 квітня 2021 у Wayback Machine.]. Деякі алгоритми виявлення циклу повинні бути реалізовані для реалізації цієї техніки.

Примітки

1. Joux, Antoine (2009), Algorithmic Cryptanalysis, CRC Press, с. 223, ISBN 9781420070033, архів оригіналу за 2 серпня 2021, процитовано 16 серпня 2021.
2. Joux, (2009).
3. Дональд Кнут. Seminumerical Algorithms // The Art of Computer Programming. — 3rd. — Massachusetts : Addison–Wesley, 1997. — Т. 2. — 762 с. — ISBN 0-201-89684-2.(англ.)
4. Handbook of Applied Cryptography, by Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone, p. 125 [Архівовано 2 серпня 2021 у Wayback Machine.], describes this algorithm and others
5. Флойд, Роберт (1967), Nondeterministic Algorithms, J. ACM, 14 (4): 636—644, doi:10.1145/321420.321422
6. The Hash Function BLAKE, by Jean-Philippe Aumasson, Willi Meier, Raphael C.-W. Phan, Luca Henzen (2015), p. 21 [Архівовано 17 серпня 2021 у Wayback Machine.], footnote 8
7. Joux, (2009), Section 7.1.1, Floyd's cycle-finding algorithm, pp. 225—226.
8. Р. П. Брент^[en] (1980), An improved Monte Carlo factorization algorithm (PDF), BIT Numerical Mathematics, 20 (2): 176—184, doi:10.1007/BF01933190, архів оригіналу (PDF) за 24 вересня 2009, процитовано 16 серпня 2021 {{citation}}: Перевірте значення |last= (довідка).
9. Joux, (2009), Section 7.1.2, Brent's cycle-finding algorithm, pp. 226—227.
10. Archived copy. Архів оригіналу за 14 квітня 2016. Процитовано 8 лютого 2017.
11. Архівована копія. Архів оригіналу за 15 вересня 2020. Процитовано 16 серпня 2021.
12. Nivasch, Gabriel (2004), Cycle detection using a stack, Information Processing Letters, 90 (3): 135—140, doi:10.1016/j.ipl.2004.01.016.
13. Schnorr, Claus P.; Lenstra, Hendrik W. (1984), A Monte Carlo factoring algorithm with linear storage, Mathematics of Computation, 43 (167): 289—311, doi:10.2307/2007414, JSTOR 2007414.
14. Teske, Edlyn (1998), A space-efficient algorithm for group structure computation, Mathematics of Computation, 67 (224): 1637—1663, Bibcode:1998MaCom..67.1637T, doi:10.1090/S0025-5718-98-00968-5.
15. Robert Sedgewick; Szymanski, Thomas G.; Yao, Andrew C.-C. (1982), The complexity of finding cycles in periodic functions, SIAM Journal on Computing, 11 (2): 376—390, doi:10.1137/0211030.
16. van Oorschot, Paul C.; Wiener, Michael J. (1999), Parallel collision search with cryptanalytic applications, Journal of Cryptology, 12 (1): 1—28, doi:10.1007/PL00003816, архів оригіналу за 16 серпня 2021, процитовано 16 серпня 2021.
17. Quisquater, J.-J.; Delescaille, J.-P., How easy is collision search? Application to DES, Advances in Cryptology – EUROCRYPT '89, Workshop on the Theory and Application of Cryptographic Techniques, Lecture Notes in Computer Science, т. 434, Springer-Verlag, с. 429—434, doi:10.1007/3-540-46885-4_43.
18. Fich, Faith Ellen (1981), Lower bounds for the cycle detection problem, Proc. 13th ACM Symposium on Theory of Computing, с. 96—105, doi:10.1145/800076.802462.
19. Allender, Eric W.; Klawe, Maria M. (1985), Improved lower bounds for the cycle detection problem, Theoretical Computer Science (journal)|Theoretical Computer Science, 36 (2–3): 231—237, doi:10.1016/0304-3975(85)90044-1.
20. Pollard, J. M. (1975), A Monte Carlo method for factorization, BIT, 15 (3): 331—334, doi:10.1007/BF01933667.
21. Pollard, J. M. (1978), Monte Carlo methods for index computation (mod p), Mathematics of Computation, American Mathematical Society, 32 (143): 918—924, doi:10.2307/2006496, JSTOR 2006496.
22. Kaliski, Burton S., Jr.; Rivest, Ronald L.; Sherman, Alan T. (1988), Is the Data Encryption Standard a group? (Results of cycling experiments on DES), Journal of Cryptology, 1 (1): 3—36, doi:10.1007/BF00206323.
23. Joux, (2009), Section 7.5, Collisions in hash functions, pp. 242—245.
24. Van Gelder, Allen (1987), Efficient loop detection in Prolog using the tortoise-and-hare technique, Journal of Logic Programming, 4 (1): 23—31, doi:10.1016/0743-1066(87)90020-3.
25. Auguston, Mikhail; Hon, Miu Har (1997), Assertions for Dynamic Shape Analysis of List Data Structures, AADEBUG '97, Proceedings of the Third International Workshop on Automatic Debugging, Linköping Electronic Articles in Computer and Information Science, Linköping University, с. 37—42, архів оригіналу за 16 серпня 2021, процитовано 16 серпня 2021.

Посилання

• Габріель Ніваш, Проблема виявлення циклу та алгоритм стека [Архівовано 16 серпня 2021 у Wayback Machine.]
• Черепаха і заєць [Архівовано 8 червня 2021 у Wayback Machine.], Портлендське сховище візерунків
• Алгоритм виявлення циклу Флойда (Черепаха і заєць)
• Алгоритм виявлення циклу Брента (Телепортуюча черепаха)