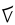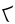|
Кактовикские цифры Кактовикские цифры — система записи для используемой инупиатами Аляски двадцатеричной системы счисления. Основание 20 в системе счисления используется во всех эскимосско-алеутских языках, и в том числе в инупиатском, при этом используется пятеричная база[англ.], то есть счёт ведётся с промежуточными отсчётами в точках 5, 10 и 15[1]. Арабские цифры, которые были разработаны для десятичной системы счисления, не подходят для языков инуитов. Чтобы решить эту проблему, учащиеся, живущие в городе Кактовик на Аляске, в 1994 году изобрели систему записи чисел[2], которая распространилась среди инупиатов[3]. Кактовикские цифры наглядно отражают лексическую структуру системы счисления народа инупиак. Например, число 7 на инупиаке называется tallimat malġuk («пять-два»), а кактовикская цифра для семи — это верхний штрих (пять), соединённый с двумя нижними штрихами (два): ЗначенияВ таблице представлены десятичные значения кактовикских чисел до трёх знаков слева и справа от места единиц[4].
Происхождение В начале 1990-х годов во время дополнительных занятий по математике в школе Гарольда Кавеолука в Кактовике[2] ученики отметили, что в их языке используется двадцатеричная система счисления, и обнаружили, что с ними нельзя выполнять арифметические операции, так как арабские цифры не имеют достаточного количества символов для представления инупиакских чисел[5]. Ученики создали десять дополнительных символов, но обнаружили, что их трудно запомнить. В средней школе городка училось девять учеников. Их работой руководил учитель Уильям Бартли[5]. После мозгового штурма ученики выделили несколько качеств, которыми должна обладать идеальная система[5]:
В инупиакском языке нет слова, обозначающего ноль, и ученики решили, что кактовикская цифра 0 должна выглядеть как скрещённые руки, что означает, что ничего не считается[5]. Когда ученики начали преподавать свою новую систему младшим ученикам в школе, младшие ученики, как правило, сжимали числа, чтобы поместиться в блок такого же размера. Таким образом, они создали знаковую нотацию, в которой нижняя часть цифры 5 составляет верхнюю часть цифры, а остаток — нижнюю часть. Это оказалось визуально полезным при выполнении арифметических операций[5]. Вычисление СчётыДля своей системы счисления ученики создали счёты в школьной мастерской. Изначально они предназначались для помощи в преобразовании десятичной дроби в систему с основанием 20 и наоборот, но ученики обнаружили, что их конструкция вполне естественно поддаётся арифметике с основанием 20. В верхней части их счётов было по три костяшки в каждом столбце для значений подосновы 5, а в нижней секции было по четыре костяшки в каждом столбце для остальных единиц[5]. Арифметика.svg)   (красный) входит в первые две цифры делимого один раз (синий) и один раз в частном (синий). Он умещается в следующие две цифры (подчёркнуты) один раз, но повёрнут (красный), поэтому следующая цифра в частном повёрнута на единицу (пять — красный). Последние две цифры совпадают один раз для получения последней в частном (белый)..svg)   входит в первые три цифры делимого дважды (обведены красным и синим), для двух в частном (красный и синий), в следующие три разряда (зелёный), не входит в следующие (ноль в частном), а в оставшиеся белые цифры один раз.Учащиеся обнаружили преимущество своей новой системы в том, что вычисления стали проще, чем с арабскими цифрами[5]. Сложение двух цифр будет выглядеть как их сумма. Например,
в кактовикской системе
Вычитать ещё проще: нужно убрать необходимое количество штрихов, чтобы получить ответ[5]. Ещё одним преимуществом стало деление в длину. Визуальные аспекты и подоснова из пяти сделали деление больших чисел почти таким же простым, как деление коротких, поскольку не требовали записи в подтаблицах для умножения и вычитания промежуточных шагов[2]. Учащиеся могли отслеживать штрихи промежуточных шагов цветными карандашами в сложной системе разбиения на части[5]. РаспространениеКактовикские цифры получили широкое распространение среди инупиатов Аляски. Они были включены в программы языкового погружения и помогли возродить счёт по основанию 20, который выходил из употребления среди инупиатов из-за преобладания системы с основанием 10 в школах с английским языком обучения[2][5]. В 1995 году ученики средней школы Кактовика, которые изобрели эту систему, поступили в среднюю школу в Барроу (Аляска). Им разрешили преподавать эту систему ученикам местной средней школы, а местный колледж Игисавик добавил в свою учебную программу курс математики инуитов[5]. В 1996 году комиссия по истории, языку и культуре инуитов официально признала кактовикскую систему, а в 1998 году Совет инуитов в Канаде рекомендовал разработать и использовать эти числительные в своей стране[3]. ЗначениеРезультаты Калифорнийского теста на успеваемость по математике в средней школе Кактовика в 1997 году резко улучшились по сравнению с предыдущими годами. После введения новых цифр их оценки стали выше средних по стране. Предполагается, что способность работать как десятичной, так и с двадцатеричной системами может дать заметные преимущества тем ученикам, которые имеют два образа мышления о мире[5]. Разработка собственной системы счисления помогает продемонстрировать учащимся из Аляски, что математика встроена в их культуру и язык, а не в западную культуру. Это отход от ранее распространённого мнения о том, что математика есть просто необходимость для поступления в колледж. Студенты-иностранцы могут увидеть практический пример иного мировоззрения, часть этноматематики[6]. КодировкаКактовикским цифрам присвоен блок в дополнительной многоязычной плоскости Unicode (U + 1D2C0-1D2DF)[7]. Эти изменения были приняты Техническим комитетом Unicode в апреле 2021 года и будут опубликованы как часть Unicode 15 в 2022 году. Они занимают диапазон от U + 1D2C0 (кактовикская цифра 0) до U + 1D2D3 (кактовикская цифра 19).
Примечания
Ссылки
|
