|
Граф МакГи
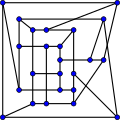
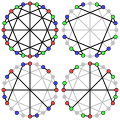
В теории графов графом МакГи, или (3-7)-клеткой, называется 3-регулярный граф с 24 вершинами и 36 рёбрами.[1] Граф МакГи — это единственная (3,7)-клетка (наименьший кубический с обхватом 7). Он является наименьшей кубической клеткой, не являющейся графом Мура. Впервые открытый Хорстом Саксом[англ.], но не опубликованный[2], граф назван в честь МакГи (W. F. McGee), который опубликовал результат в 1960 году[3]. Позднее, в 1966 году, Уильям Томас Татт доказал, что это единственная (3,7)-клетка[4][5][6]. Известны наименьшие кубические графы с числом скрещиваний 1—8 (последовательность A110507 в OEIS), наименьший граф с числом скрещиваний 8 — это граф МакГи. Существует 5 неизоморфных кубических графов порядка 24 с числом скрещиваний 8[7], один из них — обобщённый граф Петерсена G(12,5), известный также как Граф Науру[8]. Граф МакГи имеет радиус 4, диаметр 4, хроматическое число 3 и хроматический индекс 3. Он также 3-вершинно-связен и 3-рёберно-связен. Алгебраические свойстваХарактеристический многочлен графа МакГи равен . Автоморфизм группы графа МакГи имеет порядок 32 и не транзитивен относительно вершин — имеется две орбиты вершин длины 8 и 16. Граф МакГи — это наименьшая кубическая клетка, не являющаяся вершинно-транзитивной[9]. Галерея
Примечания
|
||||||||||||||||||||||||||||