pt NP-dif%C3%ADcil

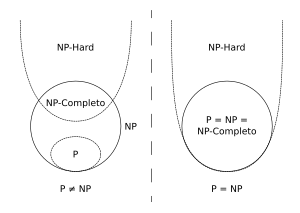NP-difícil (ou NP-hard, ou NP-complexo) na teoria da complexidade computacional, é uma classe de problemas que são, informalmente, "Pelo menos tão difíceis quanto os problemas mais difíceis em NP". Um problema H é NP-difícil se e somente se (sse) existe um problema NP-completo L que é Turing-redutível em tempo polinomial para H (i.e., L?=?_TH). Em outras palavras, L pode ser resolvido em tempo polinomial por uma Máquina de Turing não determinística com um oráculo para H. Informalmente, podemos pensar em um algoritmo que pode chamar tal Máquina de Turing Não-Determinística como uma sub-rotina para resolver H, e resolver L em tempo polinomial, se a chamada da sub-rotina leva apenas um passo para computar. Problemas NP-difíceis podem ser de qualquer tipo: problemas de decisão, problemas de pesquisa ou problemas de otimização.

Como conseqüências da definição, temos que (note que estas afirmações não são definições):

O problema H é pelo menos tão difícil quanto L, porque H pode ser usado para resolver L;
Como L é NP-completo e, portanto, o mais difícil na classe NP, também o problema H é pelo menos tão difícil quanto um NP, mas H não tem que estar em NP e, consequentemente, não tem de ser um problema de decisão (mesmo que seja um problema de decisão, ele não precisa estar em NP);
Uma vez que os problemas NP-completos transformam-se uns aos outros por redução um-para-muitos em tempo polinomial (também chamada de transformação polinomial), todos os problemas NP-completos podem ser resolvidos em tempo polinomial por uma redução para H, Assim, todos os problemas em NP reduzem para H; note-se, porém, que isso envolve a combinação de duas transformações diferentes: de problemas de decisão NP-completos para o problema NP-completo L por transformação polinomial, e de L para H pela redução em tempo polinomial de Turing;
Se existe um algoritmo polinomial para qualquer problema NP-difícil, então existem algoritmos polinomiais para todos os problemas em NP, e, portanto, P = NP;
Se P != NP, então os problemas NP-difíceis não têm soluções em tempo polinomial, uma vez que P = NP não resolve se os problemas NP-difíceis podem ser resolvidos em tempo polinomial;
Se um problema de otimização H tem uma versão de decisão NP-completo L, então H é NP-difícil.

Um erro comum é pensar que NP em NP-difícil representa não-polinomial. Embora seja amplamente suspeito de que não existem algoritmos de tempo polinomial para problemas NP-difíceis, isto nunca foi provado. Além disso, a classe NP contém também todos os problemas que podem ser resolvidos em tempo polinomial.

Exemplos

Um exemplo de um problema NP-difícil é o problema de decisão da soma de subconjuntos, que é o seguinte: dado um conjunto de números inteiros, pode algum subconjunto não-vazio deste somar zero? Isso é uma questão do tipo sim/não, e acontece de ser NP-completo. Outro exemplo de um problema NP-difícil é o problema de otimização de se encontrar a rota de menor custo através de todos os nós de um grafo ponderado. Isto é comumente conhecido como o Problema do caixeiro viajante.

Há também problemas de decisão que são NP-difíceis, mas não NP-completos, por exemplo, o problema da parada. Este é o problema que pergunta se "dado um programa e dada a sua entrada, ele irá executar para sempre?" Esta é uma questão do tipo sim/não, por isso este é um problema de decisão. É fácil provar que o problema da parada é NP-difícil, mas não NP-completo. Por exemplo, o problema de satisfatibilidade booleana pode ser reduzido ao problema da parada, transformando-o em uma descrição de uma máquina de Turing que tenta todos as atribuições verdadeiras e quando encontra uma que satisfaça a fórmula, ela para, caso contrário, entra em um loop infinito. Também é fácil ver que o problema da parada não está na classe NP já que todos os problemas em NP são decidíveis em um número finito de operações, enquanto o problema da parada, em geral, não é. Há também problemas NP-difíceis que não são NP-completos nem indecidíveis.

Definições alternativas

Uma definição alternativa de NP-difícil que é usada frequentemente restringe os problemas NP-difíceis aos problemas de decisão e, em seguida, usa redução de muitos para um, de tempo polinomial, ao invés da redução de Turing. Assim, formalmente, uma linguagem L é NP-difícil se ?L^'???NP, L^'?=?L. Se for o caso que L está em NP, então L é chamada NP-completo.

Convenção de nomeação NP

O sistema de nomeação da família NP é confuso: os problemas NP-difíceis, não são todos NP, a despeito de ter NP como o prefixo do seu nome da classe. No entanto, os nomes estão agora estabelecidos e improváveis de mudar. Por outro lado, o sistema de nomeação NP- tem algum sentido mais profundo, porque a família NP é definida em relação à classe NP:

NP-difícil: Tão difíceis quanto os problemas mais difíceis em NP. Tais problemas não precisam estar em NP, na verdade, eles nem precisam ser obrigatoriamente problemas de decisão.
NP-completo: Estes são os problemas mais difíceis em NP. Tais problemas são NP-difíceis e em NP.
NP-fácil: Na maioria tão difíceis quanto NP, mas não necessariamente em NP, uma vez que podem não ser problemas de decisão.
NP-equivalente: Exatamente tão difícil quanto os problemas mais difíceis em NP, mas não necessariamente em NP.