Fenômeno de Gibbs

Aproximação da Série de Fourier

Em matemática, o fenômeno de Gibbs, descoberto por Henry Wilbraham[1] e redescoberto por J. Willard Gibbs,[2] é a forma peculiar que as séries de Fourier de funções periódicas de partes continuamente diferenciáveis tomam em pontos de descontinuidade de salto. A n-ésima soma parcial da série de Fourier oscila bastante perto do salto, o que pode fazer aumentar o valor máximo da soma parcial acima do valor da própria função original.[3] Esse tipo de comportamento já tinha sido observado por físicos experimentais, mas acreditava-se que devia-se a imperfeições nos aparelhos de medição.[4]

Ao fazer uma convergência das somas parciais finitas da Série de Fourier de uma função encontra-se oscilações cujas amplitudes não convergem para zero. Isso se dá em razão da dificuldade de aproximar funções descontínuas a finitas séries de ondas senos e cossenos.[5]

Descrição

O fenômeno de Gibbs ocorre quando representa-se uma função por Série de Fourier, a qual possui um número finito de descontinuidades em seu período. Tal fenômeno envolve o fato de que ocorre uma ultrapassagem nos saltos dessas descontinuidades não desaparecem a medida que ocorre a adição de mais termos na soma parcial.Como pode ser visto nas representações a direita, conforme o número de termos aumenta, o erro da aproximação é reduzido em largura e energia, contudo converge para uma altura fixa.

Aproximação da função de onda quadrada usando 5 harmônicos

As três fotos na direita demonstram o fenômeno de Gibbs para o tipo de onda quadrada (no caso de altura ${\displaystyle \pi /4}$), as quais possuem expansão:

${\displaystyle \operatorname {sen}(x)+1/3\centerdot \operatorname {sen}(3x)+1/5\centerdot \operatorname {sen}(5x)...}$

Mais precisamente, esta onda quadrada tem salto de descontinuidade de tamanho ${\displaystyle \pi /4}$ para cada número inteiro múltiplo de ${\displaystyle \pi }$.

Pode ser calculado uma formula explicita para o erro da altura limite da onda quadrada. Obtém-se assim que a Série de Fourier excede a altura de ${\displaystyle \pi /4}$ da onda por:

Aproximação da função de onda quadrada usando 25 harmônicos

${\displaystyle 1/2\centerdot \int \limits _{0}^{\pi }(\operatorname {sen}(t)/t)dt-\pi /4=\pi /2\centerdot (0.089489872236...)}$

Ou aproximadamente 9% do salto. Mais especificamente, em qualquer salto de uma função por partes continuamente diferenciável com um salto de altura α, a n-ésima  série de Fourier parcial vai ultrapassar esta altura por aproximadamente:

${\displaystyle a\centerdot (0.089489872236...)}$

No local de descontinuidade, a Série de Fourier parcial vai convergir para o ponto mediano do salto (independentemente do valor original da função neste ponto). Ou seja, através da definição que a oscilação da soma parcial de ordem n no ponto ${\displaystyle x=p}$ como:

${\displaystyle \omega _{n}(S_{n},p)=maxS_{n}(f)-minS_{n}(f)}$

Gibbs foi capaz de observar que o valor desta oscilação não se aproxima do salto de ${\displaystyle f}$ no ponto ${\displaystyle x=p}$, independente do grau de proximidade de ${\displaystyle x}$ com ${\displaystyle p}$.

Na verdade, a soma parcial da série de Fourier ultrapassa o valor limite da função à direita e tem valor menor do que a função. Esta é uma forma natural de compensar o salto que a soma parcial realizará.[6]

História

O Fenômeno de Gibbs foi notado e analisado pela primeira vez por Henry Wilbraham em um artigo de 1848.[7] O artigo não chamou muita atenção até 1914 quando foi mencionado em um estudo de Heinrich Burkhardt sobre análise matemática na enciclopédia de Klein.[8] Em 1898, Albert A. Michelson desenvolveu um dispositivo que computava e ressintetizava a série de Fourier.[9][10] Há um mito que diz que quando eram colocados os coeficientes da Fourier para uma onda quadrada na máquina, o gráfico oscilava nas descontinuidades e isso ocorria pois ele era um dispositivo físico sujeito a erros de confecção. De fato os gráficos produzidos pela máquina não eram bons o suficiente para exibir o Fenômeno de Gibbs claramente, e Michelson pode não ter percebido isto, uma vez que ele não mencionou sobre esse efeito em seu artigo (Michelson & Stratton 1898) sobre sua máquina ou em suas cartas à revista Nature.[1] Inspirado em uma correspondência da Nature entre Michelson e Love sobre a convergência da série de Fourier da funcão da onda quadrada, em 1898 J. Willard Gibbs publicou uma pequena nota na qual ele considerou o que hoje se chama onda dente de serra e apontou a importante distinção entre o limite do gráficos das somas parciais da série de Fourier e o gráfico da função que é o limite dessas somas parciais. Na sua primeira carta, Gibbs não percebeu o Fenômeno de Gibbs, e o limite que ele descreveu para os gráficos das somas parciais era impreciso. Em 1899, ele publicou uma correção na qual ele descreveu a ultrapassagem do ponto de descontinuidade (Nature: Abril 27, 1899, p. 606). Em 1906, Maxime Bôcher forneceu uma análise matemática detalhada sobre essa ultrapassagem, criando o termo "Fenômeno de Gibbs"[11] e tornando ele popular.[1]

Depois que a existência do artigo de Henry Wilbraham se tornou conhecida, em 1925 Horatio Scott Carslaw comentou "Nós podemos ainda chamar essa propriedade da série de Fourier (e de certas outras séries) de Fenômeno de Gibbs, porém nós não podemos mais declarar que essa propriedade foi primeiramente descoberta por Gibbs".[12]

Explicação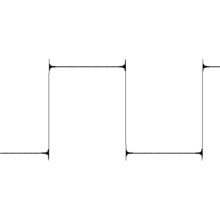

Aproximação da função de onda quadrada usando 125 harmônicos

Informalmente, o fenômeno de Gibbs reflete a dificuldade inerente a aproximação uma função descontínua por uma série finita de senos e cossenos contínuos. É importante colocar um ênfase na palavra finito porque apesar de toda soma parcial da série de Fourier ultrapassa a função que está aproximando, o limite da soma parcial não ultrapassa. O valor de x para a qual a maior ultrapassagem é alcançada move-se cada vez mais perto da descontinuidade conforme aumentam o número de termos somados, portanto mais uma vez informalmente, uma vez que a ultrapassagem foi passada por um valor de x particular, a convergência para tal valor se torna possível.

Para uma função por partes a série de Fourier converge para a função em todos os pontos exceto em um salto de descontinuidade. Nos próprios saltos de descontinuidades, para a função por partes, ira convergir para a média aritmética dos limites laterais da função original. Isto é uma consequência do teorema de Dirichlet.[13]

O fenômeno de Gibbs também pode ser relacionado ao princípio o qual os decaimentos dos coeficientes de Fourier de uma função no infinito são controlados pela suavidade da função em questão; funções muito suaves vão ter ou decaimento mais abrupto dos coeficientes de Fourier (resultando em uma rápida convergência da série de Fourier), enquanto que uma função descontinua vai ter um decaimento muito mais retardado dos coeficientes de Fourier (causando uma lenta convergência à série de Fourier). Note por exemplo que os coeficientes de Fourier 1, -1/3, 1/5 ... da onda quadrada descontinua, ilustrada acima, decai tão rápido quanto as séries harmônicas, as quais não são absolutamente convergentes; de fato, a série de Fourier acima se mostra ser somente condicionalmente convergente para quase todo valor de x. Isso fornece uma explicação parcial para o fenômeno de Gibbs, já que a série de Fourier com coeficientes de Fourier absolutamente convergentes seria uniformemente convergente pelo teste M de Weierstrass e seria portanto, incapaz de apresentar o comportamento oscilatório exibido acima. Pela mesma razão, é impossível para funções descontinuas terem uma convergência absoluta de seus coeficientes de Fourier, uma vez que a função seria o limite uniforme de funções continuas e portanto seria continua, o que é uma contradição.

Tratamento

Em prática, as dificuldades associadas com o fenômeno de Gibbs podem ser melhoradas pelo uso do método de suavização da série de Fourier, assim como soma de Fejér ou a soma de Riesz, ou pelo uso de aproximações sigma. Usando a transformada continua de wavelet, o fenômeno wavelet Gibbs nunca excede o fenômeno de Gibbs.[14] Também, usando a transformada discreta de wavelet com funções bases de Haar, realmente, o fenômeno de Gibbs não ocorre no caso de dados contínuos em um salto de descontinuidade,[15] e é mínimo no caso discreto com grandes mudanças de pontos. Na análise de wavelet, isto é comumente referido como o fenômeno de Longo.

Descrição matemática formal do fenômeno

Seja ${\displaystyle f:{\mathbb {R} }\to {\mathbb {R} }}$ uma função contínua por partes e periódica com período ${\displaystyle L>0}$. Supõe-se que em um ponto ${\displaystyle x_{0}}$ o limite lateral à esquerda ${\displaystyle f(x_{0}^{-})}$ e o limite lateral à direita ${\displaystyle f(x_{0}^{+})}$ da função ${\displaystyle f}$ diferem de um valor diferente de zero igual a ${\displaystyle a}$:

${\displaystyle f(x_{0}^{+})-f(x_{0}^{-})=a\neq 0.}$

Fenômeno de Gibbs para várias aproximações.

Para cada valor inteiro positivo N ≥ 1, seja S_N fa a N-ésima Série de Fourier parcial

${\displaystyle S_{N}f(x):=\sum _{-N\leq n\leq N}{\hat {f}}(n)e^{\frac {2i\pi nx}{L}}={\frac {1}{2}}a_{0}+\sum _{n=1}^{N}\left(a_{n}\cos \left({\frac {2\pi nx}{L}}\right)+b_{n}\sin \left({\frac {2\pi nx}{L}}\right)\right),}$

onde os coeficientes de Fourier ${\displaystyle {\hat {f}}(n),a_{n},b_{n}}$ são dados pela fórmula usual

${\displaystyle {\hat {f}}(n):={\frac {1}{L}}\int _{0}^{L}f(x)e^{-2i\pi nx/L}\,dx}$

${\displaystyle a_{n}:={\frac {2}{L}}\int _{0}^{L}f(x)\cos \left({\frac {2\pi nx}{L}}\right)\,dx}$

${\displaystyle b_{n}:={\frac {2}{L}}\int _{0}^{L}f(x)\sin \left({\frac {2\pi nx}{L}}\right)\,dx.}$

então tem-se que

${\displaystyle \lim _{N\to \infty }S_{N}f\left(x_{0}+{\frac {L}{2N}}\right)=f(x_{0}^{+})+a\cdot (0.089392\dots )}$

e

${\displaystyle \lim _{N\to \infty }S_{N}f\left(x_{0}-{\frac {L}{2N}}\right)=f(x_{0}^{-})-a\cdot (0.089392\dots )}$

mas

${\displaystyle \lim _{N\to \infty }S_{N}f(x_{0})={\frac {f(x_{0}^{-})+f(x_{0}^{+})}{2}}.}$.

De maneira geral, se ${\displaystyle x_{N}}$ é uma sequência de números reais que converge para ${\displaystyle x_{0}}$ com ${\displaystyle N\to \infty }$, e se o valor ${\displaystyle a}$ é positivo então

${\displaystyle \limsup _{N\to \infty }S_{N}f(x_{N})\leq f(x_{0}^{+})+a\cdot (0.089392\dots )}$

e

${\displaystyle \liminf _{N\to \infty }S_{N}f(x_{N})\geq f(x_{0}^{-})-a\cdot (0.089392\dots ).}$.

Analogamente, se ${\displaystyle a<0}$, então é preciso trocar o limite superior e o limite inferior e, além disso, trocar os símbolos matemáticos ≤ e ≥ nas inequações acima.

Exemplo da onda quadrada

Animação da construção da onda quadrada para um numero crescente de harmônicos. O fenômeno de Gibbs é visível especialmente quando o número de harmônicos é grande

Agora se ilustra o Fenômeno de Gibbs para o caso da onda quadrada formada pela soma infinita de senos e cossenos. O período ${\displaystyle L}$ agora é igual a ${\displaystyle 2\pi }$, a descontinuidade ${\displaystyle x_{0}}$ encontra-se no zero e o salto ${\displaystyle a}$ tem valor de ${\displaystyle \pi /2}$. Por simplicidade, se trabalhará com o caso em que N é um número par (o caso para N ímpar é muito similar). Então tem-se que:

${\displaystyle S_{N}f(x)=\sin(x)+{\frac {1}{3}}\sin(3x)+\cdots +{\frac {1}{N-1}}\sin((N-1)x).}$

Substituindo ${\displaystyle x=0}$ se obtém que

${\displaystyle S_{N}f(0)=0={\frac {-{\frac {\pi }{4}}+{\frac {\pi }{4}}}{2}}={\frac {f(0^{-})+f(0^{+})}{2}}}$

Posteriormente calcula-se

${\displaystyle S_{N}f\left({\frac {2\pi }{2N}}\right)=\sin \left({\frac {\pi }{N}}\right)+{\frac {1}{3}}\sin \left({\frac {3\pi }{N}}\right)+\cdots +{\frac {1}{N-1}}\sin \left({\frac {(N-1)\pi }{N}}\right).}$

Ao introduzir a função sinc normalizada ${\displaystyle \operatorname {sinc} (x)\,}$ é possível reescrever a expressão acima como

${\displaystyle S_{N}f\left({\frac {2\pi }{2N}}\right)={\frac {\pi }{2}}\left[{\frac {2}{N}}\operatorname {sinc} \left({\frac {1}{N}}\right)+{\frac {2}{N}}\operatorname {sinc} \left({\frac {3}{N}}\right)+\cdots +{\frac {2}{N}}\operatorname {sinc} \left({\frac {(N-1)}{N}}\right)\right].}$

Mas percebe-se que a expressão em colchetes é uma aproximação por integração numérica para a integral ${\displaystyle \int _{0}^{1}\operatorname {sinc} (x)\ dx}$. Como a função sinc é contínua, essa aproximação converge para a integral apresentada com ${\displaystyle N\to \infty }$. Portanto tem-se que:

${\displaystyle {\begin{aligned}\lim _{N\to \infty }S_{N}f\left({\frac {2\pi }{2N}}\right)&={\frac {\pi }{2}}\int _{0}^{1}\operatorname {sinc} (x)\,dx\\[8pt]&={\frac {1}{2}}\int _{x=0}^{1}{\frac {\sin(\pi x)}{\pi x}}\,d(\pi x)\\[8pt]&={\frac {1}{2}}\int _{0}^{\pi }{\frac {\sin(t)}{t}}\ dt\quad =\quad {\frac {\pi }{4}}+{\frac {\pi }{2}}\cdot (0.089490\dots ),\end{aligned}}}$

Um cálculo análogo mostra que

${\displaystyle \lim _{N\to \infty }S_{N}f\left(-{\frac {2\pi }{2N}}\right)=-{\frac {\pi }{2}}\int _{0}^{1}\operatorname {sinc} (x)\ dx=-{\frac {\pi }{4}}-{\frac {\pi }{2}}\cdot (0.089490\dots ).}$.

Consequências

Em processamento de sinais, o fenômeno de Gibbs é indesejável por causar erro na leitura do sinal pelo equipamento, seja por clipping para o caso do erro atribuído aos picos do fenômeno, ou por ringing artifacts para as oscilações. Para circuitos que operam em baixas frequências, os efeitos do fenômeno podem ser reduzidos ou mesmo eliminados por meio de filtros passa-baixa.

Em imagens de ressonância magnética (IRM), o fenômeno de Gibbs causa artefato, erro de medição gerado pela ineficiência dos aparelhos empregados ou pela ineficácia do método utilizado, na presença de regiões adjacentes com acentuada diferença de sinal. Esse fenômeno é comumente encontrado em ressonâncias magnéticas que cobrem a região espinhal, em que o fenômeno de Gibbs pode simular a aparência de siringomielia.

Referências

1. Hewitt, Edwin; Hewitt, Robert E. (1979). «The Gibbs-Wilbraham phenomenon: An episode in fourier analysis». Archive for History of Exact Sciences. 21 (2): 129–160. doi:10.1007/BF00330404. Consultado em 16 de setembro de 2011  Disponível on-line em: National Chiao Tung University: Open Course Ware: Hewitt & Hewitt, 1979.^[ligação inativa]
2. Andrew Dimarogonas. Vibration for engineers. [S.l.: s.n.] ISBN 0-13-462938-8 
3. H. S. Carslaw (1930). Introduction to the theory of Fourier's series and integrals Third Edition ed. New York: Dover Publications Inc. Chapter IX 
4. Vretblad, Anders (2000), Fourier Analysis and its Applications, Graduate Texts in Mathematics 223, New York: Springer Publishing, ISBN 0-387-00836-5, Seção 4.7.
5. Notas de Aula dos Profs. Fabio Azevedo e Esequia Sauter - Análise de Fourier
6. Notas de Aula do prof. Ulysses Sodré
7. The Cambridge and Dublin Mathematical Journal (em inglês). [S.l.]: Macmillan, Barclay and Macmillan. 1848 
8. Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. [S.l.: s.n.] 1904. 1049 páginas 
9. «Albert Michelson's Harmonic Analyzer (book details))». www.engineerguy.com. Consultado em 29 de setembro de 2019 
10. Wolfram, Stephen (2002). A new kind of science. [S.l.]: Champaign, IL : Wolfram Media 
11. Bocher, Maxime (1906). «Introduction to the Theory of Fourier's Series». Annals of Mathematics. 7 (3): 81–152. ISSN 0003-486X. doi:10.2307/1967238 
12. Carslaw, H. S. (outubro de 1925). «A historical note on Gibbs' phenomenon in Fourier's series and integrals». Bulletin of the American Mathematical Society (em inglês). 31 (8): 420–424. ISSN 0002-9904 
13. M. Pinsky (2002). Introduction to Fourier Analysis and Wavelets. [S.l.: s.n.] 
14. Rasmussen, Henrik O. "The Wavelet Gibbs Phenomenon.". [S.l.: s.n.] 
15. Kelly, Susan E. "Gibbs Phenomenon for Wavelets.". [S.l.: s.n.]