|
Árvore rubro-negra
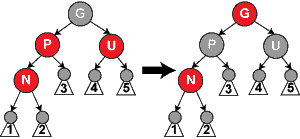
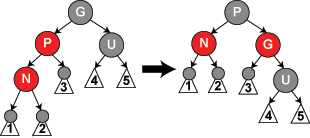
Uma árvore rubro-negra é um tipo de árvore binária de busca balanceada, uma estrutura de dados usada em ciência da computação, tipicamente para implementar vetores associativos. A estrutura original foi inventada em 1972, por Rudolf Bayer[carece de fontes] que a chamou de "Árvores Binárias B Simétricas", mas adquiriu este nome moderno em um artigo de 1978 escrito por Leonidas J. Guibas e Robert Sedgewick.[2] Ela é complexa, mas tem um bom pior-caso de tempo de execução para suas operações e é eficiente na prática: pode-se buscar, inserir, e remover em tempo O(log n), onde n é o número total de elementos da árvore. De maneira simplificada, uma árvore rubro-negra é uma árvore de busca binária que insere e remove de forma inteligente, para assegurar que a árvore permaneça aproximadamente balanceada. TerminologiaUma árvore rubro-negra é um tipo especial de árvore binária, usada em ciência da computação para organizar dados que possam ser comparáveis. Nas árvores rubro-negras, os nós folhas não são relevantes e não contém dados. Estas folhas não precisam ser mantidas em memória de computador - basta apenas um ponteiro para nulo para identificá-las — mas algumas operações em árvores rubro-negras são simplificadas se os nós folha forem explicitados. Para economizar memória, algumas vezes um nó sentinela interpreta o papel de todos os nós folha; todas as referências dos nós internos para os nós folha apontam para o nó sentinela. Árvores rubro-negras, como todas as árvores binárias de busca, permitem travessia em-ordem de elementos de maneira eficiente, pois é possível acessar o pai de qualquer nó. O tempo de busca resulta da travessia da raiz a folha, desta forma uma árvore balanceada, tendo a menor altura possível, resulta em tempo de busca O(log n). Propriedades Uma árvore rubro-negra é uma árvore de busca binária onde cada nó tem um atributo de cor, vermelho ou preto. Além dos requisitos ordinários impostos pelas árvores de busca binárias, as árvores rubro-negras tem os seguintes requisitos adicionais:
Essas regras asseguram uma propriedade crítica das árvores rubro-negras: que o caminho mais longo da raiz a qualquer folha não seja mais do que duas vezes o caminho mais curto da raiz a qualquer outra folha naquela árvore. O resultado é que a árvore é aproximadamente balanceada. Como as operações de inserção, remoção, e busca de valores necessitam de tempo de pior caso proporcional à altura da árvore, este limite proporcional a altura permite que árvores rubro-negras sejam eficientes no pior caso, diferentemente de árvore de busca binária. Para perceber por que essas propriedades garantem isto, basta observar que nenhum caminho pode ter dois nós vermelhos sucessivos, devido à propriedade 4. O caminho mais curto possível tem todos os nós pretos, e o caminho mais longo possível alterna entre nós vermelhos e pretos. Desde que todos os caminhos máximos têm o mesmo número de nós pretos, pela propriedade 5, isto mostra que nenhum caminho é mais do que duas vezes mais longo que qualquer outro caminho. Em muitas das representações de estruturas de dados em árvore, é possível para um nó pai ter só um filho, e os nós folha contêm dados. É possível representar árvores rubro-negras neste paradigma, mas ele modifica várias propriedades e deixa os algoritmos mais complexos. Por essa razão, este artigo usa "folhas nulas", que não contêm nenhum dado e simplesmente servem para indicar onde a árvore termina, como mostrado acima. Esses nós muitas vezes são omitidos dos desenhos, resultando em uma árvore que parece contradizer os princípios acima mencionados, mas que de fato não faz. Uma conseqüência disto é que todo nó interno (não-folha) têm dois filhos, embora um ou ambos filhos possam ser folhas nulas. Alguns explicam uma árvore rubro-negra como uma árvore de busca binária cujas bordas, em vez de nós, são coloridas em vermelho ou preto, mas isto não faz nenhuma diferença. A cor de um nó na terminologia deste artigo corresponde à cor da borda que une o nó ao seu pai, exceto que o nó de raiz é sempre preto (propriedade 2) ao passo que a borda correspondente não existe. Analogia com árvores B de ordem 4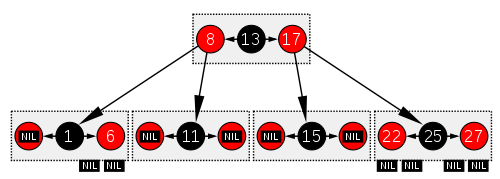 Uma árvore rubro-negra tem estrutura similar a uma árvore B de ordem 4, onde cada nó pode conter de 1 até 3 valores e (consequentemente) entre 2 e 4 ponteiros para filhos. Nesta árvore B, cada nó contem apenas um valor associado ao valor de um nó negro da árvore rubro-negra, com um valor opcional antes e/ou depois dele no mesmo nó. Estes valores opcionais são equivalentes a um nós vermelhos na árvore rubro-negra. Uma maneira de visualizar esta equivalência é "subir" com os nós vermelhos na representação gráfica da árvore rubro-negra de modo a alinhá-los horizontalmente com seus pais negros, assim criando uma lista de nós na horizontal. Tanto na árvore B quanto na representação modificada da árvore rubro-negra, todos as folhas estão no mesmo nível. Entretanto, esta árvore B é mais geral que uma árvore rubro-negra, já que a árvore B pode ser convertida de mais de uma maneira em uma árvore rubro-negra. Se a lista de valores de um nó da árvore B contém somente 1 valor, então esse valor corresponde a um nó negro com dois filhos. Se a lista contém 3 valores, então o valor central corresponde a um nó negro e os outros dois valores correspondem a filhos vermelhos. Se a lista contém 2 valores, então podemos fazer qualquer um dos valores negro e o outro valor corresponde a seu filho vermelho. OperaçõesAs operações somente-leitura em uma árvore rubro-negra não necessitam nenhuma modificação daquelas usadas em uma árvore binária, porque toda árvore rubro-negra é um caso especial de uma árvore de busca binária simples. Contudo, o resultado imediato de uma inserção ou remoção pode violar as propriedades de uma árvore rubro-negra. Restaurar as propriedades rubro-negras requer um pequeno número (O(log n) ou O(1)) de modificações de cores (que na prática são muito rápidas) e não mais do que três rotações de árvore (duas para a inserção). Embora operações de inserção e remoção sejam complicadas, seus tempos permanecem O(log n). InserçãoA cada vez que uma operação é realizada na árvore, testa-se este conjunto de propriedades e são efetuadas rotações e ajuste de cores até que a árvore satisfaça todas estas regras. Uma rotação é uma operação realizada na árvore para garantir seu balanceamento. A rotação na árvore rubro-negra pode ser feita à direita e à esquerda, onde são alterados os ponteiros dos nós rotacionados. Ao inserir-se um elemento em uma árvore rubro-negra, esta é comparada com os elementos e alocada em sua posição conforme a regra 2. Ao inserir-se um elemento ele é sempre da cor vermelha (exceto se for o nó raiz). A seguir a árvore analisa o antecessor da folha. Se este for vermelho será necessário alterar as cores para garantir a regra 4. Uma inserção começa pela adição de um nó de forma semelhante a uma inserção em árvore binária, pintando-se o nó em vermelho. Diferentemente de uma árvore binária onde sempre adicionamos uma folha, na árvore rubro-negra as folhas não contém informação, então inserimos um nó vermelho na parte interna da árvore, com dois nós filhos pretos, no lugar de uma folha preta. O que acontece a seguir depende da cor dos nós vizinhos. O termo nó tio será usado para referenciar o irmão de um nó pái, como em uma árvore genealógica. Note que a:
Cada caso será demonstrado com exemplos em código C (acima) e em Java (abaixo). O tio e o avô de um nó podem ser encontrados pelas seguintes funções: Em C: struct node *
avo(struct node *n)
{
if ((n != NULL) && (n->pai != NULL))
return n->pai->pai;
else
return NULL;
}
struct node *
tio(struct node *n)
{
struct node *g = avo(n);
if (g == NULL)
return NULL; // Não ter avô significa não ter tio
if (n->pai == g->esquerda)
return g->direita;
else
return g->esquerda;
}
Em Java: public Node avo(Node n) {
if (n.getParent() == null) {
return null; // Nao ter pai significa nao ter avo
}
Node pai = n.getParent();
return pai.getParent(); // Se o pai tiver pai, retorna-o. Caso contrario, o
// retorno do metodo getParent sera null, e o retorno será null.
}
public Node tio(Node n) {
Node avo = avo(n);
if (avo == null) {
return null;
}
Node pai = n.getParent();
// Nao existe como saber se o pai eh maior ou menor que o avo, entao
// para recuperar o tio, comparamos os dois.
if (pai.compareTo(avo) > 0) { // Se pai > avo
return avo.getLeft(); // retorna o filho da esquerda, que eh menor.
// Caso nao exista, retorna null.
} else { // Se pai < avo
return avo.getRight(); // retorna o filho da direita, que eh maior.
// Caso nao exista, retorna null.
}
}
Caso 1: O novo nó N está na raiz da árvore. Neste caso, este nó é repintado de preto para satisfazer a Propriedade 2. Como esta ação adiciona um nó preto em todos os caminhos da árvore de uma só vez, a Propriedade 5 não é violada. Em C: void
insercao_caso1(struct node *n)
{
if (n->pai == NULL)
n->cor = PRETA;
else
insercao_caso2(n);
}
Em Java: public void fixCase1(Node n) {
if (n.getParent() == null) { // Se o no for raiz, pinta de preto.
n.setColor(Color.BLACK);
} else { // Se nao for, parte para o caso 2.
fixCase2(n);
}
}
Caso 2: O pai do novo nó P é preto. Neste caso a Propriedade 2 claramente não é invalidada. A Propriedade 4 tampouco é ameaçada pois o novo nó N tem como filhos dois nós-folha pretos, e sendo N vermelho, os caminhos passando por cada um dos seus filhos têm o mesmo número de nós pretos - da mesma forma que os caminhos que passavam pelo nó-folha preto que foi substituído por N. Por fim, neste caso, a árvore continua válida após a inserção, não sendo necessária mais alterações. Em C: void
insercao_caso2(struct node *n)
{
if (n->pai->cor == PRETA)
return; /* Árvore ainda é válida */
else
insercao_caso3(n);
}
Em Java: public void fixCase2(Node n) {
Color corDoPai = n.getParent().getColor();
if (corDoPai.equals(Color.RED) { // Se o pai tiver cor vermelha, parte
fixCase3(n); // para o caso 3. Se nao, a arvore esta correta.
}
}
Em C: void
insercao_caso3(struct node *n)
{
struct node *u = tio(n), *g;
if ((u != NULL) && (u->cor == VERMELHA)) {
n->pai->cor = PRETA;
u->cor = PRETA;
g = avo(n);
g->cor = VERMELHA;
insercao_caso1(g);
} else {
insercao_caso4(n);
}
}
Em Java: public void fixCase3(Node n) {
// So se chega a este metodo se o pai do no for vermelho.
// Verificaremos agora se o tio dele tambem eh vermelho.
Node tio = tio(n); // Caso nao exista tio, a variavel recebe null.
if (tio != null && tio.getColor().equals(Color.RED)) {
// se existe tio e ele eh vermelho:
// pinta o pai e o tio de preto, o avo de vermelho e roda o fixcase1 no
// avo para fazer os ajustes, caso estes sejam necessarios.
Node pai = n.getParent();
pai.setColor(Color.BLACK);
tio.setColor(Color.BLACK);
Node avo = avo(n);
avo.setColor(Color.RED);
fixCase1(avo);
} else {
fixCase4(n); // Caso nao haja tio ou ele seja preto, parte ao caso 4.
}
}
Em C: void
insercao_caso4(struct node *n)
{
struct node *g = avo(n);
if ((n == n->pai->direita) && (n->pai == g->esquerda)) {
rotacionar_esquerda(n->pai);
n = n->esquerda;
} else if ((n == n->pai->esquerda) && (n->pai == g->direita)) {
rotacionar_direita(n->pai);
n = n->direita;
}
insercao_caso5(n);
}
Em Java: public void fixCase4(Node n) {
Node pai = n.getParent();
Node avo = avo.getParent();
if (n.compareTo(pai) > 0 && pai.compareTo(avo) < 0) {
// Se o no eh filho da direita e o pai eh filho da esquerda
rotaciona_esquerda(pai);
n = n.getLeft(); // o no passa a ser o seu filho da esquerda, que
// antes da rotacao era o seu pai.
} else if (n.compareTo(pai) < 0 && pai.compareTo(avo) > 0) {
// Se o no eh filho da esquerda e o pai eh filho da direita
rotaciona_direita(pai);
n = n.getRight(); // o no passa a ser o seu filho da direita, que
// antes da rotacao era o seu pai.
}
fixCase5(n);
}
Em C: void
insercao_caso5(struct node *n)
{
struct node *g = avo(n);
n->pai->cor = PRETA;
g->cor = VERMELHA;
if ((n == n->pai->esquerda) && (n->pai == g->esquerda)) {
rotacionar_direita(g);
} else {
/*
* Aqui, (n == n->pai->direita) && (n->pai == g->direita).
*/
rotacionar_esquerda(g);
}
}
Em Java: public void fixCase5(Node n) {
Node avo = avo(n);
Node tio = tio(n);
Node pai = n.getParent();
// pinta o pai de preto e o avo de vermelho
avo.setColor(Color.RED);
pai.setColor(Color.BLACK);
if (n.compareTo(pai) < 0 && pai.compareTo(avo) < 0) {
// se o no eh filho da esquerda e o pai tambem,
// rotaciona o avo a direita.
rotaciona_direita(avo);
} else {
// se nao, quer dizer que o no eh filho da direita e o pai tambem,
// e rotacionamos o avo a esquerda.
rotaciona_esquerda(avo);
}
}
Note que a inserção é in-place, já que todas as chamadas acima são recursivas. RemoçãoA remoção nas árvores rubro-negras se inicia com uma etapa de busca e remoção como nas árvores binárias de busca convencionais. Então se alguma propriedade vermelho-preta for violada, a árvore deve ser rebalanceada. Caso a remoção efetiva seja de um nó vermelho, esta é realizada sem problemas, pois todas as propriedades da árvore se manterão intactas. Se o nó a ser removido for preto, a quantidade de nós pretos em pelo menos um dos caminhos da árvore foi alterado, o que implica que algumas operações de rotação e/ou alteração de cor sejam feitas para manter o balanceamento da árvore. Para ocorrer a remoção de um nó em arvore preta e vermelha é necessário que esse nó tenha no máximo um filho que não seja folha, a maior preocupação na remoção está em não quebrar as regras básicas que fazem uma arvore ser preta e vermelha e falando principalmente sobre a regra da altura preta. O primeiro caso verifica se o pai do nó não é nulo, se for vai para o segundo caso. No segundo caso, se o nó e seu pai forem pretos e seu irmão for vermelho o pai deve ser pintado de vermelho e o irmão de preto e então se o nó for filho esquerdo, faz a rotação à esquerda de seu pai e vai pro próximo caso, se for filho direito, rotaciona o pai à direita e vai pro próximo caso. Nesse caso, se o pai do nó, o irmão, o filho esquerdo e direito do irmão forem todos pretos, pinta o irmão de vermelho e volte para o primeiro caso com o pai do nó, se não forem vai pro próximo caso. No quarto caso, se o irmão e o filho esquerdo e direito do irmão forem pretos e o pai do nó for vermelho, deve pintar o irmão de vermelho e o pai do nó de preto, se não deve prosseguir para o próximo caso. No quinto caso, se o nó for filho esquerdo e o filho direito do irmão for preto deverá pintar o irmão de vermelho e o filho esquerdo do irmão de preto e aí sim rotacionar à direita o irmão, mas se o nó for filho direito deverá pintar o irmão de vermelho e o filho direito do irmão de preto e então rotacionar para esquerda o irmão, indo para o último caso. Ao chegar no último caso deverá pintar o pai do nó de preto, caso o nó seja filho esquerdo, pinta o filho direito do irmão do nó de preto e rotaciona o pai do nó para a esquerda, se o nó for filho direito, pinta o filho esquerdo do irmão de preto e rotaciona o pai para direita. Ao sair do encadeamento de casos poderá ser feita a remoção do nó naturalmente. O algoritmo de remoção é O(log n). Define-se para Árvores Rubro-Negras dois tipos de remoção:
Altura de um nó A altura de um nó nas árvores rubro-negras é calculada através da quantidade de nós pretos que o caminho entre o nó e sua folha descendente possui, como por invariante os caminhos traçados a partir de um nó até suas folhas descendentes devem possuir a mesma quantidade de nós pretos, esses serão sua altura. Para calcular-se a altura de um nó, existem duas formas possíveis:
 Nota: A altura de um nó será sempre a maior altura preta possível. Em C++: private: int altura(NO *atual) {
if(atual == NULL || (atual->esq == NULL && atual->dir == NULL))
return 0;
else {
if (altura(atual->esq) > altura(atual->dir))
return ( 1 + altura(atual->esq) );
else
return ( 1 + altura(atual->dir) );
}
}
Em Java: public int blackHeightRecursive(Node no) {
int altura = 0;
if (!node.isEmpty()) {
if (no.getColour() == Colour.BLACK) {
altura = 1 + Math.max(blackHeightRecursive(no.getLeft()), blackHeightRecursive(no.getRight()));
} else {
altura = Math.max(blackHeightRecursive(no.getLeft()), blackHeightRecursive(no.getRight()));
}
}
return altura;
}
Bibliografia
Ver tambémReferênciasLigações externasDemonstrações
Implementações |
||||||||||||||||||||||||||||||||||