遷移状態理論

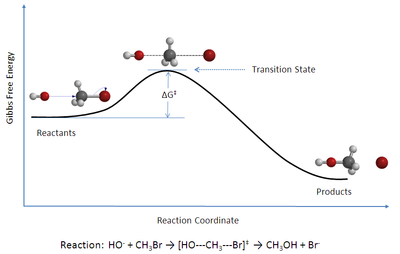
図1: ブロモメタンと水酸化物イオンとの間の2分子的求核置換（S_N2）反応の反応座標図

遷移状態理論（せんいじょうたいりろん、英: Transition state theory、略称: TST）は、素化学反応の反応速度を説明する。本理論は反応物と活性化した遷移状態複合体との間の特別な種類の化学平衡（擬平衡、準平衡）を仮定する[1]。

TSTは、どのように化学反応が起こるかを定性的に理解するために主に使われる。TSTは絶対反応速度定数を計算するというその当初の目標についてはあまり成功していない。これは、絶対反応速度の計算にはポテンシャルエネルギー面の正確な情報が必要なためである[2]。しかし、速度定数が実験的に決定されている特定の反応についての標準活性化エンタルピー（ΔH^‡、Δ^‡H^ɵとも書かれる）、標準活性化エントロピー（英語版）（ΔS^‡またはΔ^‡S^ɵ）、および標準活性化ギブズエネルギー（ΔG^‡またはΔ^‡G^ɵ）の計算には成功している（^‡表記は興味ある値が「遷移状態のもの」であることを指す; ΔH^‡は遷移状態のエンタルピーと反応物のエンタルピーの差である）。

この理論は1935年に（当時プリンストン大学の）ヘンリー・アイリングと（マンチェスター大学の）メレディス・グウィン・エヴァンス（英語版）とマイケル・ポランニーによって同時に構築された[3][4]。TSTは「活性錯合体理論」、「絶対速度理論」、「絶対反応速度理論」とも呼ばれる[5]。

TSTの構築前は、アレニウスの速度則が反応障壁についてのエネルギーを決定するために広く使われた。アレニウスの式は経験的観察から導かれ、1つかそれ以上の反応中間体が反応物（始原系）から生成物（生成系）への変換に関与しているのかといった機構的考察を無視している[6]。したがって、この法則と関連した2つのパラメータ、前指数因子（英語版）（A）と活性化エネルギー（E_a）を理解するためにはさらなる理論の発展が必要であった。アイリングの式をもたらしたTSTはこれら2つの問題の解決に成功した。しかしながら、アレニウスの速度則が発表された1889年から、アイリングの式がTSTから導かれた1935年まで、46年が経過していた。この間、多くの科学者と研究者がこの理論の発展に大きく貢献した。

理論

遷移状態理論の背景にある基本的な考え方は以下の通りである。

1. 反応の速度は、ポテンシャルエネルギー面の鞍点近くの活性複合体（活性錯合体）を調べることによって研究することができる。これらの複合体がどのように形成されるかの詳細は重要ではない。鞍点それ自身が遷移状態と呼ばれる。
2. 活性複合体は反応物分子と特別な平衡（擬平衡）にある。
3. 活性複合体は生成物へと変換でき、この変換の速度を計算するために運動論を使用することができる。

発展

TSTの発展において、以下に要約したように3つのアプローチが取られた。

熱力学的取り扱い

1884年、ヤコブス・ファント・ホッフは、可逆反応についての平衡定数の温度依存性を記述するファントホッフの式を提唱した。

${\displaystyle {\ce {{A}<=> {B}}}}$

${\displaystyle {\frac {d\ln K}{dT}}={\frac {\Delta U}{RT^{2}}}}$

上式において、ΔUは内部エネルギーの変化、kは反応の平衡定数、Rは気体定数、Tは熱力学的温度である。実験結果に基づいて、1889年にスヴァンテ・アレニウスは反応の速度定数について同様の式を提唱した。

${\displaystyle {\frac {d\ln k}{dT}}={\frac {\Delta E}{RT^{2}}}}$

この式を積分するとアレニウスの式

${\displaystyle k=Ae^{-E_{a}/RT}}$

が導かれる（kは速度定数）。Aは頻度因子（現在は前指数因子と呼ばれる）と呼ばれ、E_aは活性化エネルギーと見なされる。20世紀初頭までに、多くの科学者はアレニウスの式を受け入れていたが、AおよびE_aの物理学的解釈はいまだ漠然としていた。そのため、化学反応速度論の多くの研究者が、AとE_aを化学反応に必要な分子運動と直接的に結び付ける試みのなかで、どのように化学反応が起こるかについての様々な理論を提唱した^[要出典]。

1910年、フランスの化学者ルネ・マルセラン（英語版）が標準活性化ギブズエネルギーの概念を導入した。これは

${\displaystyle k\propto \exp \left({\frac {-\Delta ^{\ddagger }G^{\ominus }}{RT}}\right)}$

と書くことができる。

マルスランが彼の理論の構築について研究していたのと同じ頃、オランダの化学者Philip Abraham Kohnstamm、Frans Eppo Cornelis Scheffer、Wiedold Frans Brandsmaが標準活性化エントロピーと標準活性化エンタルピーを導入した。彼らは以下の反応速度式を提唱した。

${\displaystyle k\propto \exp \left({\frac {\Delta ^{\ddagger }S^{\ominus }}{R}}\right)\exp \left({\frac {-\Delta ^{\ddagger }H^{\ominus }}{RT}}\right)}$

しかしながら、この定数の本質は不明なままであった。

運動理論的取り扱い

1900年初頭、マックス・トラウツ（英語版）とウィリアム・ルイス（英語版）は気体分子運動論に基づく衝突理論（英語版）を使って反応速度を研究した。衝突理論は、反応する分子を互いに衝突する剛体球として扱う。この理論は、分子間の衝突が完全に弾性的であると仮定するため、エントロピー変化を無視する。

ルイスは彼の取り扱いを以下の式に適用し、実験値とのよい一致を得た。

2HI → H₂ + I₂

しかしながら、その後に同じ取り扱いが他の反応に適用されると、理論的な結果と実験結果との間には大きな相違があった。

統計力学的取り扱い

統計力学はTSTの構築において大きな役割を果たした。しかしながら、19世紀中頃にジェームズ・クラーク・マクスウェル、ルートヴィッヒ・ボルツマン、レオポルト・プファウントラー（英語版）が分子運動と分子速度の統計学的分布の観点から反応平衡と速度について議論した複数の論文を出版した事実を鑑みると、統計力学のTSTへの応用は非常にゆっくりと進展した。

フランスの化学者A. Berthoudがマクスウェル＝ボルツマン分布を使って反応速度に関する式

${\displaystyle {\frac {d\ln k}{dT}}={\frac {a-bT}{RT^{2}}}}$

（aおよびbはエネルギー項と関連した定数）を得たのは1912年のことだった。

その2年後、ルネ・マルセランは化学反応の進行を位相空間における点の運動として取り扱うことによって本質的な貢献を行った。マルセランは次に、ギブズの統計力学的手順を適用し、以前に熱力学的考察から自身が得ていたものと似た式を得た。

1915年、イギリスの物理学者James Riceが重要な貢献を行った。自身の統計解析に基づき、Riceは反応速度が「critical increment」（臨界増量）に比例すると結論付けた。彼の着想はリチャード・チェイス・トールマンによってさらに発展した。1919年、オーストリアの物理学者カール・フェルディナント・ヘルツフェルト（英語版）は統計力学を平衡定数に、そして運動理論を二原子分子の可逆的解離についての逆反応の速度定数k₋₁に適用した[7]。

${\displaystyle {\ce {AB <=>[k_1][k_{-1}] {A}+ {B}}}}$

ヘルツフェルトは順反応の速度定数に対して以下の式を得た[8]。

${\displaystyle k_{1}={\frac {k_{\mathrm {B} }T}{h}}\left(1-e^{-{\frac {h\nu }{k_{B}T}}}\right)\exp \left({\frac {-E^{\ominus }}{RT}}\right)}$

上式において、${\displaystyle \textstyle E^{\ominus }}$は絶対零度における解離エネルギー、k_Bはボルツマン定数、hはプランク定数、Tは熱力学的温度、${\displaystyle \nu }$は結合の振動周波数である。この式は、TSTの重要な要素である因子k_BT/hが速度方程式に初めて登場したことから、非常に重要である。

1920年、アメリカの化学者リチャード・チェイス・トールマンがRiceのcritical incrementの着想をさらに発展させた。トールマンは、反応のcritical increment（現在は活性化エネルギーと呼ばれる）が反応を起こしている全分子の平均エネルギーから全ての反応物分子の平均エネルギーを引いたものに等しいと結論付けた。

ポテンシャルエネルギー面

ポテンシャルエネルギー面の概念はTSTの発展において非常に重要であった。この概念の基礎は1913年にルネ・マルセランによって築かれた。マルセランは、化学反応の進行が原子の運動量と距離の座標を持つポテンシャルエネルギー面における点として記述できると理論化した。

1931年、ヘンリー・アイリングとマイケル・ポランニーは以下の反応に対するポテンシャルエネルギー面を構築した。この面は、量子力学的諸原理ならびに振動周波数および解離エネルギーの実験データに基づく3次元図である。

H + H₂ → H₂ + H

アイリングとポランニーの構築から1年後、ハンス・ペルツァーとユージン・ウィグナーはポテンシャルエネルギー面上の反応の進行をたどることによって重要な貢献を行った。この成果の重要性は、初めてポテンシャルエネルギー面における鞍点（鞍部（英語版））の概念が議論されたことであった。彼らは反応の速度が鞍部を経る系の運動によって決定される、と結論付けた。

典型的には、律速点（最低鞍点）は初期の基底状態と同じエネルギー面上に位置している、と仮定されてきた。しかしながら、最近、半導体および絶縁体中で起こる過程についてはこれは誤っているかもしれないことが明らかにされた。これらの材料中では、初期励起状態が、初期基底状態の面上の鞍点よりも低い鞍点を通過することができる[9]。

アイリングの式の正当性

アイリング、ポランニー、およびエヴァンスによって導入された最も重要な要素の1つが、活性複合体が反応物と擬平衡状態にある、という考え方であった。その結果、反応速度は、これらの複合体の濃度に複合体が生成物へと変換される周波数（k_BT/h）を乗じたものに正比例する。下部に、アイリングの式の関数形式について厳密でない妥当性の主張（plausibility argument）が示される。しかしながら、鍵となる統計力学的因子k_BT/hは正当化されず、下に示されている論拠はアイリングの式の真の「導出」を構成しない[10]。

擬平衡仮定

擬平衡は古典的な化学平衡とは異なるが、類似した熱力学的取扱いを使って記述することができる[5] [11]。以下の反応について考える。

${\displaystyle {\ce {{A}+{B}<=>{[AB]^{\ddagger }}->{P}}}}$

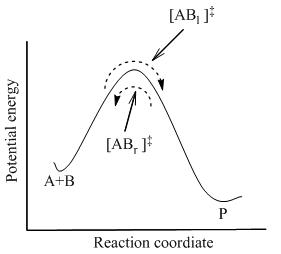
図2: ポテンシャルエネルギー図

ここでは、活性複合体 [AB]^‡ を含む系中の全ての化学種間で完全な平衡が達成される。統計力学を使って、[AB]^‡ の濃度はAとBの濃度の観点から計算することができる。

TSTは、反応物と生成物が互いに平衡状態にない時でさえも、活性複合体が反応物と擬平衡状態にあると仮定する。図2で示されているように、いかなる瞬間においても、少数の活性複合体が存在し、一部は直近の過去には反応物であり、これは [AB_l]^‡と呼ばれる（左から右へ移動するため）。残りは直近の過去には生成物分子であった（[AB_r]^‡）。

TSTでは、活性複合体2方向の流れは互い独立していると仮定される。すなわち、全ての生成物分子が反応系から突然取り除かれたとすると、[AB_r]^‡の流れは止まるが、左から右への流れはまだ存在する。したがって、技術的に正しく言えば、反応物は [AB_l]^‡（直近の過去に反応物だった活性複合体）のみと平衡状態にある。

妥当性の主張

活性複合体はエネルギーのボルツマン分布に従わないが、「平衡定数」は活性複合体が従う分布から導出することができる。この擬平衡ついての平衡定数K^‡は

${\displaystyle K^{\ddagger }={\frac {\ce {[AB]^{\ddagger }}}{\ce {[A][B]}}}}$

と書くことができる。

そのため、遷移状態AB^‡の濃度は

${\displaystyle [{\ce {AB}}]^{\ddagger }=K^{\ddagger }[{\ce {A}}][{\ce {B}}]}$

である。

したがって、生成物が生成する速度式は

${\displaystyle {\frac {d[{\ce {P}}]}{dt}}=k^{\ddagger }[{\ce {AB}}]^{\ddagger }=k^{\ddagger }K^{\ddagger }[{\ce {A}}][{\ce {B}}]=k[{\ce {A}}][{\ce {B}}]}$

となる。上式において、速度定数kは

${\displaystyle k=k^{\ddagger }K^{\ddagger }}$

で与えられる。

ここで、k^‡は活性複合体を生成物へと変化させるのに必要な振動モードの周波数に正比例する; この振動モードの周波数は${\displaystyle \nu }$である。全ての振動が必ずしも生成物の形成をもたらさず、透過係数と呼ばれる比例定数${\displaystyle \kappa }$がこの効果を説明するために導入される。k^‡は

${\displaystyle k^{\ddagger }=\kappa \nu }$

と書くことができる。

平衡定数K^‡について、統計力学は以下の温度依存式をもたらす。

${\displaystyle K^{\ddagger }={\frac {k_{B}T}{h\nu }}K^{\ddagger '}}$ (${\displaystyle K^{\ddagger '}=:e^{\frac {-\Delta G^{\ddagger }}{RT}}}$)

k^‡とK^‡についての新しい式を組み合わせると、新しい速度定数式を

${\displaystyle k=k^{\ddagger }K^{\ddagger }=\kappa {\frac {k_{B}T}{h}}e^{\frac {-\Delta G^{\ddagger }}{RT}}=\kappa {\frac {k_{B}T}{h}}K^{\ddagger '}}$

と書くことができる。

定義により、ΔG^‡ = ΔH^‡ –TΔS^‡であるため、この速度定数式は以下のように展開でき、アイリングの式の別形式が与えられる。

${\displaystyle k=\kappa {\frac {k_{B}T}{h}}e^{\frac {\Delta S^{\ddagger }}{R}}e^{\frac {-\Delta H^{\ddagger }}{RT}}}$.

正しい次元性のため、この式は単分子的ではない反応のための追加因子 (c^⊖)^1–mを持つ必要がある。

${\displaystyle k=\kappa {\frac {k_{B}T}{h}}e^{\frac {\Delta S^{\ddagger }}{R}}e^{\frac {-\Delta H^{\ddagger }}{RT}}(c^{\ominus })^{1-m}}$

上式において、c^⊖は標準濃度1 mol L^–1、mは分子度である[12]。

遷移状態理論からの推論とアレニウスの理論との関係

遷移状態理論から得られた速度定数式は、実験的な反応速度データを使ってΔG^‡、ΔH^‡、ΔS^‡、そしてΔV^‡（活性化の体積）さえも計算するために使うことができる。これらのいわゆる「活性化パラメータ」は、エネルギー容量と秩序度など出発物質と比較した遷移状態の特性について洞察を与え、物理有機化学において反応機構を解明するための標準的ツールとなった。活性化自由エネルギーΔG^‡は遷移状態理論において${\displaystyle \Delta G^{\ddagger }=-RT\ln K^{\ddagger '}}$を満たすようなエネルギーとして「定義」される。パラメータΔH^‡およびΔS^‡は次に異なる温度でΔG^‡ = ΔH^‡ – TΔS^‡を決定することによって推定される。

アイリングの式とアレニウスの式の関数形式は似ているため、活性化パラメータをアレニウスの表現方法の活性化エネルギーおよび前指数因子とつい関連付けたくなる。しかしながら、アレニウスの式は実験データから導かれたものであり、反応機構における遷移状態の数に関係なく、2つのパラメータのみを使って巨視的速度をモデル化する。対照的に、活性化パラメータは、少なくとも原理的には、多段階機構の全ての遷移状態について見出すことができる。したがって、活性化エンタルピーΔH^‡はしばしばアレニウスの活性化エネルギーE_aと同一視されるものの、これらは等価ではない。凝縮相（例えば溶液相）または単分子的気相反応段階について、E_a = ΔH^‡ + RTである。他の気相反応では、E_a = ΔH^‡ + (1 − Δn^‡)RTである。（Δn^‡は遷移状態を形成する際の分子数の変化）[13]。したがって、二分子気相過程では、E_a = ΔH^‡ + 2RTとなる。

活性化エントロピーΔS^‡は、（反応に関与するあるいは反応によって摂動を受ける溶媒分子を含む）遷移状態が出発物質を比較してより無秩序である程度を与える。これは、アレニウスの式の前指数因子Aの具体的な解釈を与える; 単分子的、一段階過程では、大まかな等価性A = (k_BT/h) exp(1 + ΔS^‡/R) が成り立つ（二分子的気相反応では A = (k_BT/h) exp(2 + ΔS^‡/R)）。単分子過程では、負の値は基底状態よりも秩序だった、硬い遷移状態を示すのに対して、正の値は遷移状態がより緩い結合とより大きな配座的自由度の両方またはいずれか一方を持っていることを反映している。次元性の理由のため、二分子的またはそれ以上の反応は選択した標準状態（具体的に言うと、標準濃度）に依存したΔS^‡値を持つことに注意することが重要である。近年のほとんどの文献において、1 mol L^–1（1モーラー）が選ばれる。この選択はモル量と体積についての単位の我々の定義に基づく人間による産物であるため、単一の反応についてのΔS^‡の大きさと符号はそれ自体では無意味である。同じ標準状態で決定された「既知の」（または想定される）機構の参照反応の値との比較のみが妥当である[14]。

活性化体積は、（温度一定での）圧力に関するΔG^‡の偏微分を議論することによって見出される。

${\displaystyle \Delta V^{\ddagger }:=(\partial \Delta G^{\ddagger }/\partial P)_{T}}$

これは、遷移状態の大きさ、したがって結合の度合いに関する情報を与える。結合的機構は負の活性化体積をおそらく持つのに対して、解離的機構は正の値をおそらく持つ。

平衡定数と順および逆速度定数との間の関係${\displaystyle K=k_{1}/k_{-1}}$を考えると、アイリングの式は

${\displaystyle \Delta G^{\circ }=\Delta G_{1}^{\ddagger }-\Delta G_{-1}^{\ddagger }}$

ということになる。

TSTのもう1つの暗示はカーティン–ハメットの原理（英語版）である: Rから2つの生成物AおよびBが得られる速度論的に支配（制御）された反応（英語版）の生成物比は生成物をもたらす各遷移状態のエネルギー差を反映する（それぞれの生成物に単一の遷移状態を仮定する）。

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=e^{-\Delta \Delta G^{\ddagger }/RT}}$

(${\displaystyle \Delta \Delta G^{\ddagger }=\Delta G_{\mathrm {A} }^{\ddagger }-\Delta G_{\mathrm {B} }^{\ddagger }}$)

（上記のΔΔG^‡についての式では、もしAおよびBが平衡状態にある2つの異なる化学種S_AおよびS_Bから形成されるならば追加の${\displaystyle \Delta G^{\circ }=G_{\mathrm {S} _{\mathrm {A} }}^{\circ }-G_{\mathrm {S} _{\mathrm {B} }}^{\circ }}$項が存在する。）

1.36ルール

熱力学的に支配された反応では、生成物AとBの自由エネルギーにおいてRT ln 10 ≈ (1.987 × 10^–3 kcal/mol K)(298 K)(2.303) ≈ 1.36 kcal/molの差毎に室温（298 K）での選択性が10倍になる。

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=10^{-\Delta G^{\circ }/(1.36\ \mathrm {kcal/mol} )}}$

(${\displaystyle \Delta G^{\circ }=G_{\mathrm {A} }^{\circ }-G_{\mathrm {B} }^{\circ }}$)

類似的に、活性化自由エントロピーの差1.36 kcal/mol毎に室温での速度論支配過程についての選択性（英語版）は10倍になる[15]。

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=10^{-\Delta \Delta G^{\ddagger }/(1.36\ \mathrm {kcal/mol} )}}$

(${\displaystyle \Delta \Delta G^{\ddagger }=\Delta G_{\mathrm {A} }^{\ddagger }-\Delta G_{\mathrm {B} }^{\ddagger }}$).

概算

アイリングの式を使うと、特定の温度でのΔG^‡、一次速度定数、および反応半減期の間に直接的な関係が存在する。298 Kでは、ΔG^‡ = 23 kcal/molの反応はk ≈ 8.4 × 10^–5 s^–1の速度定数とt_1/2 ≈ 2.3時間の半減期を持つ。これらの数字はしばしばk ~ 10^–4 s^–1とt_1/2 ~ 2 hに丸められる。したがって、この大きさの活性化自由エネルギーは室温、一晩で終了まで進行する典型的な反応に対応する。比較のため、シクロヘキサンのいす反転（英語版）はおよそ11 kcal/molのΔG^‡とk ~ 10^5 s^–1の速度定数を有する。したがって、これは室温で（NMR時間スケールよりも速く）迅速に起こる動的過程となる。反対側では、2-ブテンのシス/トランス異性化はおよそ60 kcal/molのΔG^‡を持ち、298 Kでk ~ 10^–31 s^–1に相当する。これは無視できる速度である。半減期は12桁で、宇宙の年齢よりも長い[16]。

限界

一般に、TSTは研究者らに化学反応がどのように起こるかを理解するための概念的基盤を与えてきた。たとえ本理論が広く適用できるとしても、限界がある。例えば、多段階反応の個々の素過程に適用する時、本理論は個々の中間体が次の段階に進む前にエネルギーのボルツマン分布に達するのに十分長寿命であること仮定する。中間体が非常に短寿命である時、TSTは破綻する。こういった場合、反応物から中間体への反応軌跡の運動量が生成物の選択性に影響を及ぼす可能性がある（こういった反応の一例が、Anslynとドウアティ（英語版）の教科書で示されているジアゾビシクロペンタン類の熱分解である）。

遷移状態理論は、原子核が古典力学に従って振る舞うという仮定にも基づく[17]。原子あるいは分子が遷移構造を形成するために十分なエネルギーを持って衝突しない限り、反応は起こらない、と仮定される。しかしながら、量子力学によれば、有限の量のエネルギーを持ついかなる障壁についても、粒子が障壁の向こう側へトンネリングできる可能性が存在する（トンネル効果）。化学反応に関してこれは、分子がエネルギー障壁を越えるのに十分なエネルギーを持って衝突しないとしても反応する可能性が存在することを意味する[18]。この効果は大きな活性化エネルギーを持つ反応については無視できるが、トンネリング確率は障壁の高さが低くなるほど大きくなるため、比較的低エネルギー障壁を持つ反応については重要な現象となる。

遷移状態理論は高温での一部の反応について破綻する。本理論は、反応系がポテンシャルエネルギー面の最低エネルギー鞍点を通過することを仮定する。この描写は比較的低温で起こる反応についてはつじつまが合っているが、高温では分子はより高いエネルギー振動モードを占有する。それらの運動はより複雑となり、衝突の結果として最低エネルギー鞍点から遠く離れた遷移状態がもたらされるかもしれない。遷移状態理論からのこのずれは二原子水素と水素ラジカルとの間の単純な交換反応においてさえも観測される[19]。

これらの限界を考慮して、複数の遷移状態理論の代替理論が提唱されてきた。これらの理論についての簡潔な解説を以下に示す。

一般化遷移状態理論

小正準（ミクロカノニカル）変分型TST、正準（カノニカル）変分型TST（英語版）、および改良正準変分型TSTといった遷移状態が必ずしも鞍点に位置していないTSTは、一般化遷移状態理論と呼ばれる。

小正準変分型TST

遷移状態理論の根本的な欠陥は、反応物から生成物またはその逆の反応として遷移状態の全ての交差を数えることである。現実には、分子はこの「分割面」を越えて引き換えすかもしれず、あるいは複数回越えて、本当に一度しか反応しないかもしれない。そのため、未補正のTSTは速度係数の上界しか与えない、と言われる。これを補正するため、変分型遷移状態理論はそれぞれの固定エネルギーについて反応速度を最小化するためにうまくいく反応を定義する分割面の位置を変動させる[20]。この小正準的取り扱いで得られた速度式はエネルギーにわたって積分することができる。これは、正準（熱的）速度を与えるために、エネルギー状態にわたる統計学的分布を考慮に入れている。

正準変分型TST

特定の温度における速度定数を最小化するために分割面の位置を変動させる遷移状態理論の発展。

改良正準変分型TST

正準変分型遷移状態理論の修正。閾値エネルギーより下のエネルギーにつしては、分割面の位置は小正準閾値エネルギーのものとされる。これにより、閾値エネルギー未満ならば、速度定数への寄与はゼロになる。次に、より高いエネルギーを持つ反応物によって成される速度定数への寄与を最小化するように妥協分割面が選択される。

非断熱TST

2つのスピン状態が同時に関与する反応へのTSTの拡張は非断熱遷移状態理論（英語版）（NA-TST）と呼ばれる。

半古典的TST

振動摂動理論を使って、トンネリングや変分効果といった効果を半古典的遷移状態理論（英語版）（SCTST）形式内で説明することができる。

脚注

1. IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). オンライン版:  (2006-) "transition state theory".
2. Truhlar, D. G.; Garrett, B. C.; Klippenstein, S. J. (1996). “Current Status of Transition-State Theory”. J. Phys. Chem. 100 (31): 12771–12800. doi:10.1021/jp953748q. 
3. Laidler, K.; King, C. (1983). “Development of transition-state theory”. J. Phys. Chem. 87 (15): 2657. doi:10.1021/j100238a002. 
4. Laidler, K.; King, C. (1998). “A lifetime of transition-state theory”. The Chemical Intelligencer 4 (3): 39. 
5. ^ Laidler, K. J. (1969). Theories of Chemical Reaction Rates. McGraw-Hill 
6. Anslyn, E. V.; Dougherty, D. A. (2006). “Transition State Theory and Related Topics”. Modern Physical Organic Chemistry. University Science Books. pp. 365–373. ISBN 1891389319 
7. Herzfeld, K. E. (1919). “Zur Theorie der Reaktionsgeschwindigkeiten in Gasen”. Annalen der Physik 364 (15): 635–667. Bibcode: 1919AnP...364..635H. doi:10.1002/andp.19193641504. https://zenodo.org/record/1424347. 
8. Keith J. Laidler, Chemical Kinetics (3rd ed., Harper & Row 1987), p.88 ISBN 0-06-043862-2
9. Luo, G.; Kuech, T. F.; Morgan, D. (2018). “Transition state redox during dynamical processes in semiconductors and insulators”. NPG Asia Materials 10 (4): 45–51. arXiv:1712.01686. Bibcode: 2018npjAM..10...45L. doi:10.1038/s41427-018-0010-0. 
10. 統計力学の入門的取扱いとアイリングの式の初歩的導出については以下の文献を見よ: Lowry and Richardson, Mechanism and Theory in Organic Chemistry, 3rd ed. (Harper & Row, 1987), pp. 248-253.
11. Steinfeld, Jeffrey L.; Francisco, Joseph S.; Hase, William L. (1999). Chemical Kinetics and Dynamics (2nd ed.). Prentice-Hall. pp. 289-293. ISBN 0-13-737123-3 
12. Laidler, Keith J. (1981). “Symbolism and terminology in chemical kinetics”. Pure and Applied Chemistry (IUPAC) 53: 753-771. http://publications.iupac.org/pac/pdf/1981/pdf/5303x0753.pdf 9 August 2019閲覧. "See p.765, note m." 
13. Steinfeld, Jeffrey L.; Francisco, Joseph S.; Hase, William L. (1999). Chemical Kinetics and Dynamics (2nd ed.). Prentice-Hall. p. 302. ISBN 0-13-737123-3 
14. Carpenter, Barry K. (1984). Determination of organic reaction mechanisms. New York: Wiley. ISBN 0471893692. OCLC 9894996 
15. Lowry, Thomas H. (1987). Mechanism and theory in organic chemistry. Richardson, Kathleen Schueller. (3rd ed.). New York: Harper & Row. ISBN 0060440848. OCLC 14214254. https://archive.org/details/mechanismtheoryi000321 
16. Eliel, Ernest L. (Ernest Ludwig) (1994). Stereochemistry of organic compounds. Wilen, Samuel H., Mander, Lewis N.. New York: Wiley. ISBN 0471016705. OCLC 27642721 
17. Eyring, H. (1935). “The Activated Complex in Chemical Reactions”. J. Chem. Phys. 3 (2): 107–115. Bibcode: 1935JChPh...3..107E. doi:10.1063/1.1749604. 
18. Masel, R. (1996). Principles of Adsorption and Reactions on Solid Surfaces. New York: Wiley 
19. Pineda, J. R.; Schwartz, S. D. (2006). “Protein dynamics and catalysis: The problems of transition state theory and the subtlety of dynamic control”. Phil. Trans. R. Soc. B 361 (1472): 1433–1438. doi:10.1098/rstb.2006.1877. PMC 1647311. PMID 16873129. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1647311/. 
20. Truhlar, D.; Garrett, B. (1984). “Variational Transition State Theory”. Annu. Rev. Phys. Chem. 35: 159–189. Bibcode: 1984ARPC...35..159T. doi:10.1146/annurev.pc.35.100184.001111. https://digital.library.unt.edu/ark:/67531/metadc1209228/. 

参考文献

• Anslyn, Eric V.; Doughtery, Dennis A., Transition State Theory and Related Topics. In Modern Physical Organic Chemistry University Science Books: 2006; pp 365–373
• Cleland, W.W., Isotope Effects: Determination of Enzyme Transition State Structure. Methods in Enzymology 1995, 249, 341-373
• Laidler, K.; King, C., Development of transition-state theory. The Journal of Physical Chemistry 1983, 87, (15), 2657
• Laidler, K., A lifetime of transition-state theory. The Chemical Intelligencer 1998, 4, (3), 39
• Radzicka, A.; Woldenden, R., Transition State and Multisubstrate$Analog Inhibitors. Methods in Enzymology 1995, 249, 284-312
• Schramm, VL., Enzymatic Transition States and Transition State Analog Design. Annual Review of Biochemistry 1998, 67, 693-720
• Schramm, V.L., Enzymatic Transition State Theory and Transition State Analogue Design. Journal of Biological Chemistry 2007, 282, (39), 28297-28300

関連項目

• RRKM理論

外部リンク

• Simple application of TST