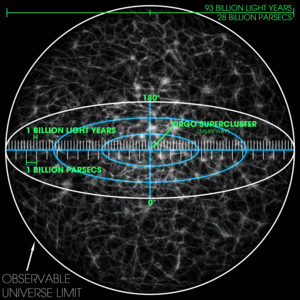
観測可能な宇宙

観測可能な宇宙

観測可能な宇宙の可視化。 このスケールは、細かい粒子が多数の超銀河団の集合を表すようなものである。天の川銀河の存在するおとめ座超銀河団は中心にマークされているが、小さすぎて見えない。
直径	8.8×10^26 m or 880 Ym (28.5 Gパーセク or 930億光年)[1]
体積	3.566×10^80 m^3[2]
重さ	1.5×10^53 kg[注釈 1]
密度	9.9×10^−27 kg/m^3 (1立方m内に6個の陽子が存在するのに等しい)[3]
年齢	137.87±0.20 億年[4]
平均温度	2.72548±0.00057 K[5]
中身	物質 (4.9%) ダークマター (26.8%) ダークエネルギー (68.3%)[6]

近赤外の全天概観により、銀河系（天の川銀河）から遠く離れた銀河の分布が分かる。この画像は、150万以上の銀河を掲載している2MASS Extended Source Catalog (XSC) と、銀河系内の5億の星を掲載しているPoint Source Catalog (PSC) から作成したもの。銀河にはUGC、CfA、Tully NBGC、LCRS、2dF、6dFGS、SDSSの調査（やNASA銀河系外データベース収集のさまざまな観察）で得られた、あるいはKバンド (2.2 µm) より推定された「赤方偏移」によって、色付けがなされている。青色は最も近い光源 (z < 0.01) であり、緑色は中間距離の光源 (0.01 < z < 0.04)、赤色は2MASSの分析中最も遠くの光源 (0.04 < z < 0.1) である。この分布図は銀河系を中心に据え、エイトフ正積図法により投影したものである[7]（Thomas Jarretによる図：IPAC）。

ビッグバン宇宙論でいう観測可能な宇宙（かんそくかのうなうちゅう、observable universe）とは、中心にいる観測者が領域内の物体を十分に観測できるほど小さい、つまり、ビッグバン以後のどの時点でその物体から放出された信号であっても、それが光速で進んで、現在の観測者のもとに届くまでに十分な時間があるような球状の空間領域である。宇宙のどの場所にもその場所にとっての観測可能な宇宙があり、それは地球を中心とするものと重なる部分も重ならない部分もある。

概説

「観測可能」ということは、現代の技術でこの領域内の物体から放射されたエネルギーが検出できるかどうかとは無関係であり、その物体からの光やその他の放射エネルギーが地球上の観測者のもとに到達することが原理上可能だという意味である。実際に観察できるのは、宇宙が晴れ上がった「最終散乱面」にある物体までである。晴れ上がる前の宇宙は、光子に対して不透明であった。しかしながら、重力波（やはり光速で移動している）の検出によって、それ以前の情報を推定することもできないわけではない。重力波はインフレーション時代の遅くとも後期から発生しており、それによって数兆光年・あるいはそれ以上の遠方の宇宙を観測できる可能性がある（もちろんインフレーション時代の宇宙の姿の観測となる）。

観測可能な宇宙と全宇宙

観測可能な宇宙を対数スケールで表した図。太陽系を中心としており、各天体には名称を付けている。太陽からの各天体の距離は、中心から端に向かって指数関数的に増加している。また、天体の形状が分かるように各天体を拡大している。

科学者から観測された事実として頻繁に発表・公表される宇宙の具体的な観測値は、あくまで観測可能な宇宙に関するものに限られている。

だが現代宇宙論の構築、宇宙のインフレーションなどの信頼できる多くの理論の説明では、観測可能な宇宙の外側に広がる広大な宇宙を含む、より巨大な全宇宙に関する考察が必要になる。

全宇宙が観測可能な宇宙よりも「小さい」ということも、もちろん可能である。その場合、非常に遠くにあるように見える銀河が、実は近くにある銀河の光が宇宙を一周してくることによって生じた複製像だということもあり得る。この仮説を実験によってテストするのは、銀河の異なる像がその一生の異なる時代を指すこともあり、結果としてまったく違うということにもなりかねないため、困難である。2004年のある論文[8]では、全宇宙の直径は、24ギガパーセク（780億光年）が下限であると主張されており、その場合、観測可能な宇宙より少しだけ小さいということになる。この値はWMAPの観測をマッチング・サークル分析したものに基づいている。

仮に観測不可能な宇宙を含めた全宇宙が有限で閉じているとしても、観測可能な宇宙の範囲内では、曲率は無視できるほど小さいことから、宇宙全体の大きさは、光年単位を用いても「兆」などの日常的な数の尺度、あるいは命数法レベルの数の尺度ではなく、指数での表現が必要な大きさ、それもA×10^Bといった単純な仮数指数表記ではなく、指数の上に指数を重ねた指数タワーでの表現が必要な大きさである。レオナルド・サスキンドは宇宙の直径を${\displaystyle 10^{10^{10^{122}}}}$と推定している。この推定値はグーゴルプレックスプレックスより大きいが、この見積もりにおいて単位は一切考慮されていない。桁数が非常に大きいため、単位が「ヨタパーセク」でも「光年」でも「メートル」でも「プランク長」でも、もはや誤差以下の違いでしかないためである（巨大数の項目も参照）。具体的に説明すると、単位付与は値に対して定数倍の効果を持つが、1ヨタパーセクは1プランク長の1.9×10^75倍であり、${\displaystyle 10^{10^{10^{122}}}}$の値のオーダーの前には桁数が少なすぎて、議論の本質に影響を及ぼすことがないということである。

さまざまな予測は提唱されているものの、全宇宙の大きさがどれくらいなのかは2023年現在の観測技術を以てしても推定すら不可能であり、まったくの未解明となっている。これは全宇宙がどれほど巨大であろうが現代宇宙論と矛盾しないためである。インフレーション理論においては無限に近いスケールの膨張も許容されていて、理論上は大きさの上限がない。観測可能な宇宙の範囲内の曲率が測定限界を下回って限りなく0に近いことや、磁気単極子が発見されていないことなどの観測事実から、最低でも観測可能な宇宙より数十桁以上大きいと見られる程度である。全宇宙の広さは「ほぼ無限」と説明されることも多いが、これは決して大袈裟な表現ではない。なお、「ビッグバン直後の宇宙はバスケットボール程度の大きさだった」などの例え話は通常、観測可能な宇宙のみを指して使われる表現だが、誤解を招き易いので注意が必要である。

宇宙の大きさ

地球から「可視」宇宙（宇宙光の地平面）の端までの共動距離は、あらゆる方向に約14ギガパーセク（465億光年）である[9]。これによって、観測可能な宇宙の共動半径の下限が明確になる。もっとも、導入部で述べたように、可視宇宙は観測可能な宇宙よりやや小さいと考えられる。これは、再結合（宇宙の晴れ上がり）以後に放射された宇宙背景放射からの光しか見えないためである。この宇宙背景放射によって、われわれには天体の「最終散乱面」が見えているということになる（重力波によって、あくまで理論上は、この球体の外部領域から、再結合期以前の事象が観察できる）。つまり、可視宇宙は直径約28ギガパーセク（約930億光年）の球体だということになる。宇宙空間はだいたいユークリッド平面であるから、この大きさはおよそ

${\displaystyle {\frac {4}{3}}\times \pi \times \mathrm {R} ^{3}=4\times 10^{32}{\text{ ly}}^{3}}$

すなわち3×10^80立方メートルの共動体積に相当する。

上に引用した数字は、（宇宙時間でいう）「今」の距離であり、「光が放射された時点における」距離ではない。例えば、今この瞬間にみえる宇宙マイクロ波背景放射 (CMBR) は、137億年前に起こったビッグバンから379,000[10]年後の再結合の時に放射されたものである。この放射エネルギーは、その中間の時期に密集し、現在では銀河になっている物質から放出されたものである。これらの銀河は現在、われわれからおよそ460億光年の距離にあるとされている。光が放出された時点におけるその物質までの距離を推定するためには、「膨張の数学モデル」を選び、また、スケール因子a(t) をビッグバンからの任意の時刻t について計算しなければならない。観察に適したΛ-CDMモデルでは、WMAP衛星からのデータを用い、このような計算によって、およそ1292というスケール因子の変化が得られる。これが意味するのは、宇宙が、CMBR光子が放出されたときの大きさの1292倍に膨張しているということである。よって、現在観測できる最も遠くの物質（460億光年先）は、現在受け取っているマイクロ波が放出されたときには、いずれ地球となる物質からわずか3600「万」光年しか離れていなかったのである。つまり宇宙の膨張により137億光年より遠方の宇宙も「観測可能な宇宙」に含まれたことになり、重力波が最初に発生したインフレーション時期（雑誌ニュートン2012年7月号掲載）にはインフレーションによる急激な膨張により、重力波を発生した物理体が現在では非常に遠方に存在していることになる。

誤解

多くの二次資料がこれまでにさまざまな誤った可視宇宙の大きさを「報告」している。いくつかを例示する。

137億光年

宇宙の年齢は約137億歳である。光より速く進むものはないということが広く知られているので、観測可能な宇宙の半径は137億光年しかないはずだ、という考え方に基づいた値である。この論理は、宇宙が特殊相対論での平らな時空である場合に限って意味をなすものである。しかし実際の宇宙は宇宙スケール上でかなり歪んだ時空連続体であり、三次元空間（だいたい平ら）はハッブルの法則で表されるように膨張しているので、この論理は正確ではない。また、この論理で得られる光速と宇宙時間の積は、いかなる物理的意義をも持たない[11]。

138億光年

非常に単純化されたハッブルの法則から求められる、光速度${\displaystyle c}$をハッブル定数${\displaystyle H_{0}}$で割った値であり、ハッブル距離とも言われる。ハッブル定数が時空に関して普遍であるという前程をおいているため、実際の観測可能な宇宙の距離とは大きく異なる。2000年前後に、新学力観に基づく問題として非常に単純化されたハッブルの法則を用いた問題が難関大学の入学試験で散見され(ハッブルの法則は当時の高校物理の教科書には載っていなかったため、未知の問題への解決力を試す問題としてはよく適していた)、回答としてこの値が広がった。なお、ハッブル時間そのものに物理的意味はない。

158億光年

この数字も137億光年と同じように得られるが、こちらは有名な一般雑誌が2006年中ごろに、宇宙の年齢を誤って公表したことに端を発している[12][13][14]。この主張の分析や、ベースとなっている論文は[15]を参照のこと。

274億光年

これは半径137億光年という誤解にもとづく、直径である。

780億光年

これは、宇宙マイクロ波背景放射(CMBR)の対蹠点間の現在の測定値を基にした、全宇宙の大きさの下限である。そのため、CMBRが形成する球体の「直径」を表している。もし全宇宙がこの球体よりも小さいなら、光はビッグバン以降、球体内を周回するだけの時間があるわけで、CMBRには互いに異なる複数の像を生じ、何重もの円を描くことになる[16]。Cornishらは24ギガパーセク（780億光年）までのスケール値でそのような効果を探したが、結局見つからず、もし自分たちの調査が可能な限り全方位に拡張できるのであれば、「われわれの住む宇宙が直径24ギガパーセクより小さいという可能性を排除できる」はずだと示唆している。さらに、「ノイズが少なく、解像度の高いCMB分布図（WMAPの延長ミッションやプランクからのデータ）」があれば、「より小さい円パターンを探し、下限を28ギガパーセクまで拡張できるであろう」[8]とも推定している。いずれ計画実験で見られるであろうCMBR球体の最大直径は、推定最小値が28ギガパーセクだということになり、半径14ギガパーセクに対応する。これは前節で挙げた数字と一致する。

1560億光年

これは780億光年を半径として、2倍すると得られる。780億光年自体が直径なのだから、2倍すれば誤りである。しかし、あちこちに散見される[17][18][19]。

内容物質

観測可能な宇宙には3×10^22〜7×10^22個（300垓〜700垓個）の星[20]があって800億以上の銀河にまとまり、それぞれがさらに銀河群や銀河団、超銀河団を形成している[21]。

2つの大まかな計算がそれぞれ、観測可能宇宙内の亜原子粒子を約10^80としている。

1. WMAPからのCMBデータを観察すると、宇宙の空間曲率はほぼゼロに近いことが示唆され、これによって、現在の宇宙モデルでは、宇宙の密度パラメータの値が何らかの臨界値に非常に近いことが含意される。総密度は9.9×10^−27 kg/m^3[22]となり、1立方メートルあたり水素原子およそ5.9個分である。WMAPデータの分析結果から、臨界密度の約4.6%が通常の原子形態であり、23%は冷たい暗黒物質 (SDM)、72%はダークエネルギーから成ると考えられている[22]。すると、1立方メートルあたり0.27の水素原子が残り、これに可視宇宙の体積をかければ約8×10^79の水素原子を得る。
2. 典型的な星の質量は2×10^30kgであり、星1つに対して約1×10^57の水素原子があることになる。典型的な銀河には約4000億の星があるから、銀河1つあたり1×10^57 × 4×10^11 = 4×10^68の水素原子がある計算となる。宇宙には800億の銀河があるといわれているので、観測可能な宇宙には4×10^68 × 8×10^10 = 3×10^79の水素原子がある。しかしこれは下限を示したに過ぎず、また水素原子は星以外にも存在する[23]。

観測可能な宇宙の質量

観測可能な宇宙内の物質質量は密度と大きさから推定可能である[24]。

星の密度の測定値に基づいた推定

観測可能な宇宙を構成する可視物質の質量を計算する方法は、1つには、平均太陽質量を仮定し、これに観測可能宇宙内の星の総数をかけることである。宇宙の星の推定総数は、観測可能な宇宙の体積

${\displaystyle {\frac {4}{3}}\pi {S_{\textrm {horizon}}}^{3}=9\times 10^{30}\ {\textrm {ly}}^{3}}$

と、ハッブル宇宙望遠鏡の観測値から計算した星の密度

${\displaystyle {\frac {5\times 10^{21}\ {\textrm {stars}}}{4\times 10^{30}\ {\textrm {light-years}}^{3}}}=10^{-9}\ {\textrm {stars}}/{\textrm {ly}}^{3}}$

から導かれ、観測可能な宇宙内の星の推定総数は9×10^21（90垓）個となる。

太陽の質量（2×10^30 kg）を平均太陽質量（矮星の多さと、太陽より質量の大きな星の数はつりあっているとする）とし、星の総数を10^22個とすれば、観測可能な宇宙の星の総質量は3×10^52 kgとなる[25]。しかしながら、「内容物質」の節で述べたように、WMAPのデータはΛ-CDMモデルで推定すると、観測可能な宇宙の総質量の5%未満が星などの可視的な物質で構成されており、残りは暗黒物質やダーク・エネルギーが占めていると予測される。

フレッド・ホイルは観測可能な定常宇宙の質量を、

${\displaystyle {\frac {4}{3}}\cdot \pi \cdot \rho \cdot \left({\frac {c}{H}}\right)^{3}}$

という式を用いて計算している。この式は、

${\displaystyle {\frac {c^{3}}{2GH}}.}$[26]

と書くこともできる。

脚注

注釈

1. Multiply percentage of ordinary matter given by Planck below, with total energy density given by WMAP below

出典

1. Itzhak Bars; John Terning (2009). Extra Dimensions in Space and Time. Springer. pp. 27–. ISBN 978-0387776378. https://books.google.com/books?id=fFSMatekilIC&pg=PA27 2011年5月1日閲覧。 
2. “volume universe Wolfram|Alpha”. www.wolframalpha.com. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
3. “What is the Universe Made Of?”. NASA. June 1, 2022閲覧。
4. Planck Collaboration (2020). “Planck 2018 results. VI. Cosmological parameters”. Astronomy & Astrophysics 641: page A6 (see PDF page 15, Table 2: "Age/Gyr", last column). arXiv:1807.06209. Bibcode: 2020A&A...641A...6P. doi:10.1051/0004-6361/201833910. 
5. Fixsen, D. J. (December 2009). “The Temperature of the Cosmic Microwave Background”. The Astrophysical Journal 707 (2): 916–920. arXiv:0911.1955. Bibcode: 2009ApJ...707..916F. doi:10.1088/0004-637X/707/2/916. 
6. “Planck cosmic recipe”. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
7. "Large Scale Structure in the Local Universe: The 2MASS Galaxy Catalog", Jarrett, T.H. 2004, PASA, 21, 396
8. ^ Neil J. Cornish, David N. Spergel, Glenn D. Starkman, and Eiichiro Komatsu, Constraining the Topology of the Universe. Phys. Rev. Lett. 92, 201302 (2004). astro-ph/0310233
9. Lineweaver, Charles; Tamara M. Davis (2005年). “Misconceptions about the Big Bang”. Scientific American. 2008年11月6日閲覧。
10. Abbott, Brian (May 30, 2007). “Microwave (WMAP) All-Sky Survey”. Hayden Planetarium. 2008年1月13日閲覧。
11. Ned Wright, "Why the Light Travel Time Distance should not be used in Press Releases".
12. SPACE.com - Universe Might be Bigger and Older than Expected
13. Big bang pushed back two billion years - space - 04 August 2006 - New Scientist Space
14. 2 billion years added to age of universe
15. Edward L. Wright, "An Older but Larger Universe?".
16. Bob Gardner's "Topology, Cosmology and Shape of Space" Talk, Section 7
17. SPACE.com - Universe Measured: We're 156 Billion Light-years Wide!
18. New study super-sizes the universe - Space.com - MSNBC.com
19. BBC NEWS | Science/Nature | Astronomers size up the Universe
20. “Astronomers count the stars”. BBC News. (July 22, 2003). http://news.bbc.co.uk/2/hi/science/nature/3085885.stm 2006年7月18日閲覧。 
21. How many galaxies in the Universe? は、「ハッブル宇宙望遠鏡は800億の銀河を検出可能である。実際は、観測可能な宇宙内でも、これよりさらに多いに違いない。われわれのすぐ隣にある最もよく知られた銀河でさえ小さくおぼろげにしか見えず、はっきりと見ることは困難を極めるのに、宇宙距離の離れた銀河はなおさらのことである」としている。
22. ^ WMAP- Content of the Universe
23. Matthew Champion, "Re: How many atoms make up the universe?", 1998
24. McPherson, Kristine (2006年). “Mass of the Universe”. The Physics Factbook. March 23, 2008閲覧。
25. (PDF) On the expansion of the universe. NASA Glenn Research Centre. http://www.grc.nasa.gov/WWW/K-12/Numbers/Math/documents/ON_the_EXPANSION_of_the_UNIVERSE.pdf. 
26. Helge Kragh (1999-02-22). Cosmology and Controversy: The Historical Development of Two Theories of the Universe. Princeton University Press. pp. 212. ISBN 0-691-00546-X