|
ベーテの式ベーテの式(英: Bethe formula)とは、高速の荷電粒子(陽子、アルファ粒子、イオン)が物質を通過するとき移動距離あたりに失うエネルギーの平均量を表す式である(この量は阻止能と呼ばれる)[1]。名はハンス・ベーテにちなむ。ベーテは1930年に非相対論的な表式を導き、1932年には相対論的な表式(後述)を作り出した[2]。ベーテ・ブロッホの式(英: Bethe-Bloch equation)と呼ばれることもある。 物質内を移動する高速の荷電粒子は、物質中の原子が持つ電子と相互作用を行ってその原子を励起もしくは電離させ、それと引き換えにエネルギーを失う。エネルギー損失の最確値は平均値とは一致せず、ランダウ-バビロフ分布に従う[3]。飛んでいる粒子が電子である場合、質量が小さいため相対論補正が必要となり、また衝突相手の電子と区別できなくなる性質があるため失われるエネルギー量はわずかに異なる。さらに制動放射による損失も大きいのでその項を追加する必要がある。 式電子密度 n のターゲット物質に電気素量 e の z 倍の電荷を持つ粒子が入射する場合を考える。物質内の移動距離を x 、粒子の速度を v 、エネルギーを E として、相対論効果を含めたベーテの式は国際単位系で以下のように表される[2]。 (1) ここで c は光速度、ε0 は真空の誘電率、me は電子の静止質量を意味する。また β = v/c である。I は平均励起ポテンシャルと呼ばれる量で、ターゲット物質の原子が荷電粒子から受ける励起の平均的なエネルギーを表す。 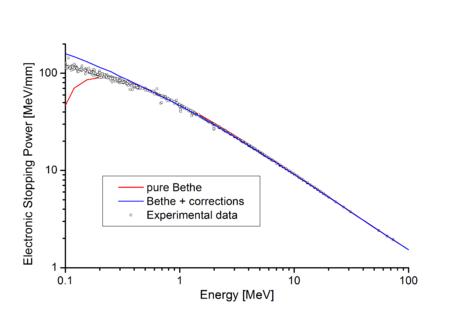 ターゲット物質の電子密度は以下の式で計算できる。 上式の ρ は材料の密度、Z と A はそれぞれ材料の原子番号と相対原子質量、NA はアボガドロ数、Mu はモル質量定数である。 右に示すグラフでは、小さい白丸が複数の著者による実験値を、赤い曲線はベーテの式を表している[4]。ベーテ理論は高エネルギー領域で実験と非常によく一致していることが明らかである。理論に修正を加えるとさらに良い一致が得られる(後述)。 エネルギーが低い、すなわち粒子速度が小さい (β ≪ 1) 場合には、ベーテの式は以下のように単純化される。 (2) 式 (1) の βc を v で置き換え、さらに β2 は微小なので無視すると上式が得られる。 式 (2) からわかるように、ベーテの式で表されるエネルギー損失は、低エネルギー領域においてはエネルギーの増加とともにほぼ v−2 に比例して減少し、およそ E = 3Mc2 で最小値に達する。この M は粒子の質量である(粒子が陽子なら M は約3000 MeVになる)。その先の領域 (β ≈ 1) では相対論効果が強くなり、エネルギー損失はエネルギーの増加とともに対数的に増加する。 平均励起ポテンシャル ベーテの理論では、材料の性質は平均励起ポテンシャル I という一つの量のみで表される。フェリックス・ブロッホは1933年に原子の平均イオン化ポテンシャルが近似的に以下で与えられることを示した。 (3) ここで Z は材料原子の原子番号である。この近似を前述の式 (1) に導入すると、一般にベーテ・ブロッホの式と呼ばれる表式が得られる。しかし、現在では Z に対して I を与える正確なテーブルが作られており、式 (3) の代わりにそれを使えばもっと良い結果が得られる。 あるテーブルから取得した I の値(規格化されている)を右図に示す[5]。このグラフで山(谷)になっている箇所では、阻止能のグラフが谷(山)になる。これは「Z2-振動」もしくは「Z2-構造」と呼ばれている( Z2 はターゲット物質の原子番号を意味する)。 ベーテ式の補正ベーテの式は量子力学的な摂動論によって導かれたため、粒子電荷 z の2乗に比例している。z の高次項にあたる補正を加えると結果はさらに改善される。そのような補正にはバルカス・アンダーソン効果( z3 に比例)やブロッホ補正( z4 に比例)がある。また、媒質物質の原子に含まれる電子が静止していないことを考慮した補正もある(殻補正)。 陽子やアルファ粒子の阻止能を計算することが可能なPSTARやASTARなどのプログラムにはこれらの補正が組み込まれている[6]。補正項は低エネルギーでは大きく、エネルギーが増加するにつれて小さくなる。 非常にエネルギーが高い領域では、フェルミの密度効果による補正[5]も加える必要がある。 名称の問題アメリカ国立標準技術研究所はPSTARやASTARの解説で式 (1) を "Bethe's stopping power formula"(ベーテの阻止能公式)と呼んでいる[6]。 パーティクル・データ・グループが公刊している総説 Review of Particle Physics では、ブロッホの近似式 (3) が用いられていないにもかかわらず "Bethe-Bloch equation"(ベーテ・ブロッホ方程式)の名が2008年の版まで使われた[7]。しかし後年の版で "Bethe formula"(ベーテの式)に変えられた[8][9]。 関連項目参照資料
外部リンク
|
![{\displaystyle -\left\langle {\frac {dE}{dx}}\right\rangle ={\frac {4\pi }{m_{\mathrm {e} }c^{2}}}\cdot {\frac {nz^{2}}{\beta ^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{\mathrm {e} }c^{2}\beta ^{2}}{I\cdot (1-\beta ^{2})}}\right)-\beta ^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88d990c714170430f5717e851119f4fc0b5ef78e)

![{\displaystyle -{\frac {dE}{dx}}={\frac {4\pi nz^{2}}{m_{\mathrm {e} }v^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{\mathrm {e} }v^{2}}{I}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fffcc7c8a4ef6231a0419c556573380553e0cfa7)
