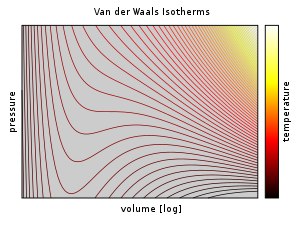
ファン・デル・ワールスの式による等温線 ファン・デル・ワールスの状態方程式 (ファン・デル・ワールスのじょうたいほうていしき、英語 : van der Waals equation )とは、実在気体 を表現する状態方程式 の一つである。1873年 にヨハネス・ファン・デル・ワールス により提案された。
ファン・デル・ワールスの状態方程式は、実在気体の理想気体 からのずれを二つのパラメータを導入することで表現している。二つのパラメータを導入する簡単な補正ではあるが、ジュール=トムソン効果 や気相 -液相 の相転移 について期待される振る舞いを再現できる上、解析的扱いが易しいため頻繁に用いられる。ただし、あくまで一つの理論モデルであり、厳密に実在気体の振る舞いを表現できる訳ではない。また、二つのパラメータだけで理想気体からのずれを表現しているため、ビリアル方程式 のように系統的に近似の精度を上げていく事が出来ない欠点もある。
ファン・デル・ワールスの状態方程式においては、熱力学温度 T 、モル体積 V m 圧力 が
p
=
R
T
V
m
−
b
−
a
V
m
2
{\displaystyle p={\frac {RT}{V_{\text{m}}-b}}-{\frac {a}{{V_{\text{m}}}^{2}}}}
で表される。係数 a,b は実在気体の理想気体からのずれを表現するパラメータで気体の種類ごとに定まり、ファン・デル・ワールス定数 と呼ばれる。
より実験を再現するように R もパラメータとすることも出来るが、低密度領域 a /RTV m ≪ 1b /V m ≪ 1R をモル気体定数 と等しく選ぶ。
ファン・デル・ワールス方程式から得られる偏微分は
(
∂
p
∂
T
)
V
=
R
V
m
−
b
{\displaystyle \left({\frac {\partial p}{\partial T}}\right)_{V}={\frac {R}{V_{\text{m}}-b}}}
(
∂
V
m
∂
T
)
p
=
V
m
−
b
T
/
[
1
−
2
a
R
T
V
m
⋅
(
1
−
b
V
m
)
2
]
{\displaystyle \left({\frac {\partial V_{\text{m}}}{\partial T}}\right)_{p}={\frac {V_{\text{m}}-b}{T}}{\bigg /}\left[1-{\frac {2a}{RTV_{\text{m}}}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right)^{2}\right]}
である。
これらの偏微分から熱膨張係数 α と等温圧縮率 κT が
α
=
1
T
⋅
(
1
−
b
V
m
)
/
[
1
−
2
a
R
T
V
m
⋅
(
1
−
b
V
m
)
2
]
{\displaystyle \alpha ={\frac {1}{T}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right){\bigg /}\left[1-{\frac {2a}{RTV_{\text{m}}}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right)^{2}\right]}
κ
T
=
V
m
R
T
⋅
(
1
−
b
V
m
)
2
/
[
1
−
2
a
R
T
V
m
⋅
(
1
−
b
V
m
)
2
]
{\displaystyle \kappa _{T}={\frac {V_{\text{m}}}{RT}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right)^{2}{\bigg /}\left[1-{\frac {2a}{RTV_{\text{m}}}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right)^{2}\right]}
と得られる。
統計力学 において、理想気体は運動エネルギー のみを持つ点粒子の系として再現される。言い換えれば、気体を構成する分子に体積がなく、分子間の相互作用 がない系として扱われる。しかし、現実の気体の分子には体積があり、分子間相互作用も存在する。
分子を点粒子ではなく古典的 な剛体 球 と考えると、同じ空間を複数の分子が占有することができない。これは体積排除効果 と呼ばれる。係数 b は排除体積効果に由来するパラメータである。圧力が無限大の極限 p →∞V m →b
一方、係数 a は分子間引力(ファンデルワールス力 )の効果を表現している。分子が互いに引き合うために、気体が容器を押す圧力は小さくなる。一つの分子による引力の効果は隣接する分子の数に比例し、それが分子ごとにあるので、全体としては体積当たりの分子数(密度)の二乗に比例すると考えることができる[ 1]
気体分子間の平均的な間隔が大きいほど、排除体積の影響も相互作用の影響も小さくなるため、低密度の極限では実在気体は理想気体のように振る舞う。理想気体の状態方程式は高温あるいは10atm以下の低圧ではかなり有効である。その傾向は気体の種類によっても異なり、同一気体については低温、高圧であるほどそのずれが大きくなる。
実在気体の理想気体からのずれは、しばしば圧縮率因子 を用いて表される。圧縮率因子を測定してプロットすることでファン・デル・ワールス定数 a,b を決定することが出来る。ファン・デル・ワールス方程式から圧縮率因子 z を計算すると
z
=
p
R
T
ρ
=
1
1
−
b
ρ
−
a
ρ
R
T
{\displaystyle z={\frac {p}{RT\rho }}={\frac {1}{1-b\rho }}-{\frac {a\rho }{RT}}}
となる。ρ = 1/V m ビリアル展開 すれば
z
=
1
+
(
b
−
a
R
T
)
ρ
+
b
2
ρ
2
+
b
3
ρ
3
+
⋯
{\displaystyle z=1+\left(b-{\frac {a}{RT}}\right)\rho +b^{2}\rho ^{2}+b^{3}\rho ^{3}+\cdots }
となり、ビリアル係数として
A
2
=
b
−
a
R
T
,
A
3
=
b
2
,
A
4
=
b
3
,
…
{\displaystyle A_{2}=b-{\frac {a}{RT}},~A_{3}=b^{2},~A_{4}=b^{3},\ldots }
が得られる。ファン・デル・ワールス方程式から得られるビリアル係数は第2ビリアル係数を除いて温度に依存しない。
各温度における第2ビリアル係数を実験的に求めれば、温度に依存する部分と定数部分とから、ファン・デル・ワールス定数 a,b を決定する事ができる。
また、第2ビリアル係数がゼロとなるボイル温度 は
T
B
=
a
b
R
=
27
8
T
c
{\displaystyle T_{\text{B}}={\frac {a}{bR}}={\frac {27}{8}}T_{\text{c}}}
で与えられる。
実在気体の等温線の模式図 ファン・デル・ワールス方程式の有用性の一つとして、気相 -液相 間の相転移 を表現できることが挙げられる。
熱力学から導かれる制約により等温圧縮率 κT は常に正であり、不等式
1
−
2
a
R
T
V
m
⋅
(
1
−
b
V
m
)
2
>
0
{\displaystyle 1-{\frac {2a}{RTV_{\text{m}}}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right)^{2}>0}
が得られる。この不等式が満たされる体積の範囲は、右図の等温線のうち極小点 A と極大点 C の外側の実線の部分である。
このうち、安定的な平衡状態に相当するのは点 F と点 G の外側の青色の実線の部分と、点 F と点 G の間のを直線部分である。
点 F の左側が液相に相当し、点 G の右側が気相に相当する。直線部分は気相と液相が共存する状態である。
緑色の実線部分は準安定 な状態であり、点 F から極小点 A までの間は過熱 、点 G から極大点 C までの間は過冷却 に相当する。
不等式が成り立たない極小点 A と極大点 C の内側の破線部は非物理的な状態である。
ファン・デル・ワールス方程式の臨界点 は等温線の極小点 A と極大点 C が接近して消失する点 K を求めることで得られる。ファン・デル・ワールス方程式に基づいて計算される臨界温度 T c p c V c a,b と
T
c
=
8
a
27
b
R
,
p
c
=
a
27
b
2
,
V
c
=
3
b
{\displaystyle T_{\text{c}}={\frac {8a}{27bR}},~p_{\text{c}}={\frac {a}{27b^{2}}},~V_{c}=3b}
の関係にある[ 3]
臨界定数の式を逆に解けば
a
=
3
p
c
V
c
2
,
b
=
V
c
3
,
R
=
8
p
c
V
c
3
T
c
{\displaystyle a=3p_{\text{c}}{V_{\text{c}}}^{2},~b={\frac {V_{\text{c}}}{3}},~R={\frac {8p_{\text{c}}V_{\text{c}}}{3T_{\text{c}}}}}
として臨界定数から状態方程式のパラメータを決定することができる。ここでは係数 R を臨界定数から求められる調整パラメータとして扱っている。
ただし、ファン・デル・ワールス方程式はあくまで近似式であるため、臨界定数から計算した R がモル気体定数と厳密には一致しない[ 1] R をモル気体定数に固定する場合は、臨界体積が
V
c
calc
=
3
R
T
c
8
p
c
{\displaystyle V_{\text{c}}^{\text{calc}}={\frac {3RT_{\text{c}}}{8p_{\text{c}}}}}
によって求められるとみなせば、ファン・デル・ワールス定数 a,b は
a
=
3
p
c
(
V
c
calc
)
2
=
27
R
2
T
c
2
64
p
c
{\displaystyle a=3p_{\text{c}}(V_{\text{c}}^{\text{calc}})^{2}={\frac {27R^{2}{T_{\text{c}}}^{2}}{64p_{\text{c}}}}}
b
=
1
3
V
c
calc
=
R
T
c
8
p
c
{\displaystyle b={\frac {1}{3}}V_{\text{c}}^{\text{calc}}={\frac {RT_{\text{c}}}{8p_{\text{c}}}}}
で決定される。
主な気体の臨界定数、およびファンデルワールス定数[ 3]
気体
T c p c V c 3 mol−1
a / Pa m6 mol−2 b / m3 mol−1
空気
132.5
3.766× 10
88.1× 10−6
135× 10−3
36.6× 10−6
ヘリウム He
5.201
0.227× 10
57.5× 10−6
3.45× 10−3
23.8× 10−6
水素 H2
33.2
1.316× 10
63.8× 10−6
24.8× 10−3
26.7× 10−6
窒素 N2
126.20
3.400× 10
89.2× 10−6
141× 10−3
39.2× 10−6
酸素 O2
154.58
5.043× 10
73.4× 10−6
138× 10−3
31.9× 10−6
二酸化炭素 CO2
304.21
7.383× 10
94.4× 10−6
365× 10−3
42.8× 10−6
水蒸気 H2 O
647.30
22.12× 10
57.1× 10−6
553× 10−3
33.0× 10−6
臨界定数によって各変数を
τ
=
T
/
T
c
,
π
=
p
/
p
c
,
ϕ
=
V
m
/
V
c
{\displaystyle \tau =T/T_{\text{c}},~\pi =p/p_{\text{c}},~\phi =V_{\text{m}}/V_{\text{c}}}
によって規格化すると、状態方程式は
π
=
8
τ
3
ϕ
−
1
−
3
ϕ
2
{\displaystyle \pi ={\frac {8\tau }{3\phi -1}}-{\frac {3}{\phi ^{2}}}}
となる[ 4] 無次元化 された温度、圧力、体積により、状態方程式が気体の種類によらず同一の形で表されること[ 5] 還元方程式 (reduced form of equation of state )と呼ばれる。
圧力がファン・デル・ワールスの状態方程式に従うとき、内部エネルギー は理想気体と異なり、体積にも依存する。
これは熱力学的状態方程式
(
∂
U
∂
V
)
T
=
T
(
∂
p
∂
T
)
V
−
p
=
a
V
m
2
{\displaystyle \left({\frac {\partial U}{\partial V}}\right)_{T}=T\left({\frac {\partial p}{\partial T}}\right)_{V}-p={\frac {a}{{V_{\text{m}}}^{2}}}}
から導かれる。
気体の振る舞いは状態方程式だけでは決まらず、熱容量に関する情報が必要である。特に等積モル熱容量 が理想気体と同じく定数 cv = cR ファン・デル・ワールス気体 と呼ぶことがある。
ファン・デル・ワールス気体のモル内部エネルギーは
U
m
=
μ
∗
+
c
R
T
−
a
V
m
{\displaystyle U_{\text{m}}=\mu ^{*}+cRT-{\frac {a}{V_{\text{m}}}}}
となり、モルエントロピー は
S
m
=
c
R
ln
T
T
∗
+
R
ln
V
m
−
b
R
T
∗
/
p
∘
=
c
R
ln
U
m
−
μ
∗
+
a
/
V
m
c
R
T
∗
+
R
ln
V
m
−
b
R
T
∗
/
p
∘
{\displaystyle {\begin{aligned}S_{\text{m}}&=cR\ln {\frac {T}{T^{*}}}+R\ln {\frac {V_{\text{m}}-b}{RT^{*}/p^{\circ }}}\\&=cR\ln {\frac {U_{\text{m}}-\mu ^{*}+a/V_{\text{m}}}{cRT^{*}}}+R\ln {\frac {V_{\text{m}}-b}{RT^{*}/p^{\circ }}}\end{aligned}}}
となる。エネルギーと体積を変数として表したエントロピーは完全な熱力学関数 であり、ファン・デル・ワールス気体の総ての情報を持っている。
分子間の引力効果について、気体の1分子が持つ相互作用の有効範囲である体積を V 0 、 V 0 の物質量を N 0 とすると, N 0 個の分子から、2つの分子間の相互作用の組み合わせは、
N
0
C
2
=
N
0
!
(
N
0
−
2
)
!
2
!
=
N
0
(
N
0
−
1
)
2
=
N
0
2
2
=
1
2
n
2
V
0
2
V
2
=
V
0
2
2
×
(
n
V
)
2
{\displaystyle {\begin{aligned}{}_{N_{0}}{\rm {C}}_{2}&={\frac {N_{0}!}{(N_{0}-2)!2!}}={N_{0}(N_{0}-1) \over 2}\\&={N_{0}^{2} \over 2}={\frac {1}{2}}n^{2}{\frac {V_{0}^{2}}{V^{2}}}\\&={V_{0}^{2} \over 2}\times \left({n \over V}\right)^{2}\end{aligned}}}
である。個々の分子が容器に及ぼす圧力は、壁と分子の衝突の頻度および分子によって壁に伝えられる運動量に依存する。どちらも分子間力によって減少する。この式から、圧力の減少分は、V 0 と密度 n /V に依存することが分かる。ここで
a
=
V
0
2
2
{\displaystyle a={V_{0}^{2} \over 2}}
と定義すると、a は分子の種類によって定まる比例定数である。a は b と共にファンデルワールス定数と呼ばれる。
ファン・デル・ワールスの状態方程式を修正した状態方程式が提案されている[ 6]
Berthelot:
(
p
+
a
T
V
2
)
(
V
−
b
)
=
R
T
{\displaystyle \left(p+{\frac {a}{TV^{2}}}\right)(V-b)=RT}
Redlich-Kwong:
(
p
+
a
T
1
/
2
V
(
V
+
b
)
)
(
V
−
b
)
=
R
T
{\displaystyle \left(p+{\frac {a}{T^{1/2}V(V+b)}}\right)(V-b)=RT}



![{\displaystyle \left({\frac {\partial V_{\text{m}}}{\partial T}}\right)_{p}={\frac {V_{\text{m}}-b}{T}}{\bigg /}\left[1-{\frac {2a}{RTV_{\text{m}}}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37e4db670333748f7369cb5f7c76841bf4fe1c12)
![{\displaystyle \alpha ={\frac {1}{T}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right){\bigg /}\left[1-{\frac {2a}{RTV_{\text{m}}}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65c4fd5f67d37c9b35b178e94d4e3da99c2a977f)
![{\displaystyle \kappa _{T}={\frac {V_{\text{m}}}{RT}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right)^{2}{\bigg /}\left[1-{\frac {2a}{RTV_{\text{m}}}}\cdot \left(1-{\frac {b}{V_{\text{m}}}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adc2f9644b28ae31fed44098086c537049ca5566)


















