|
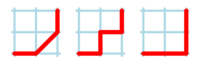
Numero di Schröder-IpparcoIn matematica, data una griglia quadrata di dimensione nel 1° quadrante di un sistema di riferimento cartesiano, il numero di Schröder-Ipparco, , descrive il numero di cammini possibili per arrivare dal punto di coordinate al punto di coordinate , ammettendo di potersi muovere soltanto in verticale e in orizzontale o in diagonale verso destra e senza che il cammino oltrepassi mai la diagonale data dalla retta di equazione o abbia passi che corrono lungo di essa. I numeri di Schröder-Ipparco sono detti anche piccoli numeri di Schröder e differiscono dai "grandi numeri di Schröder" per il fatto che questi ultimi tengono anche conto dei cammini che non aderiscono all'ultima delle condizioni sopra elencate. La successione di tali numeri interi, che prendono il nome dal matematico tedesco Ernst Schröder e dall'antico matematico greco Ipparco di Nicea, che ci è noto conoscesse tali numeri, per , ha come primi elementi:
Applicazioni in combinatoria In combinatoria la successione dei numeri di Schröder-Ipparco può essere utilizzata in diversi oggetti relativi a tale branca della matematica:[2][3][4] 
Come mostrato in figura, c'è una semplice equivalenza combinatoria tra questi oggetti: la suddivisione di un poligono ha un albero ordinato come forma del proprio grafo duale, e in tale albero, le foglie corrispondono ai simboli in una successione parentesizzata mentre i nodi interni, ma non la radice, corrispondono ai gruppi parentesizzati. La successione parentesizzata stessa può essere scritta lungo il perimetro del poligono con i suoi simboli lungo i lati del poligono e le parentesi agli estremi delle diagonali scelte. Ciò equivale a dare una dimostrazione mediante biiezione del fatto che tutti questi generi di oggetti possono essere conteggiati attraverso un'unica successione di interi.[2] La successione enumera poi anche il numero di permutazioni doppie, ossia successioni di numeri che vanno da a , in cui ogni numero appare due volte e in cui la prima apparizione di ogni numero avviene in ordine crescente, che evitano gli schemi 12312 e 121323.[5] Successioni correlateI numeri della già citata successione dei numeri grandi di Schröder sono pari a due volte i numeri di Schröder-Ipparco, e possono anch'essi essere utilizzati per conteggiare diversi oggetti trattati in combinatoria, essi rappresentano ad esempio il numero di modi in cui si può dividere un rettangolo in rettangoli più piccoli usando segmenti passanti per punti disposti in maniera casuale nel rettangolo, con ogni segmento che interseca uno solo dei suddetti punti e divide solo un singolo rettangolo in due più piccoli. Un'altra successione di interi correlata ai numeri di Schröder-Ipparco è quella dei numeri di Catalan, che rappresentano, tra le altre cose, il numero di modi in cui un poligono convesso con lati può essere suddiviso in triangoli e il numero di modi in cui si possono inserire coppie di parentesi in una successione di simboli in modo tale che ogni coppia circondi esattamente due simboli o due gruppi già circondati da parentesi.[3] Data una successione di operatori lineari naturalmente definiti su successioni di interi, se viste come vettori riga di dimensione infinita, la successione dei numeri di Catalan e quella dei numeri di Schröder-Ipparco sono gli unici autovettori dei primi due elementi di tale successione.[6][7] Più in generale la -sima successione in questa successione di successioni di interi è , dove i numeri sono calcolati come somme di numeri di Narayana moltiplicati per potenze di . Ciò può essere espresso come una funzione ipergeometrica: Ponendo in tale equazione si ottiene la successione dei numeri di Catalan, mentre ponendo si ottiene la successione dei numeri di Schröder-Ipparco.[7] RicorrenzaCosì come la sommatoria precedentemente citata, la successione dei numeri di Schröder-Ipparco può essere definita da una relazione di ricorrenza: Ciò è stato dimostrato da Richard P. Stanley utilizzando delle funzioni generatrici[8] mentre Dominique Foata e Doron Zeilberger hanno fornito una diretta prova combinatoria.[9] StoriaNei Moralia di Plutarco, l'autore racconta di un dialogo avvenuto tra il filosofo Stoico Crisippo di Soli, che sosteneva che le proposizioni composte che si potevano fare con solo 10 proposizioni fossero più di un milione, e l'astronomo Ipparco di Nicea, suo contemporaneo. In particolare il brano recita:[10] "Crisippo dice che il numero di proposizioni composte che possono essere formate a partire da dieci sole proposizioni supera il milione. Ipparco dimostrò però che tale numero è 103049 in senso affermativo (ossia utilizzando solo i connettivi "e" e "o") e 310952 in senso negativo (ossia ammettendo anche l’uso della negazione)". Tale scritto rimase senza spiegazione fino al 1994, quando David Hough, della George Washington University, osservò che c'erano 103 049 modi di inserire parentesi in una successione di 10 elementi, essendo in effetti il decimo numero della successione di Schröder-Ipparco.[11] Per quanto riguarda il numero 310 952, la sua interpretazione resta oscura, tuttavia sebbene tale numero non appaia nelle sequenze di numeri legate alla matematica combinatoria note, lo storico della matematica Fabio Acerbi (CNRS) ha mostrato come esso sia pari alla media del decimo e dell'undicesimo numero di Schröder-Ipparco meno due, ed è pari al numero di modi in cui si possono inserire due parentesi in una successione di dieci termini assieme a una particella negativa.[11] Nel 2011 la filosofa Susanne Bobzien ha obiettato che, sulla base della logica Stoica, un sistema di logica proposizionale sviluppato dagli Stoici, fosse il calcolo di Crisippo ad essere quello giusto. Ricostruendo i calcoli fatti da Ipparco e da Crisippo, la Bobzien sostiene che l'aver mostrato l'esattezza matematica del calcolo di Ipparco ma la sua inesattezza logica potrebbe gettare nuova luce sulle nozioni stoiche di congiunzioni e asseribili.[12] Note
Voci correlateAltri progetti
Collegamenti esterni
|