|
How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension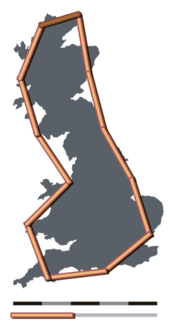 Lunghezza = ~2400 km  Lunghezza = ~3400 km How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension è un articolo scientifico pubblicato dal matematico polacco-francese Benoît Mandelbrot su Science nel 1967.[1] Nell'articolo Mandelbrot studia l'autosimilarità tra curve con dimensione di Hausdorff compresa tra 1 e 2: tali curve sono esempi di frattali, anche se Mandelbrot nella pubblicazione non usa il termine, che verrà introdotto solo nel 1975. L'articolo è una delle prime pubblicazioni di Mandelbrot riguardante i frattali.[2] L'articolo è importante in quanto rappresenta un punto di svolta nel primo approccio di Mandelbrot allo studio dei frattali,[3] ed è un esempio di collegamento tra oggetti matematici e forme naturali che caratterizzerà buona parte del suo lavoro successivo. ContenutiL'articolo esamina il paradosso della linea costiera, ovvero il fatto che la lunghezza della linea costiera dipende dalla scala sulla quale viene misurata, ed empiricamente aumenta quando si riduce l'ampiezza dell'unità di misura di riferimento. Ad esempio, misurando una curva con una riga lunga un metro, la misura sarà in genere minore rispetto alla stessa misura effettuata con un righello da 30 cm. Come conseguenza di questo fatto, non ha significato parlare in senso assoluto di lunghezza della linea costiera, ma è necessario introdurre un modo più specifico per definire il concetto. Mandelbrot discute una legge empirica scoperta da Lewis Fry Richardson, il quale osserva che la lunghezza misurata L(G) è una funzione della scala di misura G. In base a dati sperimentali raccolti da differenti esempi, Richardson congetturava che L(G) poteva essere approssimata con una funzione nella forma dove M è una costante positiva e D è una costante, chiamata dimensione, maggiore o uguale a 1. Intuitivamente, se una linea costiera appare liscia deve avere una dimensione prossima a 1, mentre una linea costiera molto irregolare deve avere dimensione prossima a 2. Gli esempi proposti da Richardson hanno dimensione che va dallo 1,02 delle coste del Sudafrica fino all'1,25 per la costa occidentale della Gran Bretagna. Mandelbrot quindi descrive varie curve, correlate alla curva di Koch, definite in maniera da essere strettamente autosimili, quindi mostra come calcolarne la dimensione di Hausdorff, che in ogni esempio ha un valore compreso tra 1 e 2. Mandelbrot cita anche una curva di Peano che ha dimensione esattamente 2, senza mostrarne la costruzione. Osserva quindi che l'approssimazione di tali curve con segmenti di lunghezza G ha una lunghezza nella forma , notevolmente somigliante alla legge di Richardson. Nell'articolo Mandelbrot non sostiene mai che le linee costiere hanno una effettiva dimensione frattale, ma osserva che la legge empirica di Richardson è compatibile con l'idea che i contorni geografici possano essere modellizzati con curve autosimili casuali di dimensione frattale. Verso la fine dell'articolo Mandelbrot discute brevemente un possibile approccio allo studio di oggetti naturali simil-frattali il cui aspetto è più casuale che regolare, definendo allo scopo figure statisticamente autosimili. Note
Voci correlateCollegamenti esterni
|

