Figura isogonale

In geometria, un politopo (un poligono, un poliedro o una tassellatura, per esempio) è isogonale o transitivo sui vertici se tutti i suoi vertici sono equivalenti rispetto alle simmetrie della figura. Ciò implica che ogni vertice è circondato dagli stessi tipi di facce nello stesso ordine o in ordine inverso e con gli stessi angoli tra le facce corrispondenti.

Tecnicamente, si dice che per due vertici qualsiasi esiste una simmetria del politopo che mappa il primo isometricamente sul secondo. Altri modi per dirlo sono che il gruppo di automorfismi del politopo agisce transitivamente sui suoi vertici, o che i vertici giacciono all'interno di un'unica orbita di simmetria.

Tutti i vertici di una figura isogonale n-dimensionale finita esistono su (n−1)-sfere. 

Il termine isogonale è stato a lungo usato per indicare questo tipo di poliedri. Transitivo sui vertici è un sinonimo preso in prestito da idee moderne come i gruppi di simmetria e la teoria dei grafi.

Il caso dello pseudorombicubottaedro – che non è isogonale – dimostra che la più semplice condizione che "tutti i vertici sembrino uguali" non è altrettanto restrittiva rispetto alla definizione utilizzata qui, che coinvolge il gruppo di isometrie che preservano il poliedro o la tassellatura.

Poligoni isogonali e apeirogoni

Apeirogoni isogonali
Apeirogoni sghembi isogonali

Tutti i poligoni regolari, gli apeirogoni e i poligoni stellari regolari sono isogonali. Il duale di un poligono isogonale è un poligono isotossale.

Alcuni poligoni e apeirogoni con un numero pari di lati la cui lunghezza si alterna tra due possibilità, ad esempio un rettangolo, sono isogonali.

Tutti i 2 n-goni isogonali planari hanno simmetria diedrica (D_n, n = 2, 3, ...) con linee di riflessione passanti per i punti medi dei lati.

D 2	D 3	D 4	D 7
Rettangoli isogonali e rettangoli incrociati che condividono la stessa disposizione dei vertici	Esagramma isogonale con 6 vertici identici e 2 lunghezze dei lati.[1]	Ottagono convesso isogonale con linee di riflessione radiali blu e rosse	Tetradecagono a "stella" isogonale con un tipo di vertice e due tipi di spigoli[2]

Poliedri isogonali e tassellature bidimensionali

Tassellazioni isogonali

Una tassellazione quadrata distorta

Una tassellazione quadrata troncata distorta

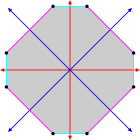
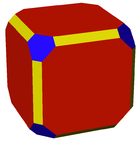
Un poliedro isogonale e una tassellatura bidimensionale hanno un unico tipo di vertice. Un poliedro isogonale, con tutte le facce regolari, è anche un poliedro uniforme e può essere rappresentato usando la notazione di incidenza dei vertici che sequenzia le facce attorno a ciascun vertice. Questa notazione può anche usata anche per variazioni geometricamente distorte di poliedri e tassellature uniformi.

Poliedri isogonali

D3d, ordine 12	Th, ordine 24	Oh, ordine 48
4.4.6	3.4.4.4	4.6.8	3.8.8
Un prisma esagonale distorto (trapezoprisma ditrigonale)	Un rombicubottaedro distorto	Cubottaedro troncato poco profondo	Un cubo ipertroncato

I poliedri isogonali e le tassellature bidimensionali possono essere ulteriormente classificati:

• Regolare se è anche isoedrico (transitivo sulle facce) e isotossale (transitivo sugli spigoli); questo implica che ogni faccia è dello stesso tipo di poligono regolare.
• Quasi regolare se è anche isotossale (transitivo sulle facce) ma non isoedrico (transitivo sugli spigoli).
• Semiregolare se ogni faccia è un poligono regolare ma non è isoedrico o isotossale. (La definizione varia tra gli autori; ad esempio, alcuni escludono i solidi con simmetria diedrica o i solidi non convessi.)
• Uniforme se ogni faccia è un poligono regolare, cioè regolare, quasi regolare o semiregolare.
• Semiuniforme se i suoi elementi sono anche isogonali.
• Scaliforme se tutti gli spigoli sono della stessa lunghezza.
• Nobile se è anche isoedrico.

Dimensioni N: politopi isogonali e tassellazioni

Queste definizioni possono essere estese a politopi e tassellazioni di dimensioni superiori. Tutti i politopi uniformi sono isogonali, ad esempio i policori uniformi e i favi uniformi convessi.

Il duale di un politopo isogonale è una figura isoedrica, transitiva nelle sue facet.

Figure k-isogonali e k-uniformi

Un politopo o una tassellatura può essere chiamata k-isogonale se i suoi vertici formano k classi di transitività. Un termine più restrittivo, k-uniforme, è definito come una figura k-isogonale costruita solo da poligoni regolari. Possono essere rappresentati visivamente con colori di diverse colorazioni uniformi.

Questo dodecaedro rombico troncato è 2-isogonale perché contiene due classi di transitività sui vertici. Questo poliedro è formato da quadrati ed esagoni appiattiti.

Questa tassellatura semiregolare è anche 2-isogonale (e 2-uniforme). Questa piastrellatura è composta da triangolo equilatero e facce esagonali regolari.

Enneagramma 2-isogonale 9/4 (faccia della stellazione finale dell'icosaedro)

Note

1. Coxeter, The Densities of the Regular Polytopes II, p54-55, "hexagram" vertex figure of h{5/2,5}.
2. The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum, Figure 1. Parameter t=2.0

Bibliografia

• Peter R. Cromwell, Poliedri, Cambridge University Press 1997,ISBN 0-521-55432-2, pag. 369 Transitività