N-gramme

Un n-gramme est une sous-séquence de n éléments construite à partir d'une séquence donnée. L'idée semble provenir des travaux de Claude Shannon en théorie de l'information. Son idée était que, à partir d'une séquence de lettres donnée (par exemple « par exemple ») il est possible d'obtenir la fonction de vraisemblance de l'apparition de la lettre suivante. À partir d'un corpus d'apprentissage, il est facile de construire une distribution de probabilité pour la prochaine lettre avec un historique de taille ${\displaystyle n}$. Cette modélisation correspond en fait à un modèle de Markov d'ordre ${\displaystyle n}$ où seules les ${\displaystyle n}$ dernières observations sont utilisées pour la prédiction de la lettre suivante. Ainsi un bigramme est un modèle de Markov d'ordre 2.

À titre d'exemple, le bi-gramme le plus fréquent de la langue française est « de », comme dans l'article « de », mais aussi comme dans les mots « demain », « monde » ou « moderne ». En traitement du langage naturel il est fréquent de parler de N-gramme pour désigner des séquences de mots et non de lettres.

Exemple

À partir du (court) corpus « par exemple », nous obtenons :

Pas d'historique (unigramme) :

• p : 2 occurrences sur 10 lettres = 2/10 ;
• e : 3 occurrences sur 10 lettres = 3/10 ;
• x : 1 occurrence sur 10 lettres = 1/10 ;

... La somme des probabilités étant nécessairement égale à 1.

Historique de taille 1 (on considère la lettre et un successeur) :

• p-a : 1 occurrence sur 9 couples = 1/9 ;
• p-l : 1 occurrence sur 9 couples = 1/9 ;
• p-e : 0 occurrence sur 9 couples = 0 ;

... La somme des probabilités étant toujours nécessairement égale à 1.

Nous obtenons des probabilités conditionnelles nous permettant de connaître, à partir d'une sous-séquence, la probabilité de la sous-séquence suivante. Dans notre exemple, ${\displaystyle P(a|p)=1/2}$ est la probabilité d'apparition de l'élément a sachant que l'élément p est apparu.

Usage des N-grammes

Les N-grammes sont beaucoup utilisés en traitement automatique du langage naturel mais aussi en traitement du signal. Leur utilisation repose sur l'hypothèse simplificatrice que, étant donné une séquence de k éléments (${\displaystyle k\geq n}$) la probabilité de l'apparition d'un élément en position i ne dépend que des n-1 éléments précédents.

On a donc ${\displaystyle P(w_{i}|w_{1},...,w_{i-1})=P(w_{i}|w_{i-(n-1)},w_{i-(n-2)},...,w_{i-1})}$.

Avec ${\displaystyle n=3}$ (cas du trigramme), on a ${\displaystyle P(w_{i}|w_{1},...,w_{i-1})=P(w_{i}|w_{i-2},w_{i-1})}$.

La probabilité de la séquence : ${\displaystyle P(w_{1,k})=P(w_{1})\times P(w_{2}|w_{1})\times P(w_{3}|w_{1},w_{2})\times ...\times P(w_{k}|w_{1},w_{2}...w_{k-1})}$

est transformée en : ${\displaystyle P(w_{1,k})=P(w_{1})\times P(w_{2}|w_{1})\prod _{i=3}^{n}P(w_{i}|w_{i-2},w_{i-1})}$ (on notera les deux premiers termes conservés, il n'y a en effet pas d'élément en position 0 et -1 de la séquence. Ceci peut-être corrigé en introduisant des termes vides, mais ça n'a que peu d'importance).

Entraînement des N-grammes

Partant de cette hypothèse, il est alors possible d'apprendre les n-grammes à partir d'un corpus. Avec ${\displaystyle n=3}$, il suffit de parcourir le corpus et de noter, pour chaque apparition d'un triplet d'élément (par exemple, pour chaque triplet de caractères ou de mots) le nombre d'apparitions de ce triplet, le nombre d'apparitions du couple en début de triplet et de diviser le premier par le second.

Sur un exemple simple, partant du corpus d'apprentissage « aabaacaab », nous avons les triplets suivants :

• aab
• aba
• baa
• aac
• aca
• caa
• aab

Dénombrons les :

• aab : 2 occurrences
• aba : 1 occurrence
• baa : 1 occurrence
• aac : 1 occurrence
• aca : 1 occurrence
• caa : 1 occurrence

Ainsi que les couples en début de triplet :

• aa : 3 occurrences
• ab : 1 occurrence
• ba : 1 occurrence
• ac : 1 occurrence
• ca : 1 occurrence

Nous obtenons les tri-grammes suivants :

• ${\textstyle P(b|aa)={\frac {P(aab)}{P(aa)}}={\frac {P(aab)}{\sum _{X\in \{a,b,c\}}P(aaX)}}={\frac {2/7}{0+2/7+1/7}}={\frac {2}{3}}}$
• ${\displaystyle P(c|aa)={\frac {P(aac)}{P(aa)}}=1/3}$
• ${\displaystyle P(a|ab)={\frac {P(aba)}{P(ab)}}=1}$
• ...

À partir de ce corpus, on déduit que, si le couple « aa » apparaît, alors la probabilité que l'élément suivant soit « b » est de 2/3, la probabilité que l'élément suivant soit « c » est de 1/3.

Une propriété triviale mais importante est ${\displaystyle \forall w_{i},w_{j},\sum _{k}P(w_{i},w_{j},w_{k})=\sum _{k}P(w_{k}|w_{i},w_{j})P(w_{i},w_{j})=P(w_{i},w_{j})\sum _{k}P(w_{k}|w_{i},w_{j})=P(w_{i},w_{j})}$. Ceci se généralise trivialement pour toute valeur de n.

Nous obtenons la chaîne de Markov équivalente :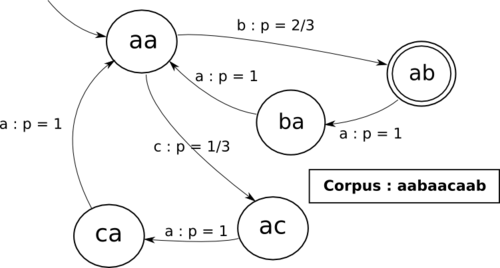

Limite des N-grammes

Un premier problème se pose : certains triplets n'apparaissent pas dans le corpus d'apprentissage (leur probabilité est donc fixée à 0) mais risquent d'apparaître à l'utilisation. En effet, on sait qu'il est impossible de construire un corpus représentatif contenant, de façon justement distribuée (c'est-à-dire correspondant à la distribution réelle) l'ensemble des n-grammes d'un langage^[réf. souhaitée] (par « langage », nous entendons ici une langue naturelle, mais par extension n'importe quel ensemble de séquences particulier que l'on voudrait soumettre à l'apprentissage par les n-grammes).

Pour pallier ce problème, les probabilités sont « lissées ». Le calcul du tri-gramme est approximé et devient :

${\displaystyle P(w_{n-2}w_{n-1}w_{n})=\lambda _{1}P(w_{n-2})\times \lambda _{2}P(w_{n-1}|w_{n-2})\times \lambda _{3}P(w_{n}|w_{n-2},w_{n-1})}$

avec ${\displaystyle \lambda _{1}+\lambda _{2}+\lambda _{3}=1}$, ${\displaystyle P(w_{n-2})}$ la probabilité de l'unigramme et ${\displaystyle P(w_{n-1}|w_{n-2})}$ la probabilité du bi-gramme.

Exploitation des N-grammes

Un exemple complet d'utilisation des N-grammes est présenté dans l'article Algorithme de Viterbi.

Voir aussi

• Algorithme de Viterbi pour un traitement efficace de l'information à l'aide de n-gramme.
• Modèle de Markov caché
• digramme
• Google Ngram Viewer affiche, par année, la fréquence d'une suite de mots dans un corpus de livres