Graphe de Tutte

Graphe de Tutte
Représentation du graphe de Tutte
Nombre de sommets	46
Nombre d'arêtes	69
Distribution des degrés	3-régulier
Rayon	5
Diamètre	8
Maille	4
Automorphismes	3 (Z/3Z)
Nombre chromatique	3
Indice chromatique	3
Propriétés	Régulier Cubique Planaire
modifier

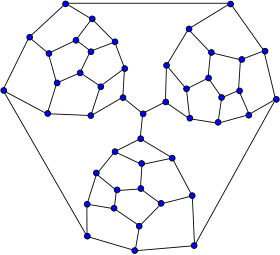
Le graphe de Tutte est, en théorie des graphes, un graphe 3-régulier possédant 46 sommets et 69 arêtes.

Histoire

Le graphe de Tutte est découvert par le mathématicien William Tutte en 1946. C'est le premier contre-exemple connu à la conjecture de Tait sur les graphes hamiltoniens, c'est-à-dire que c'est un graphe planaire non-hamiltonien étant 3-sommet-connexe[1],[2].

Le graphe de Tutte est suivi de la construction de plusieurs autres contre-exemples à cette conjecture. Notamment trois par Grinberg (le 46-graphe de Grinberg, le 44-graphe de Grinberg et le 42-graphe de Grinberg), et deux par Faulkner et Younger (le 44-graphe de Faulkner-Younger et le 42-graphe de Faulkner-Younger)[3],[4].

En 1965, Lederberg construit un contre-exemple à la conjecture de Tait doté de seulement 38 sommets : le graphe de Barnette-Bosák-Lederberg[5]. Lederberg émet l'hypothèse de sa minimalité mais est incapable de la prouver. Il démontre cependant qu'un contre-exemple minimal à la conjecture de Tait doit avoir strictement plus de 24 sommets.

À peu près à la même époque, David Barnette et Juraj Bosák (sk) construisent six contre-exemples d'ordre 38 à la conjecture de Tait, redécouvrant indépendamment le graphe de Barnette[6],[7].

En 1988, Derek Holton et Brendan McKay prouvent qu'il est impossible de construire un contre-exemple à la conjecture de Tait avec moins de 38 sommets. Dans le même article, ils démontrent que les 6 graphes décrits par D. Barnette et J. Bosák sont les seuls de cet ordre[8].

Propriétés

Propriétés générales

Le diamètre du graphe de Tutte, l'excentricité maximale de ses sommets, est 8, son rayon, l'excentricité minimale de ses sommets, est 5 et sa maille, la longueur de son plus court cycle, est 4. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.

Coloration

Le nombre chromatique du graphe de Tutte est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe.

L'indice chromatique du graphe de Tutte est 3. Il existe donc une 3-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.

Propriétés algébriques

Le groupe d'automorphismes du graphe de Tutte est un groupe abélien d'ordre 3 isomorphe au groupe cyclique Z/3Z.

Le polynôme caractéristique de la matrice d'adjacence du graphe de Tutte est :

${\displaystyle (x-3)(x^{15}-22x^{13}+x^{12}+184x^{11}-26x^{10}-731x^{9}+199x^{8}+1383x^{7}-576x^{6}-1061x^{5}+561x^{4}+233x^{3}-151x^{2}+4x+4)^{2}}$

${\displaystyle (x^{15}+3x^{14}-16x^{13}-50x^{12}+94x^{11}+310x^{10}-257x^{9}-893x^{8}+366x^{7}+1218x^{6}-347x^{5}-717x^{4}+236x^{3}+128x^{2}-56x+4).}$

Voir aussi

Liens internes

• Théorie des graphes

Liens externes

• (en) Eric W. Weisstein, « Tutte's Graph », sur MathWorld
• (en) Eric W. Weisstein, « Tait's Hamiltonian Graph Conjecture », sur MathWorld

Références

1. (en) P. G. Tait, « Listing's Topologie », Philosophical Magazine (5th ser.), vol. 17,‎ 1884, p. 30–46. Reprinted in Scientific Papers, Vol. II, pp. 85–98.
2. (en) W. T. Tutte, « On Hamiltonian circuits », Journal of the London Mathematical Society (2nd ser.), vol. 21, n^o 2,‎ 1946, p. 98–101 (lire en ligne)
3. (en) Faulkner, G. B. and Younger, D. H. "Non-Hamiltonian Cubic Planar Maps." Discr. Math. 7, 67-74, 1974.
4. Claude Berge, Graphes et hypergraphes, Dunod, 1973.
5. (en) Lederberg, J. "DENDRAL-64: A System for Computer Construction, Enumeration and Notation of Organic Molecules as Tree Structures and Cyclic Graphs. Part II. Topology of Cyclic Graphs." Interim Report to the National Aeronautics and Space Administration. Grant NsG 81-60. December 15, 1965. [1]
6. (en) Eric W. Weisstein, Barnette-Bosák-Lederberg Graph (MathWorld)
7. (en) Derek Holton and Robert E. L. Aldred. Planar Graphs, Regular Graphs, Bipartite Graphs and Hamiltonicity. Australasian Journal of Combinatorics, 20:111–131, 1999. [2]
8. (en) D. A. Holton et B. D. McKay, « The smallest non-Hamiltonian 3-connected cubic planar graphs have 38 vertices », Journal of Combinatorial Theory, Series B, vol. 45, n^o 3,‎ 1988, p. 305–319 (DOI 10.1016/0095-8956(88)90075-5)