David Slepian

David Slepian
Biographie
Naissance
Décès
Voir et modifier les données sur Wikidata (à 84 ans)
Nationalité
Formation
Activités
Père
Autres informations
A travaillé pour
Membre de
Conflit
Distinctions

modifier - modifier le code - modifier WikidataDocumentation du modèle

David S. Slepian ( - ) est un mathématicien américain. Il est surtout connu pour ses travaux sur la théorie des codes, la théorie des probabilités et le codage de source distribué. Il est collègue de Claude Shannon et Richard Hamming aux Bell Labs.

Biographie

Né à Pittsburgh, Pennsylvanie, il obtient un B.Sc. à l'Université du Michigan avant de rejoindre l'armée américaine pendant la Seconde Guerre mondiale, en tant qu'officier de tromperie sonique dans l'armée fantôme. Il obtient son doctorat de l'Université Harvard en 1949, écrivant sa thèse en physique. Après des travaux post-doctoraux à l'Université de Cambridge et à l'Université de la Sorbonne, il travaille au Centre de recherche en mathématiques des Laboratoires Bell, où il est le pionnier des travaux sur la théorie du codage algébrique sur les codes de groupe, publiés pour la première fois dans l'article A Class of Binary Signaling Alphabets. Il travaille avec d'autres géants de la théorie de l'information tels que Claude Shannon et Richard Hamming. Il prouve également la possibilité d'une détection singulière, un résultat peut-être peu intuitif. Il est également connu pour le lemme de Slepian en théorie des probabilités (1962) et pour avoir découvert un résultat fondamental dans le codage de source distribué appelé codage Slepian-Wolf avec Jack Keil Wolf (1973).

Il rejoint ensuite l'Université d'Hawaï. Son père Joseph Slepian, est également scientifique[1]. Sa femme est le célèbre auteur pour enfants Jan Slepian (en).

Slepiens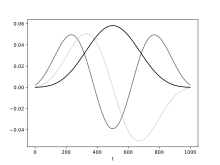

Trois exemples de Slepians, du nom de David Slepian.

Le travail conjoint de Slepian avec HJ Landau et HO Pollak sur les fonctions et séquences d'ondes sphéroïdales prolates discrètes (DPSWF, DPSS) conduit finalement à nommer les séquences comme "Slepians" [2],[3],[4],[5],[6]. La suggestion de dénomination est fournie par Bob Parker de l'Institut océanographique de Scripp, qui suggère que "des séquences sphéroïdales prolates discrètes" étaient une "bouchée".

Ce travail est fondamental pour le développement du multitaper, où la forme discrète est utilisée comme un composant intégral.

Références

  1. ↑ « IEEE Global History Network - David Slepian », IEEE (consulté le )
  2. ↑ « Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty -- I », BSTJ (consulté le )
  3. ↑ « Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty -- II », BSTJ (consulté le )
  4. ↑ « Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty -- III: The Dimension of the Space of Essentially Time- and Band-Limited Signals », BSTJ (consulté le )
  5. ↑ « Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty -- IV: Extensions to Many Dimensions; Generalized Prolate Spheroidal Functions », BSTJ (consulté le )
  6. ↑ « Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty -- V: The Discrete Case », BSTJ (consulté le )

Liens externes