|
Truncamiento (geometría)
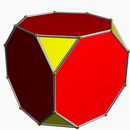
En geometría, un truncamiento es una operación en cualquier dimensión que corta los vértices de un politopo, creando una nueva faceta en el lugar de cada vértice.[1] El término se origina a partir de los nombres de Kepler para los sólidos arquimedianos.[2] Truncamiento uniformeEn general, cualquier poliedro (o politopo) también se puede truncar con un grado de libertad de corte, como se muestra en la operación de truncado de la notación de poliedros de Conway. Un tipo especial de truncamiento, generalmente implícito, es un truncamiento uniforme, un operador de truncamiento aplicado a un poliedro regular (o politopo regular) que produce un poliedro de aristas uniformes (politopo uniforme) con iguales longitudes de arista. No hay grados de libertad, y representa una geometría fija, al igual que los poliedros regulares. En general, todos los politopos uniformes anillados individuales tienen un truncamiento uniforme. Por ejemplo, el icosidodecaedro, representado con los símbolos de Schläfli r{5,3} o , y el diagrama de Coxeter-Dynkin Un truncamiento uniforme realizado en el teselado triangular regular {3,6} da como resultado el teselado hexagonal regular {6,3}. Truncamiento de polígonos
Un polígono de n-lados truncados tendrá 2n caras (aristas). Un polígono regular truncado uniformemente se convertirá en otro polígono regular: t{n} es {2n}. Un truncamiento completo (o rectificación), r{3}, es otro polígono regular en su posición dual.
Un polígono regular también puede representarse por su diagrama de Coxeter-Dynkin, Los polígonos estrellados también pueden ser truncados. Un pentagrama truncado {5/2} se verá como un pentágono, pero en realidad es un decágono de doble cubierta (degenerado) ({10/2}) con dos conjuntos de vértices y aristas superpuestos. Un gran heptagrama truncado {7/3} da un tetradecagrama {14/3}. Truncamiento de poliedros uniformes, teselados regulares y sólidos n-dimensionales Cuando el término se aplica al truncado de sólidos platónicos o teselados regulares, generalmente implica «truncamiento uniforme», lo que significa truncar hasta que las formas originales se conviertan en polígonos regulares. Esta secuencia muestra un ejemplo del truncamiento de un cubo, utilizando los pasos de un proceso continuo de truncamiento entre un cubo lleno y un cubo rectificado. El poliedro final es un cuboctaedro. La imagen del medio es el cubo truncado uniforme. Está representado por un símbolo de Schläfli t{p,q,...}. Un bitruncamiento es un truncamiento más profundo, eliminando todas las aristas originales, pero dejando una parte interior de las caras originales. El octaedro truncado es un cubo bitruncado: 2t{4,3} es un ejemplo. Un bitruncamiento completo, llamada birrectificación, reduce las caras originales a los puntos. Para los poliedros, esto se convierte en el poliedro dual. Un octaedro es una birrectificación del cubo: {3,4} = 2r{4,3} es un ejemplo. Otro tipo de truncamiento, el canteado (también denominado biselado), corta las aristas y los vértices de un poliedro, eliminando las aristas originales y reemplazándolas por rectángulos. Para los politopos de dimensiones más elevadas existen operaciones de truncamientos de grado más alto. La runcinación corta caras, aristas y vértices en figuras de 4 dimensiones, mientras que en 5 dimensiones, una estericación corta celdas, caras, aristas y vértices. Truncamiento de aristasTruncado de los bordes de un cubo, creando un cubo biselado El truncamiento de aristas es un biselado o achaflanado para poliedros, similar al canteado pero que conserva los vértices originales, en el que las aristas se reemplazan por hexágonos. En 4-politopos, el truncamiento de aristas reemplaza las aristas con células en forma de bipirámide elongada. Alternancia o truncamiento parcialUna alternancia uniforme de un cuboctaedro truncado da un cubo romo no uniforme. La alternación o truncamiento parcial elimina solamente algunos de los vértices originales. En truncamiento parcial, o alternancia, la mitad de los vértices y las aristas de conexión se eliminan por completo. La operación se aplica solo a politopos con caras uniformes. Las caras se reducen a la mitad y las caras cuadradas degeneran en aristas. Por ejemplo, el tetraedro es un cubo alterno, h{4,3}. Disminución es un término más general utilizado en el contexto de los sólidos de Johnson para la eliminación de uno o más vértices, aristas o caras de un politopo, sin molestar a los otros vértices. Por ejemplo, el Icosaedro tridisminuido comienza con un icosaedro regular con 3 vértices eliminados. Otros truncamientos parciales están basados en la simetría; por ejemplo, el dodecaedro disminuido tetraédricamente. Truncamientos generalizados El proceso de truncamiento lineal puede generalizarse al permitir truncamientos paramétricos que son negativos, o que van más allá del punto medio de las aristas, causando poliedros de estrellas que se intersecan a sí mismos, y pueden relacionarse con algunos de los polígonos estrellados regulares y poliedros estrellados uniformes.
Véase también
Referencias
Bibliografía
Enlaces externos
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||