es Rombidodecadodecaedro

Mediano hexecontaedro deltoidal
	; Imagen del sólido
Tipo	Poliedro estrellado
Caras	60
Aristas	120
Vértices	54
Grupo de simetría	Ih, [5,3], *532
Poliedro dual	Rombidodecadodecaedro
	[editar datos en Wikidata]

Rombidodecadodecaedro
	; Modelo 3D
Tipo	poliedro estrellado uniforme
Forma de las caras	cuadrado (30); pentagrama (12)
Configuración de vértices	trapecio
Dual	mediano hexecontaedro deltoidal
Elementos
Vértices	60;
Aristas	120;
Caras	54
Más información
MathWorld	Rhombidodecadodecahedron
	[editar datos en Wikidata]

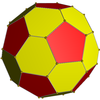
En geometría, el rombidodecadodecaedro es un poliedro uniforme estrellado, indexado como U₃₈. Tiene 54 caras (30 cuadrados, 12 pentágonos y 12 pentagramas), 120 aristas y 60 vértices.^[1] Le corresponde el símbolo de Schläfli t_0,2{⁵⁄₂,5}, y según la construcción de Wythoff también puede ser denominado gran dodecaedro canteado.

Coordenadas cartesianas

Las coordenadas cartesianas de los vértices de un gran rombicosidodecaedro uniforme son todas las permutaciones pares de:

(±1/τ², 0, ±τ²)

(±1, ±1, ±√5)

(±2, ±1/τ, ±τ)

donde τ = (1+√5)/2 es número áureo (a veces escrito φ).

Poliedros relacionados

Comparte su disposición de vértices con el compuesto uniforme de 10 o de 20 prismas triangulares. Además, comparte sus aristas con el icosidodecadodecaedro (que tiene en común las caras pentagonales y pentagrámicas) y con el rombicosaedro (que tiene en común las caras cuadradas).

Envolvente convexa	Rombidodecadodecaedro	Icosidodecadodecaedro
Rombicosaedro	Compuesto de diez prismas triangulares	Compuesto de veinte prismas triangulares

Mediano hexecontaedro deltoidal

El mediano hexecontaedro deltoidal (o mediano ditriacontaedro lanceal) es un poliedro no convexo isoedral. Es el dual del rombidodecadodecaedro, y posee 60 caras cuadriláteras que se cruzan entre sí.

Véase también

Anexo:Poliedros uniformes

Referencias

↑ Maeder, Roman. «38: rhombidodecadodecahedron». MathConsult.

Bibliografía

Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208, doi:10.1017/CBO9780511569371 .

Enlaces externos

Weisstein, Eric W. «Rhombidodecadodecahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Weisstein, Eric W. «Medial deltoidal hexecontahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Poliedros uniformes y duales

Datos: Q29067

[1] Maeder, Roman. «38: rhombidodecadodecahedron». MathConsult.

[1]