Onda inercial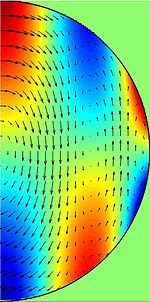

El pulso de onda de inercia ecuatorial causó patrones de flujo de fluido dentro de una cámara esférica de rotación constante. Las flechas en esta sección transversal muestran la dirección y la fuerza del flujo en el plano ecuatorial a medida que la esfera continúa girando hacia la derecha en su eje que se muestra a la izquierda. El rojo indica el flujo fuera del plano; azul indica flujo en el plano.

Las ondas inerciales, también conocidas como oscilaciones inerciales, son un tipo de onda mecánica posible en los fluidos en rotación. A diferencia de las ondas gravitacionales superficiales que se ven comúnmente en la playa o en la bañera, las ondas inerciales fluyen a través del interior del fluido, no hacia la superficie. Como cualquier otro tipo de onda, una onda inercial es causada por una fuerza restauradora y se caracteriza por su longitud de onda y frecuencia. Debido a que la fuerza restauradora de las ondas inerciales es la fuerza de Coriolis, sus longitudes de onda y frecuencias están relacionadas de una manera peculiar. Las ondas inerciales son transversales. Más comúnmente se observan en atmósferas, océanos, lagos y experimentos de laboratorio. Las ondas de Rossby, las corrientes geostróficas y los vientos geostróficos son ejemplos de ondas de inercia. También es probable que existan ondas inerciales en el núcleo fundido de la Tierra en rotación.

Fuerza restauradora

Las ondas inerciales son restauradas al equilibrio por la fuerza de Coriolis, un resultado de la rotación. Para ser precisos, la fuerza de Coriolis surge (junto con la fuerza centrífuga) en un marco giratorio para tener en cuenta el hecho de que dicho marco siempre está acelerando. Las ondas inerciales, por lo tanto, no pueden existir sin rotación. Más complicada que la tensión en una cuerda, la fuerza de Coriolis actúa en un ángulo de 90 ° con respecto a la dirección del movimiento, y su fuerza depende de la velocidad de rotación del fluido. Estas dos propiedades conducen a las características peculiares de las ondas de inercia.

Características

Las ondas inerciales son posibles solo cuando un fluido está girando, y existen en la mayor parte del fluido, no en su superficie. Al igual que las ondas luminosas, las ondas inerciales son transversales, lo que significa que sus vibraciones se producen perpendiculares a la dirección del recorrido de la onda. Una característica geométrica peculiar de las ondas inerciales es que su velocidad de fase, que describe el movimiento de las crestas y valles de la onda, es perpendicular a su velocidad de grupo, que es una medida de la propagación de la energía.

Mientras que una onda de sonido o una onda electromagnética de cualquier frecuencia es posible, las ondas de inercia pueden existir solo en el rango de frecuencias desde cero hasta el doble de la velocidad de rotación del fluido. Además, la frecuencia de la onda está determinada por su dirección de desplazamiento. Las ondas que viajan perpendicularmente al eje de rotación tienen una frecuencia cero y, a veces, se denominan modos geostróficos. Las ondas que viajan paralelas al eje tienen la frecuencia máxima (dos veces la velocidad de rotación), y las ondas en ángulos intermedios tienen frecuencias intermedias. En el espacio libre, una onda inercial puede existir en cualquier frecuencia entre 0 y el doble de la velocidad de rotación. Sin embargo, un contenedor cerrado puede imponer restricciones sobre las posibles frecuencias de las ondas de inercia, como lo puede hacer para cualquier tipo de onda. Las ondas inerciales en un contenedor cerrado a menudo se denominan modos inerciales. En una esfera, por ejemplo, los modos inerciales se ven obligados a tomar frecuencias discretas, dejando espacios donde no pueden existir modos.

Ejemplos de ondas inerciales

Cualquier tipo de fluido puede soportar ondas de inercia: agua, aceite, metales líquidos, aire y otros gases. Las ondas inerciales se observan con mayor frecuencia en atmósferas planetarias (ondas de Rossby, vientos geostróficos) y en océanos y lagos (corrientes geostróficas), donde son responsables de gran parte de la mezcla que tiene lugar.Las olas inerciales afectaron por la pendiente del piso de océano es a menudo llamado Rossby olas. Las ondas de inercia afectadas por la pendiente del fondo del océano a menudo se llaman ondas de Rossby. Las ondas inerciales se pueden observar en experimentos de laboratorio o en flujos industriales donde un fluido está girando.También es probable que existan ondas de inercia en el núcleo externo líquido de la Tierra, y al menos un grupo, como se afirma, evidencia de ellas[1] De manera similar, es probable que las ondas inerciales giren en flujos astronómicos como discos de acreción, anillos planetarios y galaxias.

Descripción matemática

El flujo de fluidos se rige por la ecuación de Navier-Stokes para el momento La velocidad de flujo ${\displaystyle {\vec {u}}}$ de un fluido con viscosidad v bajo presión P y girando a velocidad Ω cambia con el tiempo t de acuerdo a:

${\displaystyle {\frac {\partial {\vec {u}}}{\partial t}}+({\vec {u}}\cdot {\vec {\nabla }}){\vec {u}}=-{\frac {1}{\rho }}{\vec {\nabla }}P+\nu \nabla ^{2}{\vec {u}}-2{\vec {\Omega }}\times {\vec {u}}.}$

El primer término de la derecha explica la presión, el segundo explica la difusión viscosa y el tercer término (el último) en el lado derecho de la ecuación de impulso (arriba) es el término de Coriolis.

Para ser preciso ${\displaystyle {\vec {U}}}$ es la velocidad de flujo como se observa en el marco de referencia giratorio. Como un marco de referencia giratorio se está acelerando (es decir, un marco no inercial), dos fuerzas (pseudo) adicionales (como se mencionó anteriormente) emergen como resultado de esta transformación de coordenadas: la fuerza centrífuga y la fuerza de Coriolis. En la ecuación anterior, ${\displaystyle P}$La fuerza centrífuga se incluye como parte de la presión generalizada P. Es decir, P se relaciona con la presión habitual p dependiendo de la distancia desde el eje de rotación r por${\displaystyle r}$

${\displaystyle P=p+{\frac {1}{2}}\rho r^{2}\Omega ^{2}.}$

En el caso de que la velocidad de rotación sea grande, la fuerza de Coriolis y la fuerza centrífuga se vuelven grandes en comparación con los otros términos. Siendo pequeños en comparación, la difusión y la "derivada convectiva" (segundo término a la izquierda) pueden omitirse. Tomando un rizo de ambos lados y aplicando algunas identidades vectoriales, el resultado es

Una clase de soluciones para esta ecuación son las ondas que satisfacen dos condiciones. Primero, si ${\displaystyle {\vec {K}}}$ es el vector onda

${\displaystyle {\vec {u}}\cdot {\vec {k}}=0,}$

es decir, las ondas deben ser transversales, como se mencionó anteriormente. Segundo, se requiere que las soluciones tengan una frecuencia w que satisfaga la relación de dispersión

${\displaystyle \omega =2{\hat {k}}\cdot {\vec {\Omega }}=2\Omega \cos {\theta },}$

Dónde ${\displaystyle \emptyset }$ Es el ángulo entre el eje de rotación y la dirección de la onda. Estas soluciones particulares son conocidas como ondas inerciales.

La relación de dispersión se parece mucho al término de Coriolis en la ecuación de momento: observe la velocidad de rotación y el factor de dos. Implica inmediatamente el rango de posibles frecuencias para las ondas inerciales, así como la dependencia de su frecuencia en su dirección.

Otras lecturas

• Aldridge, K. D.; I. Lumb (1987). «Inertial waves identified in the Earth's fluid outer core». Nature 325 (6103): 421-423. Bibcode:1987Natur.325..421A. doi:10.1038/325421a0. 
• Greenspan, H. P. (1969). The Theory of Rotating Fluids. Cambridge University Press. 
• Landau, L. D.; E. M. Lifschitz (1987). Fluid Mechanics, Second Edition. New York: Elsevier. ISBN 0-7506-2767-0. 

• Datos: Q1797161