Tobler hyperelliptical projection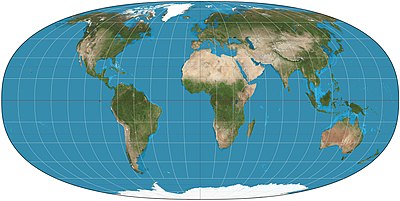

Tobler hyperelliptical projection of the world; α = 0, γ = 1.18314, k = 2.5

The Tobler hyperelliptical projection with Tissot's indicatrix of deformation; α = 0, k = 3

The Tobler hyperelliptical projection is a family of equal-area pseudocylindrical projections that may be used for world maps. Waldo R. Tobler introduced the construction in 1973 as the hyperelliptical projection, now usually known as the Tobler hyperelliptical projection.[1]

Overview

As with any pseudocylindrical projection, in the projection’s normal aspect,[2] the parallels of latitude are parallel, straight lines. Their spacing is calculated to provide the equal-area property. The projection blends the cylindrical equal-area projection, which has straight, vertical meridians, with meridians that follow a particular kind of curve known as superellipses[3] or Lamé curves or sometimes as hyperellipses. A hyperellipse is described by ${\displaystyle x^{k}+y^{k}=\gamma ^{k}}$, where ${\displaystyle \gamma }$ and ${\displaystyle k}$ are free parameters. Tobler's hyperelliptical projection is given as:

${\displaystyle {\begin{aligned}&x=\lambda [\alpha +(1-\alpha ){\frac {(\gamma ^{k}-y^{k})^{1/k}}{\gamma }}]\\\alpha &y=\sin \varphi +{\frac {\alpha -1}{\gamma }}\int _{0}^{y}(\gamma ^{k}-z^{k})^{1/k}dz\end{aligned}}}$

where ${\displaystyle \lambda }$ is the longitude, ${\displaystyle \varphi }$ is the latitude, and ${\displaystyle \alpha }$ is the relative weight given to the cylindrical equal-area projection. For a purely cylindrical equal-area, ${\displaystyle \alpha =1}$; for a projection with pure hyperellipses for meridians, ${\displaystyle \alpha =0}$; and for weighted combinations, ${\displaystyle 0<\alpha <1}$.

When ${\displaystyle \alpha =0}$ and ${\displaystyle k=1}$ the projection degenerates to the Collignon projection; when ${\displaystyle \alpha =0}$, ${\displaystyle k=2}$, and ${\displaystyle \gamma =4/\pi }$ the projection becomes the Mollweide projection.[4] Tobler favored the parameterization shown with the top illustration; that is, ${\displaystyle \alpha =0}$, ${\displaystyle k=2.5}$, and ${\displaystyle \gamma \approx 1.183136}$.

See also

• List of map projections

References

1. Snyder, John P. (1993). Flattening the Earth: 2000 Years of Map Projections. Chicago: University of Chicago Press. p. 220.
2. Mapthematics directory of map projections
3. "Superellipse" in MathWorld encyclopedia
4. Tobler, Waldo (1973). "The hyperelliptical and other new pseudocylindrical equal area map projections". Journal of Geophysical Research. 78 (11): 1753–1759. Bibcode:1973JGR....78.1753T. CiteSeerX 10.1.1.495.6424. doi:10.1029/JB078i011p01753.