|
Bent's rule In chemistry, Bent's rule describes and explains the relationship between the orbital hybridization and the electronegativities of substituents.[1][2] The rule was stated by Henry A. Bent as follows:[2]
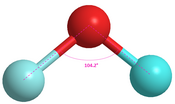
Valence bond theory gives a good approximation of molecular structure. Bent's rule addresses disparities between the observed and idealized geometries.[3] According to Bent's rule, a central atom bonded to multiple groups will rehybridize so that orbitals with more s character are directed towards electropositive groups, and orbitals with more p character will be directed towards groups that are more electronegative. By removing the assumption that all hybrid orbitals are equivalent, Bent's rule leads to improved predictions of molecular geometry and bond strengths.[4][5] Bent's rule can be justified through the relative energy levels of s and p orbitals. Bent's rule represents a modification of VSEPR theory for molecules of lower than ideal symmetry.[6] For bonds with the larger atoms from the lower periods, trends in orbital hybridization depend strongly on both electronegativity and orbital size. HistoryIn the early 1930s, shortly after much of the initial development of quantum mechanics, those theories began to be applied towards molecular structure by Pauling,[7] Slater,[8] Coulson,[9] and others. In particular, Pauling introduced the concept of hybridisation, where atomic s and p orbitals are combined to give hybrid sp, sp2, and sp3 orbitals. Hybrid orbitals proved powerful in explaining the molecular geometries of simple molecules like methane, which is tetrahedral with an sp3 carbon atom and bond angles of 109.5° between the four equivalent C-H bonds. However, slight deviations from these ideal geometries became apparent in the 1940s.[10] A particularly well known example is water, where the angle between the two O-H bonds is only 104.5°. To explain such discrepancies, it was proposed that hybridisation can result in orbitals with unequal s and p character. A. D. Walsh described in 1947[10] a relationship between the electronegativity of groups bonded to carbon and the hybridisation of said carbon atom. Finally, in 1961, Bent published a major review of the literature that related molecular structure, central atom hybridisation, and substituent electronegativities [2] and it is for this work that Bent's rule takes its name. Bent's original paper considers the group electronegativity of the methyl group to be less than that of the hydrogen atom because methyl substitution reduces the acid dissociation constants of formic acid and of acetic acid.[2] Nonbonding orbitalsBent's rule can be extended to rationalize the hybridization of nonbonding orbitals as well. On the one hand, a lone pair (an occupied nonbonding orbital) can be thought of as the limiting case of an electropositive substituent, with electron density completely polarized towards the central atom. Bent's rule predicts that, in order to stabilize the unshared, closely held nonbonding electrons, lone pair orbitals should take on high s character. On the other hand, an unoccupied (empty) nonbonding orbital can be thought of as the limiting case of an electronegative substituent, with electron density completely polarized towards the ligand and away from the central atom. Bent's rule predicts that, in order to leave as much s character as possible for the remaining occupied orbitals, unoccupied nonbonding orbitals should maximize p character. Experimentally, the first conclusion is in line with the reduced bond angles of molecules with lone pairs like water or ammonia compared to methane, while the second conclusion accords with the planar structure of molecules with unoccupied nonbonding orbitals, like monomeric borane and carbenium ions. ConsequencesBent's rule can be used to explain trends in both molecular structure and reactivity. After determining how the hybridisation of the central atom should affect a particular property, the electronegativity of substituents can be examined to see if Bent's rule holds. Bond angles: VSEPR Theory and Bent's RuleValence bond theory predicts that methane is tetrahedral and that ethylene is planar. In water and ammonia, the situation is more complicated because the bond angles are 104.5° and 107° respectively, which are less than the expected tetrahedral angle of 109.5°. One rationale for those deviations is VSEPR theory, where valence electrons are assumed to lie in localized regions and lone pairs are assumed to repel each other to a greater extent than bonding pairs. Bent's rule provides an alternative explanation.  Valence shell electron pair repulsion (VSEPR) theory predicts molecule geometry.[11][12] VSEPR predicts molecular geometry to take the configuration that allows electron pairs to be most spaced out.[11][12] This electron distance maximization happens to achieve the most stable electron distribution.[11][12] The result of VSEPR theory is being able to predict bond angles with accuracy. According to VSEPR theory, the geometry of a molecule can be predicted by counting how many electron pairs and atoms are connected to a central atom.[11][12] Bent's rule states "[A]tomic s character concentrates in orbitals directed toward electropositive substituents".[2] Bent's rule implies that bond angles will deviate from the bond angle predicted by VSEPR theory; the relative electronegativities of atoms surrounding the central atom will impact the molecule geometry.[5] VSEPR theory suggests a way to accurately predict molecule shape using simple rules.[13] However, VSEPR theory predicts observed molecular bond angles only approximately.[13][14] On the other hand, Bent's rule is more accurate.[5] Furthermore, it has been shown that Bent's rule corroborates quantum mechanical computations when describing molecule geometry.[15]
The table above demonstrates the differences between VSEPR theory predicted bond angles and their real-world angles. According to VSEPR theory, diethyl ether, methanol, water and oxygen difluoride should all have a bond angle of 109.5o.[12] Using VSEPR theory, all these molecules should have the same bond angle because they have the same "bent" shape.[12] Yet, clearly the bond angles between all these molecules deviate from their ideal geometries in different ways. Bent's rule can help elucidate these apparent discrepancies.[5][20][21] Electronegative substituents will have more p character.[5][20] Bond angle has a proportional relationship with s character and an inverse relationship with p character.[5] Thus, as substituents become more electronegative, the bond angle of the molecule should decrease. Dimethyl ether, methanol, water and oxygen difluoride follow this trend as expected (as is shown in the table above). Two methyl groups are the substituents attached to the central oxygen in diethyl ether. Because the two methyl groups are electropositive, greater s character will be observed and the real bond angle is larger than the ideal bond angle of 109.5o. Methanol has one electropositive methyl substituent and one electronegative hydrogen substituent. Hence, less s character is observed than dimethyl ether. When there are two hydrogen substituent groups, the angle is decreased even further with the increase in electronegativity and p character. Finally, when both hydrogen substituents are replaced with fluorine in oxygen difluoride, there is another decrease in the bond angle. Fluorine is highly electronegative, resulting in this significant decrease in bond angle. In predicting the bond angle of water, Bent's rule suggests that hybrid orbitals with more s character should be directed towards the lone pairs, while that leaves orbitals with more p character directed towards the hydrogens, resulting in deviation from idealized O(sp3) hybrid orbitals with 25% s character and 75% p character. In the case of water, with its 104.5° HOH angle, the OH bonding orbitals are constructed from O(~sp4.0) orbitals (~20% s, ~80% p), while the lone pairs consist of O(~sp2.3) orbitals (~30% s, ~70% p). As discussed in the justification above, the lone pairs behave as very electropositive substituents and have excess s character. As a result, the bonding electrons have increased p character. This increased p character in those orbitals decreases the bond angle between them to less than the tetrahedral 109.5°. The same logic can be applied to ammonia (107.0° HNH bond angle, with three N(~sp3.4 or 23% s) bonding orbitals and one N(~sp2.1 or 32% s) lone pair), the other canonical example of this phenomenon. The same trend holds for nitrogen containing compounds. Against the expectations of VSEPR theory but consistent with Bent's rule, the bond angles of ammonia (NH3) and nitrogen trifluoride (NF3) are 107° and 102°, respectively. Unlike VSEPR theory, whose theoretical foundations now appear shaky, Bent's rule is still considered to be an important principle in modern treatments of bonding.[5][22] For instance, a modification of this analysis is still viable, even if the lone pairs of H2O are considered to be inequivalent by virtue of their symmetry (i.e., only s, and in-plane px and py oxygen AOs are hybridized to form the two O-H bonding orbitals σO-H and lone pair nO(σ), while pz becomes an inequivalent pure p-character lone pair nO(π)), as in the case of lone pairs emerging from natural bond orbital methods. For a tetrahedral molecule such as difluoromethane with two types of atom bonded to the central atom, the C-F bond to the more electronegative substituent (F) will involve a carbon orbital with less s character than the C-H bond, so that the angle between the C-F bonds is less than the tetrahedral bond angle of 109.5°.[15][23] Trigonal bipyramid molecules have both with axial and equatorial positions. If there are two types of substituents, the more electronegative substituent will prefer the axial position as there are smaller bond angles between axial and electronegative substituents than between two equatorial substituents.[23] Bond lengthsSimilarly to bond angles, the hybridisation of an atom can be related to the lengths of the bonds it forms.[2] As bonding orbitals increase in s character, the σ bond length decreases.
By adding electronegative substituents and changing the hybridisation of the central atoms, bond lengths can be manipulated. If a molecule contains a structure X-A--Y, replacement of the substituent X by a more electronegative atom changes the hybridization of central atom A and shortens the adjacent A--Y bond.
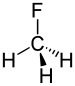
Bonds between elements of disparate electronegativities will be polar and the electron density in such bonds will be shifted towards the more electronegative element. Applying this idea to the molecule fluoromethane illustrates the power of Bent's rule. Because carbon is more electronegative than hydrogen, the electron density in a C-H bond will be shortened and the C-F bond will be elongated. The same trend also holds for the chlorinated analogs of methane, although the effect is less dramatic because chlorine is less electronegative than fluorine.[2]
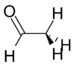
The above cases seem to demonstrate that the size of the chlorine is less important than its electronegativity. A prediction based on sterics alone would lead to the opposite trend, as the large chlorine substituents would be more favorable far apart. As the steric explanation contradicts the experimental result, Bent's rule is likely playing a primary role in structure determination. JCH Coupling constantsPerhaps the most direct measurement of s character in a bonding orbital between hydrogen and carbon is via the 1H−13C coupling constants determined from NMR spectra. Theory predicts that JCH values correlates with s character.[24] In particular, the one bond 13C-1H coupling constant 1J13C-1H is related to the fractional s character of the carbon hybrid orbital used to form the bond through the empirical relationship , where is the s character. (For instance the pure sp3 hybrid atomic orbital found in the C-H bond of methane would have 25% s character resulting in an expected coupling constant of 500 Hz × 0.25 = 125 Hz, in excellent agreement with the experimentally determined value.)
As the electronegativity of the substituent increases, the amount of p character directed towards the substituent increases as well. This leaves more s character in the bonds to the methyl protons, which leads to increased JCH coupling constants. Inductive effectThe inductive effect can be explained with Bent's rule.[25] The inductive effect is the transmission of charge through covalent bonds and Bent's rule provides a mechanism for such results via differences in hybridisation. In the table below,[26] as the groups bonded to the central carbon become more electronegative, the central carbon becomes more electron-withdrawing as measured by the polar substituent constant. The polar substituent constants are similar in principle to σ values from the Hammett equation, as an increasing value corresponds to a greater electron-withdrawing ability. Bent's rule suggests that as the electronegativity of the groups increase, more p character is diverted towards those groups, which leaves more s character in the bond between the central carbon and the R group. As s orbitals have greater electron density closer to the nucleus than p orbitals, the electron density in the C−R bond will more shift towards the carbon as the s character increases. This will make the central carbon more electron-withdrawing to the R group.[10] Thus, the electron-withdrawing ability of the substituents has been transferred to the adjacent carbon, as the inductive effect predicts.
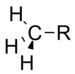
Formal theoryBent's rule provides an additional level of accuracy to valence bond theory. Valence bond theory proposes that covalent bonds consist of two electrons lying in overlapping, usually hybridised, atomic orbitals from two bonding atoms. The assumption that a covalent bond is a linear combination of atomic orbitals of just the two bonding atoms is an approximation (see molecular orbital theory), but valence bond theory is accurate enough that it has had and continues to have a major impact on how bonding is understood.[1] In valence bond theory, two atoms each contribute an atomic orbital and the electrons in the orbital overlap form a covalent bond. Atoms do not usually contribute a pure hydrogen-like orbital to bonds.[7] If atoms could only contribute hydrogen-like orbitals, then the experimentally confirmed tetrahedral structure of methane would not be possible as the 2s and 2p orbitals of carbon do not have that geometry. That and other contradictions led to the proposing of orbital hybridisation. In that framework, atomic orbitals are allowed to mix to produce an equivalent number of orbitals of differing shapes and energies. In the aforementioned case of methane, the 2s and three 2p orbitals of carbon are hybridized to yield four equivalent sp3 orbitals, which resolves the structure discrepancy. Orbital hybridisation allowed valence bond theory to successfully explain the geometry and properties of a vast number of molecules. In traditional hybridisation theory, the hybrid orbitals are all equivalent.[12][27] Namely the atomic s and p orbital(s) are combined to give four spi3 = 1⁄√4(s + √3pi) orbitals, three spi2 = 1⁄√3(s + √2pi) orbitals, or two spi = 1⁄√2(s + pi) orbitals. These combinations are chosen to satisfy two conditions. First, the total amount of s and p orbital contributions must be equivalent before and after hybridisation. Second, the hybrid orbitals must be orthogonal to each other.[27][28] If two hybrid orbitals were not orthogonal, by definition they would have nonzero orbital overlap. Electrons in those orbitals would interact and if one of those orbitals were involved in a covalent bond, the other orbital would also have a nonzero interaction with that bond, violating the two electron per bond tenet of valence bond theory. To construct hybrid s and p orbitals, let the first hybrid orbital be given by s + √λipi, where pi is directed towards a bonding group and λi determines the amount of p character this hybrid orbital has. This is a weighted sum of the wavefunctions. Now choose a second hybrid orbital s + √λjpj, where pj is directed in some way and λj is the amount of p character in this second orbital. The value of λj and direction of pj must be determined so that the resulting orbital can be normalized and so that it is orthogonal to the first hybrid orbital. The hybrid can certainly be normalized, as it is the sum of two normalized wavefunctions. Orthogonality must be established so that the two hybrid orbitals can be involved in separate covalent bonds. The inner product of orthogonal orbitals must be zero and computing the inner product of the constructed hybrids gives the following calculation. The s orbital is normalized and so the inner product ⟨ s | s ⟩ = 1. Also, the s orbital is orthogonal to the pi and pj orbitals, which leads to two terms in the above equaling zero. Finally, the last term is the inner product of two normalized functions that are at an angle of ωij to each other, which gives cos ωij by definition. However, the orthogonality of bonding orbitals demands that 1 + √λiλj cos ωij = 0, so we get Coulson's theorem as a result:[27][29] This means that the four s and p atomic orbitals can be hybridised in arbitrary directions provided that all of the coefficients λ satisfy the above condition pairwise to guarantee the resulting orbitals are orthogonal. Bent's rule, that central atoms direct orbitals of greater p character towards more electronegative substituents, is easily applicable to the above by noting that an increase in the λi coefficient increases the p character of the s + √λipi hybrid orbital. Thus, if a central atom A is bonded to two groups X and Y and Y is more electronegative than X, then A will hybridise so that λX < λY. More sophisticated theoretical and computation techniques beyond Bent's rule are needed to accurately predict molecular geometries from first principles, but Bent's rule provides an excellent heuristic in explaining molecular structures. Henry Bent originally proposed his rule in 1960 on empirical grounds, but a few years later it was supported by molecular orbital calculations by Russell Drago.[23] Applications of Bent's RuleBent's rule is able to characterize molecule geometry with accuracy.[11][5] Bent's rule provides a reliable and robust framework for predicting the bond angles of molecules. Bent's rule accuracy and precision in predicting the geometry of real-world molecules continues to demonstrate its credibility.[5][15] Beyond bond angle prediction, Bent's rule has some significant applications and is of considerable interest to chemists.[11][5][14][21][30] Bent's rule can be applied to analyzing bonding interactions and molecular syntheses. Bent's rule can be used to predict which products are favored in an organic synthesis depending on the starting materials.[14][30] Wang et. al. considered how the substituents affected the silabenzenes' equilibrium and found that Bent's rule played a significant role in the results.[14] The study conducted by Wang et. al. demonstrates how Bent's rule can be used to predict the route of a synthesis and the stability of products.[14] Showing a similar application, Dubois et. al were able to justify some of their findings using Bent's rule when they found a reaction to be irreversible.[30] Both these studies show how Bent's rule can be used to aid synthetic chemistry. Knowing how molecular geometry accurately due to Bent's rule allows synthetic chemists to predict relative product stability.[14][30] Additionally, Bent's rule can help chemists choose their starting materials to drive the reaction towards a particular product.[14] Hence, Bent's rule allows synthetic chemists to exert more control over reactions of interest. See also
References
|






















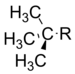



![{\displaystyle {\begin{aligned}\left\langle s+{\sqrt {\lambda _{i}}}p_{i}{\Big \vert }s+{\sqrt {\lambda _{j}}}p_{j}\right\rangle &=\langle s\mid s\rangle +{\sqrt {\lambda _{i}}}\langle s\mid p_{i}\rangle +{\sqrt {\lambda _{j}}}\langle s\mid p_{j}\rangle +{\sqrt {\lambda _{i}\lambda _{j}}}\langle p_{i}\mid p_{j}\rangle \\[4pt]&=1+0+0+{\sqrt {\lambda _{i}\lambda _{j}}}\cos \omega _{ij}=1+{\sqrt {\lambda _{i}\lambda _{j}}}\cos \omega _{ij}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9a0eccf9438e2d82c4e98622999feded965adac)
