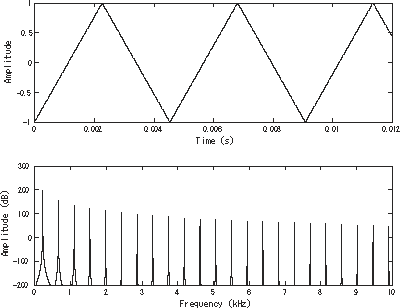
في الصورة موجة مثلثية في المجال الزمني (بالأعلى) وفي مجال التردد (بالأسفل). الموجة الأساسية عند 220 هرتز. نموذج لصوت للموجة المثلثية عند 220 هرتز. إضافة توافقية إلى موجة جيبية لإنتاج موجة مثلثية عند 220 هرتز. الموجة المثلثية (بالإنجليزية Triangle wave) هو موجة غير جيبية ، سميت على اسم شكلها المثلث، وهي موجة دورية ، مستمرة ، حقيقية، خطية متعددة التعريف. مثل الموجة المربعية، تحتوي الموجة المثلثية على عدد فردي من التوافقيات ، حيث إنها دالة فردية ، ومع ذلك، التوافقيات العليا في الموجة المثلثية تكون أسرع بكثير من التوافقيات العليا في الموجة المربعية.[ 1] [ 2]
رسم متحرك لموجة مثلثية مع زيادة عدد التوافقيات، حسب الوصف الرياضي لـ تحويل فورييه . يمكن التعبير عن الموجة المثلثية بواسطة متسلسلة فورييه بالمعادلة التالية، حيث التردد f ، والزمن t :
x
t
r
i
a
n
g
l
e
(
t
)
=
8
π
2
∑
k
=
0
∞
(
−
1
)
k
sin
(
2
π
(
2
k
+
1
)
f
t
)
(
2
k
+
1
)
2
=
8
π
2
(
sin
(
2
π
f
t
)
−
1
9
sin
(
6
π
f
t
)
+
1
25
sin
(
10
π
f
t
)
−
⋯
)
{\displaystyle {\begin{aligned}x_{\mathrm {triangle} }(t)&{}={\frac {8}{\pi ^{2}}}\sum _{k=0}^{\infty }(-1)^{k}\,{\frac {\sin \left(2\pi (2k+1)ft\right)}{(2k+1)^{2}}}\\&{}={\frac {8}{\pi ^{2}}}\left(\sin(2\pi ft)-{1 \over 9}\sin(6\pi ft)+{1 \over 25}\sin(10\pi ft)-\cdots \right)\end{aligned}}}
موجات جيبية ، مربعية ، مثلثية، سن المنشار . تعريف آخر للموجة المثلثية على الفترة من -1 إلى 1، وزمن دوري 2a :
x
(
t
)
=
2
a
(
t
−
a
⌊
t
a
+
1
2
⌋
)
(
−
1
)
⌊
t
a
+
1
2
⌋
{\displaystyle x(t)={\frac {2}{a}}\left(t-a\left\lfloor {\frac {t}{a}}+{\frac {1}{2}}\right\rfloor \right)(-1)^{\left\lfloor {\frac {t}{a}}+{\frac {1}{2}}\right\rfloor }}
حيث الرمز
⌊
n
⌋
{\displaystyle \scriptstyle \lfloor n\rfloor }
دالة السقف للرمز n . أيضًا، يمكن التعبير عن الموجة المثلثية بأنها القيمة المطلقة لموجة سن المنشار:
x
(
t
)
=
|
2
(
t
a
−
⌊
t
a
+
1
2
⌋
)
|
{\displaystyle x(t)=\left|2\left({t \over a}-\left\lfloor {t \over a}+{1 \over 2}\right\rfloor \right)\right|}
وإذا كانت على الفترة من -1 إلى 1:
x
(
t
)
=
2
|
2
(
t
a
−
⌊
t
a
+
1
2
⌋
)
|
−
1
{\displaystyle x(t)=2\left|2\left({t \over a}-\left\lfloor {t \over a}+{1 \over 2}\right\rfloor \right)\right|-1}
كما يمكن التعبير عن الموجة المثلثية بأنها تكامل الموجة المربعية:
∫
sgn
(
sin
(
x
)
)
d
x
{\displaystyle \int \operatorname {sgn}(\sin(x))\,dx\,}
لكي يتم خلق الموجة المثلثية على الأجهزة الإلكترونية بقدرة أقل، نقوم فرض معادلة بسيطة
y
(
0
)
=
1
{\displaystyle y(0)=1}
القيمة المطلقة :
y
(
x
)
=
|
x
mod
4
−
2
|
−
1
{\displaystyle y(x)=|x\,{\bmod {\,}}4-2|-1}
لتعميم المعادلة السابقة، نفرض الزمن الدوري
p
{\displaystyle p}
a
{\displaystyle a}
y
(
0
)
=
a
/
2
{\displaystyle y(0)=a/2}
y
(
x
)
=
2
a
p
(
|
(
x
mod
p
)
−
p
2
|
−
p
4
)
{\displaystyle y(x)={\frac {2a}{p}}{\Biggl (}{\biggl |}\left(x{\bmod {p}}\right)-{\frac {p}{2}}{\biggr |}-{\frac {p}{4}}{\Biggr )}}
بحل (1) و(2)، حيث a=2 ،p=4:
y
(
x
)
=
2
×
2
4
(
|
(
x
mod
4
)
−
4
2
|
−
4
4
)
⇔
{\displaystyle y(x)={\frac {2\times 2}{4}}{\Biggl (}{\biggl |}\left(x{\bmod {4}}\right)-{\frac {4}{2}}{\biggr |}-{\frac {4}{4}}{\Biggr )}\Leftrightarrow }
y
(
x
)
=
(
|
(
x
mod
4
)
−
2
|
−
1
)
{\displaystyle y(x)={\Biggl (}{\biggl |}\left(x{\bmod {4}}\right)-2{\biggr |}-1{\Biggr )}}
لتعديل معادلة (1) تصبح فردية، فقط نقوم بطرح واحد من القيمة المدخلة x، مما يغير طور الدالة الأصلية:
y
(
x
)
=
|
(
x
−
1
)
mod
4
−
2
|
−
1
{\displaystyle y(x)=|(x-1)\,{\bmod {\,}}4-2|-1}
لتعميم معادلة (3) لجعل المعادلة فردبة لأي زمن دوري ومطال :
y
(
x
)
=
4
a
p
(
|
(
(
x
−
p
4
)
mod
p
)
−
p
2
|
−
p
4
)
{\displaystyle y(x)={\frac {4a}{p}}{\Biggl (}{\biggl |}\left((x-{\frac {p}{4}}){\bmod {p}}\right)-{\frac {p}{2}}{\biggr |}-{\frac {p}{4}}{\Biggr )}}
بدلالة دالة الجيب sine و دالة arcsine، حيث "a" تعبر عن المطال، و"p" تعبر عن الزمن الدوري:
y
(
x
)
=
2
a
π
arcsin
(
sin
(
2
π
p
x
)
)
{\displaystyle y(x)={\frac {2a}{\pi }}\arcsin \left(\sin \left({\frac {2\pi }{p}}x\right)\right)}
ملاحظة: sin y = cos x
يمكن التعبير عن طول القوس للموجة المثلثية في زمن دوري "s" بالمعادلة التالية، حيث "a" تعبر عن المطال ، و"p" تعبر عن الزمن الدوري:[ 3]
s
=
(
4
a
)
2
+
p
2
{\displaystyle s={\sqrt {(4a)^{2}+p^{2}}}}