霍夫变换

霍夫變換是一種特徵提取技术，被廣泛應用在圖像分析、電腦視覺以及數位影像處理[1]。 霍夫變換用于辨別找出物件中的特徵，例如：線條。演算法流程大致如下，給定一個物件、要辨別的形狀的種類，演算法會在參數空間（英语：Parameter space）中執行投票來決定物體的形狀，而這是由累加空間（accumulator space）裡的局部最大值來決定。

現在廣泛使用的霍夫變換是由 Richard Duda 和 Peter Hart 在西元1972年發明，並稱之為廣義霍夫變換[2]，廣義霍夫變換和更早前1962年的Paul Hough 的專利有關 [3] [4] 。 經典的霍夫變換是偵測圖片中的直線，之後，霍夫變換不僅能識別直線，也能夠識別任何形狀，常見的有圓形、橢圓形。1981年，因為Dana H. Ballard 的一篇期刊論文 "Generalizing the Hough transform to detect arbitrary shapes"，讓霍夫變換開始流行於计算机視覺界。

歷史

這個變換為了解析氣泡室 (bubble chamber)的圖片才誕生的(Hough, 1959)。

霍夫變換在1962年申請為專利U.S. Patent 3,069,654 （页面存档备份，存于互联网档案馆），其專利名為"辨識複雜圖案的方法及手段"(Method and Means for Recognizing Complex Patterns)。 任一條直線可以由斜率和截距來表示，在該專利中，利用斜率和截距來將一條直線參數化，然而這會導致無界的轉換空間(unbounded transform space)，因為斜率有可能是無限大。

而現在被廣泛使用的${\displaystyle (\rho ,\theta )}$表示式，第一次出現在

Duda, R. O. and P. E. Hart, "Use of the Hough Transformation to Detect Lines and Curves in Pictures," Comm. ACM, Vol. 15, pp. 11–15 (January, 1972),

雖然這早已經是拉東變換的標準。

O'Gorman and Clowes' variation出自

O'Gorman, Frank; Clowes, MB. Finding Picture Edges Through Collinearity of Feature Points. IEEE Trans. Comput. 1976, 25 (4): 449–456. ,

而現代的霍夫變換的發明故事紀載於

Hart, P. E., "How the Hough Transform was Invented" (PDF, 268 kB), IEEE Signal Processing Magazine, Vol 26, Issue 6, pp 18 – 22 (November, 2009).

理論

在自動化分析數位圖片的問題裡，其中一個常有的子問題是偵測某些簡單的直線、圓形、橢圓形。在多數情況下，邊緣偵測器(edge detector)會先用來做圖片前處理，將原本的圖片變成只含有邊緣的圖片。 因為圖片的不完美或是邊緣偵測的不完美，導致有些點(point)或像素(pixel)缺漏，或是有雜訊使得邊緣偵測器所得的邊界偏離了實際的邊界。所以無法直觀的將檢測出的邊緣分成直線、圓形、橢圓形的集合， 而霍夫變換解決了上述問題，藉由霍夫變換演算法中的投票步驟，在複雜的參數空間中找到圖形的參數，電腦可以由參數得知該邊緣(edge)是哪種形狀。

最簡單的霍夫變換是在圖像中識別直線。在平面直角坐標系(x-y)中，一條直線可以用方程式

${\displaystyle y=m_{0}x+b_{0}}$

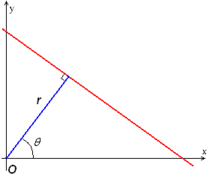
表示，${\displaystyle b_{0}}$是直線的截距，${\displaystyle m_{0}}$是直線的斜率。 而${\displaystyle (m_{0},b_{0})}$可以視為參數空間${\displaystyle (m,b)}$中的一點。當直線垂直於${\displaystyle x}$軸時，斜率為無限大， 若用電腦數值計算時會很不方便，因此Duda 和 Hart [5] 提出使用Hesse normal form來表示直線的參數

${\displaystyle r=x\cos \theta +y\sin \theta }$

${\displaystyle r}$是從原點到直線的距離，${\displaystyle \theta }$是${\displaystyle {\vec {r}}}$和${\displaystyle x}$軸的夾角。利用參數空間${\displaystyle (r,\theta )}$解決了原本參數空間${\displaystyle (m,b)}$發散的問題， 進而能夠比較每一個線段的參數，有人將${\displaystyle (r,\theta )}$平面稱為二維直線的霍夫空間(Hough space)。這個表示方法讓霍夫變換跟二維的拉東變換非常相似，可以說是一體兩面 [6]。

給定一個點${\displaystyle (x_{0},y_{0})}$，通過該點的所有直線的參數${\displaystyle (r,\theta )}$的集合，會在${\displaystyle (r,\theta )}$平面上形成一個三角函數，可由下方程式證明

${\displaystyle r=x_{0}\cos \theta +y_{0}\sin \theta \Rightarrow r={\sqrt {x_{0}^{2}+y_{0}^{2}}}\left({\frac {x_{0}}{\sqrt {x_{0}^{2}+y_{0}^{2}}}}\cos \theta +{\frac {y_{0}}{\sqrt {x_{0}^{2}+y_{0}^{2}}}}\sin \theta \right)\Rightarrow r={\sqrt {x_{0}^{2}+y_{0}^{2}}}\left(\cos \phi \cos \theta +\sin \phi \sin \theta \right)}$

${\displaystyle \Rightarrow r={\sqrt {x_{0}^{2}+y_{0}^{2}}}\cos(\theta -\phi )}$

因此，給定很多點，判斷這些點是否共線的問題，經由霍夫變換之後，變成判斷平面上一堆曲線（每一個點在${\displaystyle (r,\theta )}$平面上代表一條曲線）是否共點（concurrent）的問題。

演算法實作

偵測直線的霍夫變換演算法使用一個稱作累加器(accumulator)二維的矩陣，來偵測圖片中是否有直線可以用方程式${\displaystyle r=x\cos \theta +y\sin \theta }$來描述。 Accumulator矩陣的維度等於未知的參數的總數，舉例來說，要尋找是否有一條直線，他的參數空間的變數總共有兩個${\displaystyle r}$和${\displaystyle \theta }$ ，因此Accumulator矩陣的維度是2。 而這個二維的accumulator矩陣，一個維度代表經過量化(quantized)的${\displaystyle r}$，另一個維度則是代表量化的${\displaystyle \theta }$，因此每一個矩陣的元素(element)的值，是可以用該元素表示的直線 的數量總和，因此矩陣元素的最大值的意義是，該張圖片裡出現該元素代表的直線的信心最大。

對於每一個像素(pixel) ${\displaystyle (x,y)}$與其鄰近的點，演算法會依據一些證據來判斷是否有一條直線通過該像素${\displaystyle (x,y)}$與其鄰近的點，如果有，演算法就會把該條直線的參數 ${\displaystyle (r,\theta )}$所對應到的Accumulator矩陣裡的元素增加1，最後在選出Accumulator矩陣裡，大於阈值(threshold)的一些局部最大值(local maximum)，就可能找到真地存在於圖片上的直線， 在其他狀況下，不使用threshold改用其他的技巧可以讓演算法的表現(performance)更好。然而，霍夫變換只能求得線的參數，無法求得該條線的長度，所以，必須在霍夫變換完的下一步，將線條配對到 圖上的線條。而霍夫變換的誤差來源，可能是圖片的不完美(雜訊、遺漏像素)，使得邊緣偵測器(edge detector)的偵測出錯誤的邊界。

範例

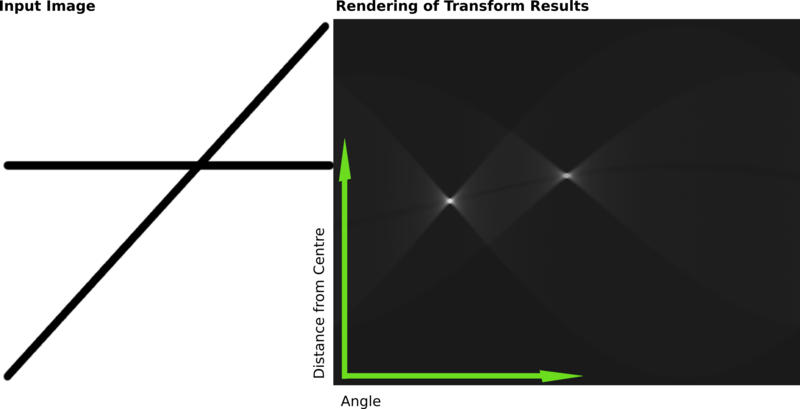
輸入的圖片中有兩條粗直線，經過霍夫變換後的結果得到accumulator矩陣，右圖就是把accumulator矩陣畫出來，越亮值越大，越黑值越小。在右圖中，有兩個很明顯的亮點， 這兩個亮點分別代表兩條不同參數的直線，與輸入的圖片(左圖)吻合。然後讀取矩陣的兩個最大值就可以得出這兩條線距畫面中心距離以及角度。

霍夫變換的變形與延伸

利用梯度的方向(gradient direction)減少投票數

Kernel-based Hough transform (KHT)

限制

霍夫變換透過由投票機制(accumulator矩陣的極大值)來找出線條的參數，這種機制讓霍夫變換能夠在有雜訊的圖片中找出線段。在有雜訊的情況下，如果量化(quantization)的間距(step)太細， 會讓票數分散，換句話說使得應該集中的值分散到極大值附近的矩陣元素[7]。

當參數空間的變數變多，每個矩陣元素的平均大小也會下降，使得正確的參數跟其他參數之間的差變小。另外，每增加一個參數，霍夫變換的複雜度就會增加一個${\displaystyle {\bf {O}}(A^{m-2})}$， ${\displaystyle m}$是參數的總數、${\displaystyle A}$是圖片的大小。因此使用霍夫變換偵測直線和圆以外的形狀時，必須要非常小心上述的問題。

最後，霍夫變換的效率取決於輸入圖片的品質，邊緣必須要正確呈現才能讓霍夫變換有效率，當圖片有雜訊的時候，在霍夫變換的前一級要做抑制雜訊的動作。

注釋

1. Shapiro, Linda and Stockman, George. "Computer Vision", Prentice-Hall, Inc. 2001
2. Duda, R. O. and P. E. Hart, "Use of the Hough Transformation to Detect Lines and Curves in Pictures," Comm. ACM, Vol. 15, pp. 11–15 (January, 1972)
3. Hough, P.V.C. Method and means for recognizing complex patterns, U.S. Patent 3,069,654, Dec. 18, 1962
4. P.V.C. Hough, Machine Analysis of Bubble Chamber Pictures, Proc. Int. Conf. High Energy Accelerators and Instrumentation, 1959
5. Richard O. Duda and Peter E. Hart. Use of the Hough Transformation to Detect Lines and Curves in Pictures (PDF). Artificial Intelligence Center (SRI International). April 1971 [2017-06-30]. （原始内容存档 (PDF)于2012-03-13）. 
6. CiteSeerX — A short introduction to the Radon and Hough transforms and how they relate to each other. [2017-06-30]. （原始内容存档于2012-10-16）. 
7. Image Transforms - Hough Transform. Homepages.inf.ed.ac.uk. [2009-08-17]. （原始内容存档于2021-02-11）. 

參見

• 廣義霍夫變換
• Randomized Hough transform（英语：Randomized Hough transform）
• 拉東變換
• 傅里叶变换