最簡單的類比鎖相迴路 鎖相迴路 (PLL: Phase-locked loops)是利用回授 (Feedback)控制原理实现的频率 及相位 的控制系統 ,其作用是将电路 输出的信號与其外部的参考信號保持同步,当参考信號的频率 或相位 发生改变时,鎖相迴路会检测到这种变化,并且通过其内部的回授 系统来调节输出频率,直到两者重新同步,这种同步又称为“鎖相”(Phase-locked)。
鎖相迴路有許多種,最簡單的鎖相迴路會包括變頻振盪器 鉴相器 ,形成回授 迴路。振盪器產生訊號,鉴相器比較輸出訊號和輸入週期訊號之間的相位,調整振盪器輸出,設法和輸入週期訊號同步。
若讓輸出訊號和輸入訊號之間的相位一致,則兩者的頻率也會一致。因此,鎖相迴路除了讓相位一致之外,也可以追蹤輸入訊號的頻率,或是產生頻率是輸入訊號整數倍的信號。此特性可以用在電腦時脈的同步、解調變 頻率合成
鎖相迴路常用在无线电 、电信 、电子计算机 及其他電子設備中。鎖相迴路也可以用來解調變訊號、從高雜訊的通訊頻道中恢復原始信號、產生頻率為輸入信號頻率整數倍的頻率(頻率合成)、或在數位電路(例如微处理器 )中產生準確的時鐘脈衝。因為單一的積體電路 即可提供完整的鎖相迴路機能,此技術已普遍使用在現在的電子設備中,輸出頻率從1Hz以下,到數GHz。
鎖相迴路可以用賽車來說明:考慮兩部車進行的繞圈賽車,一部車代表輸入信號,另一部車代表鎖相迴路的輸出,也就是壓控振盪器 (VCO)頻率。每一圈代表一個完整的週期。每小時的圈數代表頻率,兩部車之間的距離代表信號之間的相位差。
大部份賽車的過程中,兩部車都可以超過對方或落過對方,這類似鎖相迴路的非鎖相狀態。
但若有事故,賽車場會出現黃色警告旗,此時,任何一部車輛都不允許超過其他的車,也不允許被其他的車超過。此時的兩部車就代表鎖相迴路在鎖相狀態下的輸入信號和輸出信號。每一個駕駛者都會量測其車輛和其他車輛的相位差。若和前車保持的距離太遠了,會設法加速使距離拉近,若和前車保持的距離太近了,會設法減速使距離拉遠。因此,兩部車會保持固定的距離。因為車輛不允許超過其他的車,因此在相同時間內,兩車繞的圈數會相同,因此兩個信號的頻率相同。
相位和時間成正比[ a]
若讓時鐘自行運作,各時鐘計時的速率會有些微的差距。例如牆上的鐘每一小時可能會比國家標準技術研究所 的鐘快了幾秒,隨著時間過去,時間差會越來越大。
若要讓牆上的鐘和參考時鐘同步,可以每一週比較牆上的鐘和參考時鐘的時間(相位比較),然後調整牆上的鐘。若沒有調整,牆上的鐘和參考時鐘的偏差會越來越大。
有些時鐘有計時調整功能,若比較時鐘和標準時鐘,發現時鐘太快了,會設法讓時鐘的計時慢一點,若時鐘太慢了,會設法讓時鐘的計時快一點。若順利的話,時鐘和標準時鐘的誤差會漸漸縮小。幾週後,時鐘就會準確的對應標準時鐘(在時鐘本身的穩定性範圍內,頻率和相位都和標準時鐘一致)。
早期电动机械学 中也有鎖相迴路,例如1921年的Shortt-Synchronome鐘
安森美 HC4046A,是鎖相迴路IC荷兰物理學家克里斯蒂安·惠更斯 早在1673年就發現弱耦合的摆钟 會有自發性同步的情形[ 1] 瑞利男爵 發現弱耦合的風琴管及音叉也有同步的情形[ 2] 威廉·埃克爾斯 [ 3] 爱德华·阿普尔顿 在1923年發現的[ 4]
1925年時,布里斯托尔大学 電機系的大衛·羅賓森(David Robertson)教授,在威尔斯纪念大楼Great George鐘敲鐘出聲的時鐘控制電路中,引入了锁相的概念。羅賓森教授設計的鐘有一個機電裝置可以調整擺鐘的振動速率,所用的修正訊號是來自一個比較電路,在每天上午格林威治時間10點時,比較格林威治天文台的電報脈衝以及擺鐘的相位。其中除了現在電子鎖相迴路中會有的每一個組件之外,羅賓森的設計還有一個特點,其相位比較器是用繼電器邏輯的方式實現相位/頻率比較的機能,一直到1970年代之後才在電子電路中看到類似的設計。羅賓森的研究比後來1932年提出,後來命名為「鎖相迴路」(phase-lock loop)的研究要早。1932年的研究是英國科學家設法想找到可以代替埃德温·霍华德·阿姆斯特朗 的超外差收音机 、同差檢測 直接變換接收機 本機振盪器 [ 5] [ 6] [ 7]
至少從1930年代起,類比電視接收器的鎖相迴路垂直掃描和水平掃描電路,都會和廣播信號的同步信號鎖相[ 8] 西格尼蒂克 在1969年推出了具有完整鎖相迴路機能的單片集成电路 (例如NE565)[ 9] 互補式金屬氧化物半導體 的微功率鎖相迴路IC,是當時廣為使用的積體電路。
一个鎖相迴路电路通常由以下模块构成:
每个模块的简单原理描述如下:
按照实现技术,可以分为模拟鎖相迴路(APLL,Analog PLL)和数字鎖相迴路(DPLL,Digital PLL)。
模拟鎖相迴路(Analog PLL)是指類比的鉴相器,濾波器可能是主動的,也可能是被動的。使用压控振荡器,若其迴路在原點恰有一個極點,則此APLL稱為type II鎖相迴路。
数字鎖相迴路(Digital PLL)是指數位的鉴相器,若濾波器、振盪器也都是數位的(如數控振盪器
按照反馈回路,可以分为整数倍分频鎖相迴路(Integer-N PLL)和分数倍分频鎖相迴路(Fractional-N PLL)。
按照鉴频鉴相器 的实现方式,可以分为電荷泵鎖相迴路 (Charge-Pump PLL)和非电荷泵鎖相迴路。
按照环路的带宽,它可以分为宽带鎖相迴路(Wide band loop PLL)和窄带鎖相迴路(Narrow band loop PLL)。
種類和階數
鎖相迴路頻率範圍 :hold-in範圍(追蹤範圍)、捕獲範圍、鎖定範圍[ 10] 稳定性指标:迴路頻寬,相位裕度 (Phase margin)。
暫態響應:例如過沖、到特定精度(例如50 ppm)的安定時間。
穩態誤差:相位誤差或是時序誤差。
輸出頻譜純淨度:例如特定VCO調諧電壓漣波的邊帶。
相位雜訊:定義為特定頻帶的雜訊能量(例如載波上下10 kHz)。這和VCO相位雜訊、PLL頻寬高度相關。
通用參數:例如能耗、電源範圍、輸出振幅。
鎖相迴路的理想特性是是參考時脈和回授時脈的邊緣可以對正。在PLL已經鎖定時,兩者相位的平均誤差稱為靜態相位偏移(static phase offset)或穩態相位誤差(steady-state phase error)。二個相位之間的變異稱為追隨抖动 。理想上,靜態相位偏移要是0,追隨抖动越小越好[可疑 。
相位雜訊 射極耦合邏輯電路 電晶體-電晶體邏輯 (TTL)或的互補式金屬氧化物半導體 (CMOS)等飽和邏輯特性的零件[ 11]
鎖相迴路的另一個理想特性是在電源及地的電壓突然變化時,其產生的時脈頻率和相位不會受到影響。這稱為電源電壓抑制比 ,抑制比越高越好。
若要改善輸出的相位雜訊,其VCO可以用注入鎖定振盪器
鎖相迴路常用在同步 應用中,例如太空同調解調 位元同步 频率调制 信號的解調變。在無線電發射機中,會用PLL來合成新的頻率,是參考頻率的倍數,和參考頻率有相同的穩定度。
其他的應用有:
频率调制 (FM)訊號的解調變:若PLL鎖定FM訊號,VCO會追蹤輸入信號的瞬時頻率。濾波後的誤差電壓會控制VCO,並且和輸入信號鎖定,這就是解調變後的FM輸出。VCO轉遞特徵會決定解調變輸出的線性度。因為用在PLL積分電路中的VCO是高度線性的信號,因此可以實現高線性度的FM解調變器。頻率偏移調變 (FSK)的解調變:用在數位資料通訊以及電腦週邊上,透過在二個事先設定頻率之間切換的信號來傳輸二進位資料。小信號的恢复(用锁相放大器 來追蹤參考頻率)
恢复資料流(例如來自碟盤存儲 資料)的時脈資訊
微处理器 的倍頻器 调制解调器 的解調變,以及电信 和遙控 訊號的音頻信號。影響信號的数字信号处理 。鎖相迴路也用來同步影片 訊號的相位和頻率,因此可以取樣及進行數位處理。
非接觸式的原子力显微镜 ,偵測探針和表面的交叉作用產生的共振頻率。
直流电动机 电机控制器
有些資料流,特別是高速的串列資料流(例如硬碟磁頭讀到的原始資料流),在傳送時不會將其時脈信號一起送出。接收器利用類似的參考頻率來產生時脈,再利用PLL將其時脈和接收資料的相位鎖定同步。此程序稱為時脈恢復 线路码 (例如8b/10b ),讓二次資料切換時間間隔有一個明確的上限值
[ 12]
若時脈和資料一起傳送,會用時脈為準來進行資料取樣。因為時脈接收後需放大,才能驅動正反器取樣資料。時脈邊緣和接收的資料窗之間會有一個有限大小的時間延遲,長度隨過程、溫度、電壓而不同。此時間延遲會限制傳送資料的速率。有一種消除延遲的方式是在接收端加入一個偏移校正(deskew)的PLL,使得每一次資料正反器的時脈都接收到的時間同相位。此應用中,常會使用一種特殊的鎖相迴路,稱為延遲鎖定迴路 [ 12]
所有的電子系統都會發射一些不想要的無線電訊號。有許多的機構(例如美國的联邦通信委员会 )會限制這些發射的能量,以及其帶來的干擾。發射的雜訊其頻率一般會有一個尖銳的頻譜峰值(一般是在元件的工作頻率,或是其幾倍的諧波)。系統設計者可以用展頻(spread-spectrum)PLL,將頻譜上的能量分散在其他頻段,使峰值降低,以減少對高Q值接收器的干擾。例如,將工作頻率略為往上或往下調整(約1%),工作在數百MHz的元件,可以將其干擾頻譜擴展到數MHz的頻寬範圍內,這可以大幅減少對调频广播 頻道(其頻寬是數萬Hz)的干擾。
一般來說,晶片的參考時脈會驅動晶片中的鎖相迴路(PLL),接著驅動晶片內的時脈分配。時脈分配一般會以平衡分配,設法讓時脈可以同時到達晶片的各個端點。其中一個端點是鎖相迴路的回授輸入。鎖相迴路的功能是比較分配的時脈以及參考時脈,並且調整分配時脈的相位以及頻率,使其分配時脈的相位以及頻率和參考輸入同步。
鎖相迴路無所不在,包括在距離數公尺的系統時鐘校準,也用在晶片中的時脈裡。有時參考信號不一定是單純的時脈信號,也有可能是有夠快資料轉換的資料流,讓鎖相迴路可以從資料流中取得正常且夠快的時脈訊號。有時參考時脈的頻率和分配時脈相同,也有可能分配時脈的頻率和參考頻率之間有有理數的比例關係。
鎖相迴路可以同步的解調變調幅 (AM)信號。鎖相迴路會從調幅信號的載波中還原頻率以及相位資料。VCO收到的相位會和載波差90度,因此會調整相位差使其同步,再送到乘法器中。乘法器的輸出包括頻率信號的和以及差,再經過低通濾波後取得解調變信號。因為PLL只會針對很接近VCO輸出的載波頻率有反應,因此PLL AM偵測器有高度的選擇性以及雜訊抑制能力,這是傳統峰值型解調變器作不到的。不過,若調幅訊號的調變深度到100%,鎖相迴路可能會無法鎖定(lose lock)[ 13]
在數位無線通訊系統(例如GSM、CDMA等)中,在傳輸時會用PLL針對本地振盪器進行上轉換(up-conversion),在接收時也會對本地振盪器進行數位下轉換 頻率合成器 [來源請求]
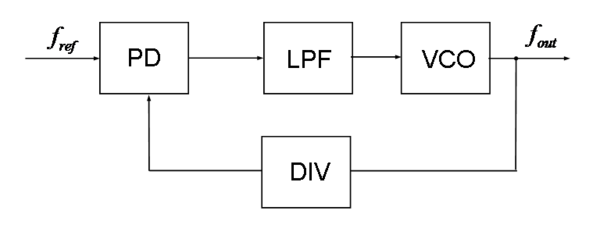
鎖相迴路的方塊圖 鑒相器會比較兩個輸入信號,並產生和其相位差成正比的誤差信號,誤差信號會經過低通濾波,之後驅動壓控振盪器(VCO),以產生輸出相位。此輸出會透過回授迴路(可能再加上除頻器)再成為系統的回授輸入,因此形成负反馈 。若輸出相位偏移,誤差信號會增加,使壓控振盪器的相位往另一個方向變化,以減少相位誤差。因此輸出相位可以鎖定另一輸入信號(稱為參考信號)的相位[來源請求]
類比的鎖相迴路是由類比的鑒相器、低通濾波器以及壓控振盪器組成,形成负反馈的組態。數位的鎖相迴路則會有數位的鑒相器,也可能在參考信號、反馈路徑(或兩者都有)加上除頻器,讓PLL輸出的頻率可以維持為參考信號頻率的有理数 。若將反馈路徑的除以N 除頻器改為可程式化的吞脉冲计数器 ,也可以讓輸出信號的頻率是參考信號的非整數倍。
振盪器會產生週期性的輸出信號。假設一開始振盪器的頻率幾乎和參考信號相同,若振盪器的相位落後參考信號,鑒相器會增加振盪器的控制電壓,使其頻率加快。若振盪器的相位領先參考信號,鑒相器會降低振盪器的控制電壓,使其頻率減慢。因為一開始振盪器的頻率可能會和參考信號的頻率差很多。實務上的鑒相器也會回應頻率差,目的是增加可允許輸入的鎖定範圍。依應用的不同,可能會用壓控振盪器的輸出作為PLL系統的輸出,也可能是以給振盪器的控制信號作為系統輸出[來源請求]
鑒相器(phase detector,簡稱PD)會產生對應二信號相位差的電壓。在鑒相器中,鑒相器的信號輸入分別是參考輸入,以及壓控振盪器(VCO)輸出的回授信號。鑒相器的輸出可以用來控制壓控振盪器,使二信號之間的相位差可以調整為定值,因此整個系統是負回授系統
[ 14]
不同種類的鑒相器有不同的性能特性。
例如,混频器 會產生諧波,因此會產生不希望出現的頻率邊帶,也稱為參考突波(reference spurs),若希望壓控振盪器(VCO)產生的是單一頻率的訊號,這就會增加設計的複雜性。在濾波器設計需求中,會因為這部份的濾波而降低捕獲範圍,或是拉長鎖定時間。在這些應用中會使用比較複雜的數位鑒相器,其輸出不會有嚴重的參考突波問題。而且在鎖波時,其輸入的穩態的相差會接近90度[來源請求]
在鎖相迴路應用中,常需要知道鎖相迴路是否有失鎖(out of lock)的情形,比較複雜的數位鑒相器會有對應失鎖的輸出信號。
數位鎖相迴路中常會使用XOR 门 當作簡易鑒相器。若對線路作一些簡單的修改,也可以用在類比鎖相迴路中。
鎖相迴路濾波器(多半是低通濾波器 )一般會有兩種不同的功能。
第一個功能是決定迴路的動態特性(也稱為穩定性)。這是指迴路對擾動(例如參考頻率的變動、田回授除頻器的變化,或是啟動)的響應特性。常見的考量是迴路可以鎖定的範圍(pull-in範圍、鎖定範圍、捕獲範圍),迴路鎖定的速度(lock時間,lock-up時間或安定時間 )、阻尼 积分 (I,低通濾波器)、导数 (D,高通滤波器 )。迴路的參數常會用波德圖 及相位裕度 進行檢驗。控制理论 中的常用概念(包括PID控制器 )用設計此功能。
第二個功能是限制參考信號的頻率能量範圍(漣波),這是鑒相器輸出以及VCO控制輸入上的信號。此信號上若有不希望出現的頻率邊帶,即為參考突波(reference spurs)。
此模組的設計可能主要會是上述二個功能中的一個,也有可能是比較複雜的模組,設法達到上述二功能。常見的取捨可能是增加系統頻寬,但是會降低穩定值,或是加入阻尼使穩定性變好,但是降低系統反應速度,增加安定時間。上述的調整也會影響相位雜訊。
所有的鎖相迴路都會有可以調整輸出頻率的振盪器,可以是由類比電路驅動的類比振荡器(類比鎖相迴路),或是像部份數位鎖相迴路(DPLL)的作法,使用數位類比轉換器 (D-A converter)。若是全數位鎖相迴路(ADPLL),會用純數位的振荡器[來源請求]
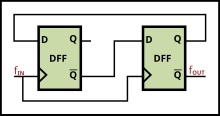
一個數位除頻器(除以4)的例子,可以用在倍數的鎖相迴路 可以在PLL的振盪器和回授輸入之間加入除頻器,以進行頻率合成 石英晶体谐振器 產生許多不同的頻率。
有些PLL在參考時脈和給鑒相器的參考輸入之間加入除頻器。若回授回路有除
N
{\displaystyle N}
M
{\displaystyle M}
N
/
M
{\displaystyle N/M}
乘頻率的PLL也可以用將电子振荡器的輸出鎖定在參考信號的N 次諧波來實現。此時就不用單純的鑒相器,會用諧波混合器(harmonic mixer)。諧波混合器會將參考信號變成有許多諧波的脈衝序列,[ b] N 次諧波和VCO輸出的差異)落在濾波器通帶頻率範圍內。
回授迴路中也不一定只能用除頻器。回授迴路中也可以用乘頻器或頻率混合器。乘頻器會讓VCO的輸出是參考頻率的幾分之一。也可以是這些元件的組合。例如頻率混合器加上除頻器:這可以讓除頻器運作在很低的頻率,但不會影響迴路增益。
用類比乘法器作為鑒相器,使用線性濾波器的類比PLL,可以用以下方式來推導其方程式。令鑒相器的參考輸入為
f
1
(
θ
1
(
t
)
)
{\displaystyle f_{1}(\theta _{1}(t))}
f
2
(
θ
2
(
t
)
)
{\displaystyle f_{2}(\theta _{2}(t))}
θ
1
(
t
)
{\displaystyle \theta _{1}(t)}
θ
2
(
t
)
{\displaystyle \theta _{2}(t)}
f
1
(
θ
)
{\displaystyle f_{1}(\theta )}
f
2
(
θ
)
{\displaystyle f_{2}(\theta )}
波形 的函數。則鑒相器的輸出
φ
(
t
)
{\displaystyle \varphi (t)}
φ
(
t
)
=
f
1
(
θ
1
(
t
)
)
f
2
(
θ
2
(
t
)
)
{\displaystyle \varphi (t)=f_{1}(\theta _{1}(t))f_{2}(\theta _{2}(t))}
VCO頻率會是VCO輸入的函數
g
(
t
)
{\displaystyle g(t)}
θ
˙
2
(
t
)
=
ω
2
(
t
)
=
ω
free
+
g
v
g
(
t
)
{\displaystyle {\dot {\theta }}_{2}(t)=\omega _{2}(t)=\omega _{\text{free}}+g_{v}g(t)\,}
其中
g
v
{\displaystyle g_{v}}
ω
free
{\displaystyle \omega _{\text{free}}}
迴路濾波器可以用以下線性微分方程系統來表示
x
˙
=
A
x
+
b
φ
(
t
)
,
g
(
t
)
=
c
∗
x
,
x
(
0
)
=
x
0
,
{\displaystyle {\begin{array}{rcl}{\dot {x}}&=&Ax+b\varphi (t),\\g(t)&=&c^{*}x,\end{array}}\quad x(0)=x_{0},}
其中
φ
(
t
)
{\displaystyle \varphi (t)}
g
(
t
)
{\displaystyle g(t)}
A
{\displaystyle A}
n
{\displaystyle n}
x
∈
C
n
,
b
∈
R
n
,
c
∈
C
n
,
{\displaystyle x\in \mathbb {C} ^{n},\quad b\in \mathbb {R} ^{n},\quad c\in \mathbb {C} ^{n},\quad }
x
0
∈
C
n
{\displaystyle x_{0}\in \mathbb {C} ^{n}}
共轭转置 。
因此PLL的系統如下
x
˙
=
A
x
+
b
f
1
(
θ
1
(
t
)
)
f
2
(
θ
2
(
t
)
)
,
θ
˙
2
=
ω
free
+
g
v
(
c
∗
x
)
x
(
0
)
=
x
0
,
θ
2
(
0
)
=
θ
0
.
{\displaystyle {\begin{array}{rcl}{\dot {x}}&=&Ax+bf_{1}(\theta _{1}(t))f_{2}(\theta _{2}(t)),\\{\dot {\theta }}_{2}&=&\omega _{\text{free}}+g_{v}(c^{*}x)\\\end{array}}\quad x(0)=x_{0},\quad \theta _{2}(0)=\theta _{0}.}
其中
θ
0
{\displaystyle \theta _{0}}
考慮PLL的參考輸入
f
1
(
θ
1
(
t
)
)
{\displaystyle f_{1}(\theta _{1}(t))}
f
2
(
θ
2
(
t
)
)
{\displaystyle f_{2}(\theta _{2}(t))}
2
π
{\displaystyle 2\pi }
f
1
(
θ
)
{\displaystyle f_{1}(\theta )}
f
2
(
θ
)
{\displaystyle f_{2}(\theta )}
φ
(
θ
)
{\displaystyle \varphi (\theta )}
G
(
t
)
{\displaystyle G(t)}
x
˙
=
A
x
+
b
φ
(
θ
1
(
t
)
−
θ
2
(
t
)
)
,
G
(
t
)
=
c
∗
x
,
x
(
0
)
=
x
0
,
{\displaystyle {\begin{array}{rcl}{\dot {x}}&=&Ax+b\varphi (\theta _{1}(t)-\theta _{2}(t)),\\G(t)&=&c^{*}x,\end{array}}\quad x(0)=x_{0},}
在相位域上漸近等於在時域模型中濾波器的輸出(
G
(
t
)
−
g
(
t
)
{\displaystyle G(t)-g(t)}
[ 15] [ 16]
φ
(
θ
)
{\displaystyle \varphi (\theta )}
鑒相器特性函數 。
相位差標示為
θ
Δ
(
t
)
{\displaystyle \theta _{\Delta }(t)}
θ
Δ
=
θ
1
(
t
)
−
θ
2
(
t
)
.
{\displaystyle \theta _{\Delta }=\theta _{1}(t)-\theta _{2}(t).}
則以下的动力系统 可以描述PLL的行為
x
˙
=
A
x
+
b
φ
(
θ
Δ
)
,
θ
˙
Δ
=
ω
Δ
−
g
v
(
c
∗
x
)
.
x
(
0
)
=
x
0
,
θ
Δ
(
0
)
=
θ
1
(
0
)
−
θ
2
(
0
)
.
{\displaystyle {\begin{array}{rcl}{\dot {x}}&=&Ax+b\varphi (\theta _{\Delta }),\\{\dot {\theta }}_{\Delta }&=&\omega _{\Delta }-g_{v}(c^{*}x).\\\end{array}}\quad x(0)=x_{0},\quad \theta _{\Delta }(0)=\theta _{1}(0)-\theta _{2}(0).}
此處
ω
Δ
=
ω
1
−
ω
free
{\displaystyle \omega _{\Delta }=\omega _{1}-\omega _{\text{free}}}
ω
1
{\displaystyle \omega _{1}}
ω
free
{\displaystyle \omega _{\text{free}}}
考慮弦波信號
f
1
(
θ
1
(
t
)
)
=
A
1
sin
(
θ
1
(
t
)
)
,
f
2
(
θ
2
(
t
)
)
=
A
2
cos
(
θ
2
(
t
)
)
{\displaystyle f_{1}(\theta _{1}(t))=A_{1}\sin(\theta _{1}(t)),\quad f_{2}(\theta _{2}(t))=A_{2}\cos(\theta _{2}(t))}
以及作為濾波器的單極點RC電路 。其時域模型如下
x
˙
=
−
1
R
C
x
+
1
R
C
A
1
A
2
sin
(
θ
1
(
t
)
)
cos
(
θ
2
(
t
)
)
,
θ
˙
2
=
ω
free
+
g
v
(
c
∗
x
)
{\displaystyle {\begin{aligned}{\dot {x}}&=-{\frac {1}{RC}}x+{\frac {1}{RC}}A_{1}A_{2}\sin(\theta _{1}(t))\cos(\theta _{2}(t)),\\[6pt]{\dot {\theta }}_{2}&=\omega _{\text{free}}+g_{v}(c^{*}x)\end{aligned}}}
此信號的鑒相器特性等於[ 17]
φ
(
θ
1
−
θ
2
)
=
A
1
A
2
2
sin
(
θ
1
−
θ
2
)
{\displaystyle \varphi (\theta _{1}-\theta _{2})={\frac {A_{1}A_{2}}{2}}\sin(\theta _{1}-\theta _{2})}
因此相位域模型如下
x
˙
=
−
1
R
C
x
+
1
R
C
A
1
A
2
2
sin
(
θ
Δ
)
,
θ
˙
Δ
=
ω
Δ
−
g
v
(
c
∗
x
)
.
{\displaystyle {\begin{aligned}{\dot {x}}&=-{\frac {1}{RC}}x+{\frac {1}{RC}}{\frac {A_{1}A_{2}}{2}}\sin(\theta _{\Delta }),\\[6pt]{\dot {\theta }}_{\Delta }&=\omega _{\Delta }-g_{v}(c^{*}x).\end{aligned}}}
此系統方程式和單擺的數學方程式等效
x
=
θ
˙
2
−
ω
2
g
v
c
∗
=
ω
1
−
θ
˙
Δ
−
ω
2
g
v
c
∗
,
x
˙
=
θ
¨
2
g
v
c
∗
,
θ
1
=
ω
1
t
+
Ψ
,
θ
Δ
=
θ
1
−
θ
2
,
θ
˙
Δ
=
θ
˙
1
−
θ
˙
2
=
ω
1
−
θ
˙
2
,
1
g
v
c
∗
θ
¨
Δ
−
1
g
v
c
∗
R
C
θ
˙
Δ
−
A
1
A
2
2
R
C
sin
θ
Δ
=
ω
2
−
ω
1
g
v
c
∗
R
C
.
{\displaystyle {\begin{aligned}x&={\frac {{\dot {\theta }}_{2}-\omega _{2}}{g_{v}c^{*}}}={\frac {\omega _{1}-{\dot {\theta }}_{\Delta }-\omega _{2}}{g_{v}c^{*}}},\\[6pt]{\dot {x}}&={\frac {{\ddot {\theta }}_{2}}{g_{v}c^{*}}},\\[6pt]\theta _{1}&=\omega _{1}t+\Psi ,\\[6pt]\theta _{\Delta }&=\theta _{1}-\theta _{2},\\[6pt]{\dot {\theta }}_{\Delta }&={\dot {\theta }}_{1}-{\dot {\theta }}_{2}=\omega _{1}-{\dot {\theta }}_{2},\\[6pt]&{\frac {1}{g_{v}c^{*}}}{\ddot {\theta }}_{\Delta }-{\frac {1}{g_{v}c^{*}RC}}{\dot {\theta }}_{\Delta }-{\frac {A_{1}A_{2}}{2RC}}\sin \theta _{\Delta }={\frac {\omega _{2}-\omega _{1}}{g_{v}c^{*}RC}}.\end{aligned}}}
鎖相迴路也可以進行拉普拉斯变换 ,當做控制系統來分析。其迴路響應可以寫為下式:
θ
o
θ
i
=
K
p
K
v
F
(
s
)
s
+
K
p
K
v
F
(
s
)
{\displaystyle {\frac {\theta _{o}}{\theta _{i}}}={\frac {K_{p}K_{v}F(s)}{s+K_{p}K_{v}F(s)}}}
其中
θ
o
{\displaystyle \theta _{o}}
弧度 。
θ
i
{\displaystyle \theta _{i}}
K
p
{\displaystyle K_{p}}
V /rads
K
v
{\displaystyle K_{v}}
F
(
s
)
{\displaystyle F(s)}
迴路中可以加入不同的迴路濾波器,以控制迴路特性。最簡單的濾波器是一個極點的RC電路 。其迴路傳遞函數如下
F
(
s
)
=
1
1
+
s
R
C
{\displaystyle F(s)={\frac {1}{1+sRC}}}
迴路響應為:
θ
o
θ
i
=
K
p
K
v
R
C
s
2
+
s
R
C
+
K
p
K
v
R
C
{\displaystyle {\frac {\theta _{o}}{\theta _{i}}}={\frac {\frac {K_{p}K_{v}}{RC}}{s^{2}+{\frac {s}{RC}}+{\frac {K_{p}K_{v}}{RC}}}}}
這是標準的諧振子 型式。其分母和以下的二階系統有關:
s
2
+
2
s
ζ
ω
n
+
ω
n
2
{\displaystyle s^{2}+2s\zeta \omega _{n}+\omega _{n}^{2}}
其中
ζ
{\displaystyle \zeta }
阻尼比 ,
ω
n
{\displaystyle \omega _{n}}
自然頻率 。
針對單極點的RC濾波器
ω
n
=
K
p
K
v
R
C
{\displaystyle \omega _{n}={\sqrt {\frac {K_{p}K_{v}}{RC}}}}
ζ
=
1
2
K
p
K
v
R
C
{\displaystyle \zeta ={\frac {1}{2{\sqrt {K_{p}K_{v}RC}}}}}
迴路的自然頻率是量測迴路的響應時間,阻尼比則是和過沖和振鈴(ringing)有關。理想上,自然頻率越高越好,阻尼比應接近0.707(臨界阻尼)。不過針對單極點濾波器,自然頻率和阻尼比兩者無法個別獨立調整。考慮臨界阻尼
R
C
=
1
2
K
p
K
v
{\displaystyle RC={\frac {1}{2K_{p}K_{v}}}}
ω
c
=
K
p
K
v
2
{\displaystyle \omega _{c}=K_{p}K_{v}{\sqrt {2}}}
另外一種比較有效的濾波器,超前-滯後濾波器 (lag-lead filter),其中有一個極點和一個零點,可以用二個電阻和一個電容實現,其傳遞函數為
F
(
s
)
=
1
+
s
C
R
2
1
+
s
C
(
R
1
+
R
2
)
{\displaystyle F(s)={\frac {1+sCR_{2}}{1+sC(R_{1}+R_{2})}}}
此濾波器有二個時間常數
τ
1
=
C
(
R
1
+
R
2
)
{\displaystyle \tau _{1}=C(R_{1}+R_{2})}
τ
2
=
C
R
2
{\displaystyle \tau _{2}=CR_{2}}
自然頻率和阻尼比和時間常數的關係如下
ω
n
=
K
p
K
v
τ
1
{\displaystyle \omega _{n}={\sqrt {\frac {K_{p}K_{v}}{\tau _{1}}}}}
ζ
=
1
2
ω
n
τ
1
+
ω
n
τ
2
2
{\displaystyle \zeta ={\frac {1}{2\omega _{n}\tau _{1}}}+{\frac {\omega _{n}\tau _{2}}{2}}}
因此給定自然頻率和阻尼比,可以針算迴路濾波器的時間常數
τ
1
=
K
p
K
v
ω
n
2
{\displaystyle \tau _{1}={\frac {K_{p}K_{v}}{\omega _{n}^{2}}}}
τ
2
=
2
ζ
ω
n
−
1
K
p
K
v
{\displaystyle \tau _{2}={\frac {2\zeta }{\omega _{n}}}-{\frac {1}{K_{p}K_{v}}}}
真實應用中的迴路濾波器設計會更複雜,可能會使用高階的濾波器去降低特定來源的相位雜訊(可以參考以下D Banerjee的參考資料)。
數位鎖相迴路可以用硬體來實現,例如用像是CMOS 4046的積體電路。不過微處理器的速度越來越快,因此若鎖相的頻率沒有到MHz的等級,這類的應用(例如精準的控制馬達速度)可以用軟體來實現鎖相迴路。用軟體實現數位鎖相迴路有幾個好處,對於反饋迴路的客製比比較簡單(包括參考信號和輸出信號的除頻、倍頻或頻率比例關係)。而且,軟體實現容易瞭解,也容易作實驗。以下是一個用MATLAB實現的數位鉴相器 ,這類的鉴相器強健性高,而且容易實現。
% This example is written in MATLAB
% Initialize variables
vcofreq = zeros ( 1 , numiterations );
ervec = zeros ( 1 , numiterations );
% Keep track of last states of reference, signal, and error signal
qsig = 0 ; qref = 0 ; lref = 0 ; lsig = 0 ; lersig = 0 ;
phs = 0 ;
freq = 0 ;
% Loop filter constants (proportional and derivative)
% Currently powers of two to facilitate multiplication by shifts
prop = 1 / 128 ;
deriv = 64 ;
for it = 1 : numiterations
% Simulate a local oscillator using a 16-bit counter
phs = mod ( phs + floor ( freq / 2 ^ 16 ), 2 ^ 16 );
ref = phs < 32768 ;
% Get the next digital value (0 or 1) of the signal to track
sig = tracksig ( it );
% Implement the phase-frequency detector
rst = ~ ( qsig & qref ); % Reset the "flip-flop" of the phase-frequency
% detector when both signal and reference are high
qsig = ( qsig | ( sig & ~ lsig )) & rst ; % Trigger signal flip-flop and leading edge of signal
qref = ( qref | ( ref & ~ lref )) & rst ; % Trigger reference flip-flop on leading edge of reference
lref = ref ; lsig = sig ; % Store these values for next iteration (for edge detection)
ersig = qref - qsig ; % Compute the error signal (whether frequency should increase or decrease)
% Error signal is given by one or the other flip flop signal
% Implement a pole-zero filter by proportional and derivative input to frequency
filtered_ersig = ersig + ( ersig - lersig ) * deriv ;
% Keep error signal for proportional output
lersig = ersig ;
% Integrate VCO frequency using the error signal
freq = freq - 2 ^ 16 * filtered_ersig * prop ;
% Frequency is tracked as a fixed-point binary fraction
% Store the current VCO frequency
vcofreq ( 1 , it ) = freq / 2 ^ 16 ;
% Store the error signal to show whether signal or reference is higher frequency
ervec ( 1 , it ) = ersig ;
end
在此例子中,假設tracksig 陣列中有要追蹤的參考信號。振盪器是用計數器來實現,計數器的最高位元表示振盪器開啟或是關閉。程式模擬二個D型触发器 ,可以作為相位和頻率的比較器。不論參考信號或回授信號出現上緣時,對應的触发器會為高準位,當二個触发器都是高準位時,會將触发器重置。二個触发器 中何者為高準位,表示參考信號領先回授信號或落後回授信號。誤差信號是這二個触发器值的差值。超前-滯後濾波器是用在濾波誤差信號中入誤差信號以及其導數所得。接下來要進行整合以找到其自然頻率。
在實務上,可以在鎖相迴路的回授中加入其他的動作。例如鎖相迴路是要實現倍頻器,則振盪信號可以先除頻,再和參考信號比較。
^ 若頻率為常數,初始相位為零,弦波的相位就和時間成正比
^ 一般而言,參考弦波會驅動步進恢復二極體
^ Christiaan Huygens, Horologium Oscillatorium … (Paris, France: F. Muguet, 1673), pages 18–19. From page 18: " … illudque accidit memoratu dignum, … brevi tempore reduceret." ( … and it is worth mentioning, since with two clocks constructed in this form and which we suspend in like manner, truly the cross beam is assigned two fulcrums [i.e., two pendulum clocks were suspended from the same wooden beam]; the motions of the pendulums thus share the opposite swings between the two [clocks], since the two clocks at no time move even a small distance, and the sound of both can be heard clearly together always: for if the innermost part [of one of the clocks] is disturbed with a little help, it will have been restored in a short time by the clocks themselves.) English translation provided by Ian Bruce's translation of Horologium Oscillatorium … 页面存档备份 ,存于互联网档案馆 ), pages 16–17.
^ See:
Lord Rayleigh, The Theory of Sound (London, England: Macmillan, 1896), vol. 2. The synchronization of organ pipes in opposed phase is mentioned in §322c, pages 221–222.
Lord Rayleigh (1907) "Acoustical notes — VII," Philosophical Magazine , 6th series, 13 : 316–333. See "Tuning-forks with slight mutual influence," pages 322–323. (页面存档备份 ,存于互联网档案馆 ) ^ See:
Vincent (1919) "On some experiments in which two neighbouring maintained oscillatory circuits affect a resonating circuit," Proceedings of the Physical Society of London , 32 , pt. 2, 84–91.
W. H. Eccles and J. H. Vincent, British Patent Specifications , 163 : 462 (17 Feb. 1920). ^ E. V. Appleton (1923) "The automatic synchronization of triode oscillators," Proceedings of the Cambridge Philosophical Society , 21 (Part III): 231–248. Available on-line at: Internet Archive .
^ Henri de Bellescize, "La réception synchrone," L'Onde Électrique (later: Revue de l'Electricité et de l'Electronique ), vol. 11, pages 230–240 (June 1932).
^ See also: French patent no. 635,451 (filed: 6 October 1931; issued: 29 September 1932); and U.S. patent "Synchronizing system," (页面存档备份 ,存于互联网档案馆 ) no. 1,990,428 (filed: 29 September 1932; issued: 5 February 1935).
^ Notes for a University of Guelph course describing the PLL and early history, including an IC PLL tutorial 互联网档案馆 的存檔 ,存档日期2009-02-24.^ National Television Systems Committee Video Display Signal IO . Sxlist.com. [2010-10-14 ] . (原始内容存档 于2021-02-25). ^ A. B. Grebene, H. R. Camenzind, "Phase Locking As A New Approach For Tuned Integrated Circuits", ISSCC Digest of Technical Papers, pp. 100–101, Feb. 1969.
^ Leonov, G. A.; Kuznetsov, N. V.; Yuldashev, M. V.; Yuldashev, R. V. Hold-in, pull-in, and lock-in ranges of PLL circuits: rigorous mathematical definitions and limitations of classical theory.. IEEE Transactions on Circuits and Systems I: Regular Papers (IEEE). 2015, 62 (10): 2454–2464. S2CID 12292968 arXiv:1505.04262 doi:10.1109/TCSI.2015.2476295 ^ Basab Bijoy Purkayastha; Kandarpa Kumar Sarma. A Digital Phase Locked Loop based Signal and Symbol Recovery System for Wireless Channel. India: Springer (India) Pvt. Ltd. (Part of Springer Scinece+Business Media). 2015: 5. ISBN 978-81-322-2040-4 ^ 12.0 12.1 M Horowitz; C. Yang; S. Sidiropoulos. High-speed electrical signaling: overview and limitations (PDF) . IEEE Micro. 1998-01-01. (原始内容 (PDF) 存档于2006-02-21). ^ Dixon, Robert, Radio Receiver Design, CRC Press: 215, 1998, ISBN 0824701615 ^ Basab Bijoy Purkayastha; Kandarpa Kumar Sarma. A Digital Phase Locked Loop based Signal and Symbol Recovery System for Wireless Channel. India: Springer (India) Pvt. Ltd. (Part of Springer Scinece+Business Media). 2015: 94. ISBN 978-81-322-2040-4 ^ G. A. Leonov, N. V. Kuznetsov, M. V. Yuldashev, R. V. Yuldashev; Kuznetsov; Yuldashev; Yuldashev. Analytical method for computation of phase-detector characteristic (PDF) . IEEE Transactions on Circuits and Systems II: Express Briefs. 2012, 59 (10): 633–637 [2021-05-01 ] . S2CID 2405056 doi:10.1109/TCSII.2012.2213362 存档 (PDF) 于2021-01-20). ^ N.V. Kuznetsov, G.A. Leonov, M.V. Yuldashev, R.V. Yuldashev; Leonov; Yuldashev; Yuldashev. Analytical methods for computation of phase-detector characteristics and PLL design . ISSCS 2011 – International Symposium on Signals, Circuits and Systems, Proceedings. 2011: 7–10 [2021-05-01 ] . ISBN 978-1-61284-944-7S2CID 30208667 doi:10.1109/ISSCS.2011.5978639 存档 于2021-02-26). ^ A. J. Viterbi, Principles of Coherent Communication , McGraw-Hill, New York, 1966
Banerjee, Dean, PLL Performance, Simulation and Design Handbook 4th, National Semiconductor , 2006 [2012-12-04 ] , (原始内容 存档于2012-09-02) Best, R. E., Phase-locked Loops: Design, Simulation and Applications, McGraw-Hill, 2003, ISBN 0-07-141201-8 de Bellescize, Henri, La réception Synchrone, L'Onde Electrique, June 1932, 11 : 230–240 Dorf, Richard C., The Electrical Engineering Handbook, Boca Raton: CRC Press, 1993, Bibcode:1993eeh..book.....D ISBN 0-8493-0185-8 Egan, William F., Phase-Lock Basics, John Wiley & Sons, 1998 Egan, William F., Frequency Synthesis by Phase Lock 2nd, John Wiley and Sons, 2000 Gardner, Floyd M., Phaselock Techniques 3rd, Wiley-Interscience, 2005, ISBN 978-0-471-43063-6 Klapper, J.; Frankle, J. T., Phase-Locked and Frequency-Feedback Systems, Academic Press, 1972 Kundert, Ken, Predicting the Phase Noise and Jitter of PLL-Based Frequency Synthesizers (PDF) 4g, Designer's Guide Consulting, Inc., August 2006 [2008-05-25 ] , (原始内容存档 (PDF) 于2008-05-09) Liu, Mingliang, Build a 1.5-V 2.4-GHz CMOS PLL , Wireless Net Design Line, February 21, 2006, (原始内容 存档于July 1, 2010) Wolaver, Dan H., Phase-Locked Loop Circuit Design, Prentice Hall, 1991, ISBN 0-13-662743-9
D.Banerjee, PLL Performance, Simulation and Design, Fourth Edition, Dog Ear Publishing, LLC, 2006. P.R. Gray et coll., Analysis and Design of Analog Integrated Circuits, Wiley, 2001.
T.H. Lee, The Design of CMOS Radio-Frequency Integrated Circuits, Second Edition, Cambridge University Press, 2003.
B. Razavi, RF Microelectronics, Prentice Hall, 1998.
K. Shu et E. Sánchez-Sinencio, CMOS PLL Synthesizers: Analysis and Design, Springer, 2004.
Predicting the Phase Noise and Jitter of PLL-Based Frequency Synthesizers (页面存档备份 ,存于互联网档案馆 )MIT Open Course: 6.976 High Speed Communication Circuits and Systems, Spring 2003 (页面存档备份 ,存于互联网档案馆 )Circuit sage: Phase Locked Loop Design (页面存档备份 ,存于互联网档案馆 )Dennis Fischette's 1-Stop PLL Center (页面存档备份 ,存于互联网档案馆 )Ask the Applications Engineer - 30 - PLL Synthesizers Jess Chen,“An introduction to the PLL library”, Cadence Design Systems document Agilent EEsof EDA Applications: Phase-Locked Loops (页面存档备份 ,存于互联网档案馆 )PhD thesis: Modeling and simulation techniques for the accurate verification of Integer-N PLLs [永久失效連結





































![{\displaystyle {\begin{aligned}{\dot {x}}&=-{\frac {1}{RC}}x+{\frac {1}{RC}}A_{1}A_{2}\sin(\theta _{1}(t))\cos(\theta _{2}(t)),\\[6pt]{\dot {\theta }}_{2}&=\omega _{\text{free}}+g_{v}(c^{*}x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aa30f8d69878ef11010da5b8a238c9811b425c7)

![{\displaystyle {\begin{aligned}{\dot {x}}&=-{\frac {1}{RC}}x+{\frac {1}{RC}}{\frac {A_{1}A_{2}}{2}}\sin(\theta _{\Delta }),\\[6pt]{\dot {\theta }}_{\Delta }&=\omega _{\Delta }-g_{v}(c^{*}x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a27dc4e09c9f27ca06eda5c20cfd62db61852aa9)
![{\displaystyle {\begin{aligned}x&={\frac {{\dot {\theta }}_{2}-\omega _{2}}{g_{v}c^{*}}}={\frac {\omega _{1}-{\dot {\theta }}_{\Delta }-\omega _{2}}{g_{v}c^{*}}},\\[6pt]{\dot {x}}&={\frac {{\ddot {\theta }}_{2}}{g_{v}c^{*}}},\\[6pt]\theta _{1}&=\omega _{1}t+\Psi ,\\[6pt]\theta _{\Delta }&=\theta _{1}-\theta _{2},\\[6pt]{\dot {\theta }}_{\Delta }&={\dot {\theta }}_{1}-{\dot {\theta }}_{2}=\omega _{1}-{\dot {\theta }}_{2},\\[6pt]&{\frac {1}{g_{v}c^{*}}}{\ddot {\theta }}_{\Delta }-{\frac {1}{g_{v}c^{*}RC}}{\dot {\theta }}_{\Delta }-{\frac {A_{1}A_{2}}{2RC}}\sin \theta _{\Delta }={\frac {\omega _{2}-\omega _{1}}{g_{v}c^{*}RC}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e270e7df2f932355fbcf2a304ac607c0247b75f7)





















