信道 、頻道 或波道 ,是訊號 在通訊系統 中傳輸的通道,由信号从发射端传输到接收端所经过的传输媒质 所構成。广义的信道定义除了包括传输媒质,还包括传输信号的相关设备。
狭义信道,按照传输媒质来划分,可以分为有线信道 、无线信道 和存储信道 三类。
有线信道以导线 为传输媒质,信号沿导线进行传输,信号的能量 集中在导线附近,因此传输效率高,但是部署不够灵活。这一类信道使用的传输媒质包括用电线 传输电信号的架空明线 、电话线 、双绞线 、对称电缆 和同轴电缆 等等,还有传输经过调制 的光脉冲 信号的光导纤维 。
无线信道主要有以辐射无线电波 为传输方式的无线电信道和在水下传播声波的水声信道等。
无线电信号由发射机的天线 辐射 到整个自由空间上进行传播。不同频段 的无线电波有不同的传播方式,主要有:
地波传输 :地球 和电离层 构成波导 ,中长波 、长波 和甚长波 可以在这天然波导 内沿着地面传播并绕过地面的障碍物。长波可以应用于海事通信 ,中波调幅广播 也利用了地波传输。天波传输 :短波 、超短波 可以通过电离层 形成的反射 信道和对流层 形成的散射 信道进行传播。短波电台 就利用了天波传输方式。天波传输的距离最大可以达到400千米左右。电离层和对流层的反射与散射,形成了从发射机到接收机的多条随时间变化的传播路径,电波信号经过这些路径在接收端形成相长或相消的叠加,使得接收信号的幅度和相位呈随机变化,这就是多径信道 的衰落 ,这种信道被称作衰落信道 。视距传输 :对于超短波、微波 等更高频率的电磁波,通常采用直接点对点的直线传输。由于波长很短,无法绕过障碍物,视距传输要求发射机与接收机之间没有物体阻碍。由于地球曲率 的影响,视距传输的距离有限,最远传输距离 d 与发射天线距地面的高度 h 满足
d
=
15
h
km
{\displaystyle d={\sqrt {15h}}\ {\mbox{km}}}
中继站 或卫星 中继站进行接力传输,这就是微波视距中继和卫星中继传输。光信号的视距传输也属于此类。由于电磁波 在水体中传输的损耗很大,在水下通常采用声波的水声信道 进行传输。不同密度 和盐度 的水层形成的反射 、折射 作用和水下物体的散射 作用,使得水声信道也是多径衰落信道。
无线通信 在自由空间(对于无线电信道来说是大气层和太空,对于水声信道来说是水体)上传播信号,因此能量分散、传输效率较低,并且很容易被他人截获,安全性差。但是,无线通信摆脱了对导线的依赖,因此具有有线通信 所没有的高度灵活性。
在某种意义上,磁带 、光盘 、磁盘 等数据存储媒质也可以被看作是一种通信信道。将数据写入存储媒质的过程即等效于发射机将信号传输到信道的过程,将数据从存储媒质读出的过程即等效于接收机从信道接收信号的过程。
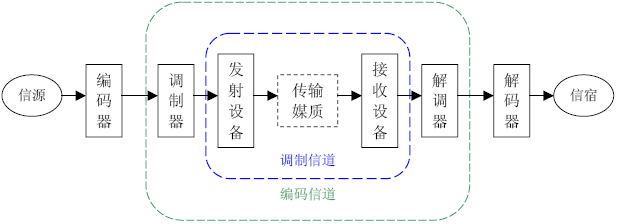
调制信道与编码信道框图。对于数字通信系统,调制信道是编码信道的一部分。 广义信道,按照其功能进行划分,可以分为调制信道 和编码信道 两类。
调制信道是指信号从调制器 的输出端传输到解调器 的输入端经过的部分。对于调制 和解调 的研究者来说,信号在调制信道上经过的传输媒质和变换设备都对信号做出了某种形式的变换 ,研究者只关心这些变换的输入和输出的关系,并不关心实现这一系列变换的具体物理过程。这一系列变换的输入与输出之间的关系,通常用多端口时变网络作为调制信道的数学模型 进行描述。
编码信道是指数字信号由编码器 输出端传输到译码器 输入端经过的部分。对于编译码的研究者来说,编码器输出的数字序列 经过编码信道上的一系列变换之后,在译码器的输入端成为另一组数字序列,研究者只关心这两组数字序列之间的变换关系,而并不关心这一系列变换发生的具体物理过程,甚至并不关心信号在调制信道上的具体变化。编码器输出的数字序列与到译码器输入的数字序列之间的关系,通常用多端口网络的转移概率作为编码信道的数学模型 进行描述。
加性噪声信道模型。由同轴电缆、光纤等媒质构成的信道符合这一模型。 线性时变信道模型。 线性时不变信道模型。 调制信道模型描述的是调制信道的输出信号和输入信号之间的数学关系。调制信道、输入信号、输出信号存在以下特点:
信道总具有输入信号端和输出信号。
信道一般是线性 的,即输入信号和对应的输出信号之间满足叠加原理 。
信道是因果 ,即输入信号经过信道后,相应的输出信号的响应有延时。
信道使通过的信号发生畸变,即输入信号经过信道后,相应的输出信号会发生衰减。
信道中存在雜訊 ,即使输入信号为零,输出信号仍然会具有一定功率 因此,调制信道可以被描述为一个多端口线性系统。如果信号通过信道发生的畸变是时变的,那么这是一个线性时变系统,这样的信道被称作“随机参数信道”;如果畸变与时间无关,那么这是一个线性时不变系统,这种信道被称作“恒定参数信道”。
调制信道的数学模型为:
y
(
t
)
=
x
(
t
)
∗
h
(
t
;
τ
)
+
n
(
t
)
{\displaystyle y(t)=x(t)*h(t;\tau )+n(t)}
其中
x
(
t
)
{\displaystyle x(t)}
y
(
t
)
{\displaystyle y(t)}
h
(
t
;
τ
)
{\displaystyle h(t;\tau )}
冲激响应 ,
τ
{\displaystyle \tau }
h
(
t
;
τ
)
{\displaystyle h(t;\tau )}
τ
{\displaystyle \tau }
δ
(
t
)
{\displaystyle \delta (t)}
卷积 算子。
n
(
t
)
{\displaystyle n(t)}
x
(
t
)
{\displaystyle x(t)}
x
(
t
)
∗
h
(
t
;
τ
)
+
n
(
t
)
{\displaystyle x(t)*h(t;\tau )+n(t)}
x
(
t
)
{\displaystyle x(t)}
h
(
t
;
τ
)
{\displaystyle h(t;\tau )}
x
(
t
)
{\displaystyle x(t)}
y
(
t
)
{\displaystyle y(t)}
矢量 信号。
h
(
t
)
{\displaystyle h(t)}
h
(
t
)
{\displaystyle h(t)}
t
{\displaystyle t}
随机过程 描述其统计 特性,这种信道被称作“随机参数信道”。不过也有信道的乘性干扰基本不随着时间变化,可以认为其
h
(
t
)
{\displaystyle h(t)}
n
(
t
)
{\displaystyle n(t)}
x
{\displaystyle x}
y
{\displaystyle y}
电路 内部的热噪声 和霰彈噪声 ,来自外部的宇宙噪声 等等。
数字通信 将信息通过编码器以数量有限的码元表示。这些码元信号通过编码信道后,由于信道对信号的畸变和噪声干扰,在编码信道输出端由译码器重建的码元信号会发生错误。编码信道模型描述了编码信道的输入码元信号与输出码元信号之间变换的数学关系。
编码信道模型描述了编码信道输入和输出码元信号之间的转移概率 。设编码信道的使用码元集合为
{
c
1
,
c
2
,
…
,
c
M
}
{\displaystyle \{c_{1},c_{2},\ldots ,c_{M}\}}
M
{\displaystyle _{M}}
码本 大小。编码器输出信号为
X
i
,
i
=
1
,
2
,
3
,
…
{\displaystyle X_{i},i=1,2,3,\ldots }
Y
i
,
i
=
1
,
2
,
3
,
…
{\displaystyle Y_{i},i=1,2,3,\ldots }
P
(
Y
j
|
X
i
)
{\displaystyle P(Y_{j}|X_{i})}
X
i
{\displaystyle X_{i}}
Y
j
{\displaystyle Y_{j}}
信道是传输信息的通道,信道容量 描述了信道无差错地传输信息 的最大能力,可以用来衡量信道的好坏。香农 在他的著名论文《通信的数学原理》中给出了信道容量的定义和计算,即信道容量是信道输入信号与输出信号互信息量 的上界。
C
=
sup
p
X
I
(
X
;
Y
)
{\displaystyle C=\sup _{p_{X}}I(X;Y)\,}
对于信噪比 为
S
/
N
{\displaystyle S/N}
带宽 为
B
{\displaystyle B}
C
=
B
log
2
(
1
+
S
/
N
)
{\displaystyle C=B\ \log _{2}(1+S/N)}
log
2
(
1
+
S
/
N
)
{\displaystyle \log _{2}(1+S/N)}
bit
⋅
Hz
−
1
⋅
s
−
1
{\displaystyle {\mbox{bit}}\cdot {\mbox{Hz}}^{-1}\cdot {\mbox{s}}^{-1}}
N
0
{\displaystyle N_{0}}
B
{\displaystyle B}
N
=
B
N
0
{\displaystyle N=BN_{0}}
E
s
{\displaystyle E_{s}}
lim
B
→
∞
B
log
2
(
1
+
E
s
B
N
0
)
≈
1.44
E
s
N
0
{\displaystyle \lim _{B\rightarrow \infty }B\log _{2}\left(1+{\frac {E_{s}}{BN_{0}}}\right)\approx 1.44{\frac {E_{s}}{N_{0}}}}
可见,增加带宽并不是提高信道容量的好方法。
信道容量是理论上信道传输信息的能力的极限,在目前的各种通信技术中,实际能够达到的信道吞吐量 远小于这一极限。
樊昌信:《通信原理》. 北京:国防工业出版社. 2001年
JG Proakis. Digital Communications . McGraw-Hill. 1992
B Sklar. Digital Communications: Fundamentals and Applications . Prentice-Hall. 1988