|
Lý thuyết dầm Euler–Bernoulli Lý thuyết dầm Euler–Bernoulli (còn gọi là lý thuyết dầm kỹ thuật hoặc lý thuyết dầm cổ điển)[1] là lý thuyết đàn hồi tuyến tính được đơn giản hóa để tính toán dầm chịu tải và độ võng (hay lệch) của nó. Lý thuyết bao gồm trường hợp dầm chịu tải trọng phân bố vuông góc với trục và có độ võng nhỏ. Bằng cách bỏ qua sự ảnh hưởng của biến dạng cắt và quán tính quay, lý thuyết dầm Euler–Bernoulli là một trường hợp đặc biệt của lý thuyết dầm Timoshenko mà tính đến biến dạng cắt và cả trường hợp dầm có tiết diện lớn. Lý thuyết dầm cổ điển lần đầu tiên được nêu ra vào năm 1750,[2] nhưng nó không được ứng dụng trên công trình kỹ thuật lớn cho đến khi có kế hoạch xây dựng tháp Eiffel và bánh xe Ferris vào cuối thế kỷ thứ 19. Sau khi những dự án này thành công, lý thuyết này nhanh chóng trở thành nền tảng cho kỹ thuật kết cấu và cơ khí cho phép thúc đẩy cách mạng công nghiệp lần thứ hai. Những công cụ phân tích mở rộng đã được phát triển như lý thuyết tấm và phân tích phần tử hữu hạn, nhưng sự đơn giản của lý thuyết dầm khiến nó trở thành công cụ quan trọng trong kỹ thuật, đặc biệt là cơ học kết cấu và cơ khí. Lịch sử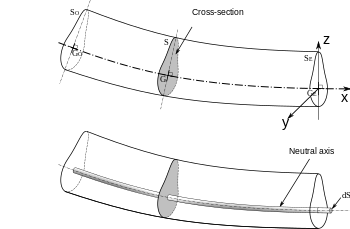 Các nhà lịch sử khoa học đa phần thống nhất rằng Galileo Galilei là người đầu tiên phát triển lý thuyết miêu tả dầm, nhưng cũng có ý kiến cho rằng Leonardo da Vinci là người đầu tiên tiến hành những quan sát quan trọng về tính chất của dầm. Da Vinci không có định luật Hooke và vi tích phân để đi tới lý thuyết hoàn chỉnh, trong khi Galileo lại đưa ra những giả thiết không đúng về cơ sở cho lý thuyết.[3] Dầm Bernoulli đặt tên theo Jacob Bernoulli, ông đã có những khám phá quan trọng liên quan đến đặc tính của dầm. Leonhard Euler và Daniel Bernoulli là những người đầu tiên nêu ra lý thuyết dầm gần đúng vào khoảng 1750.[4] Ở thời điểm đó, khoa học và kỹ thuật được coi là những lĩnh vực khác biệt nhau, và do vậy có những nghi ngờ về các sản phẩm toán học từ những viện hàn lâm có tin cậy để ứng dụng an toàn cho thực tế. Các công trình cầu và tòa nhà vẫn được thiết kế theo những quy tắc cũ cho đến cuối thế kỷ 19, khi tháp Eiffel và bánh xe Ferris đã chứng tỏ sự đúng đắn của lý thuyết cho các công trình và ứng dụng kỹ thuật. Chú thíchTham khảo
|