|
Закон Меткалфа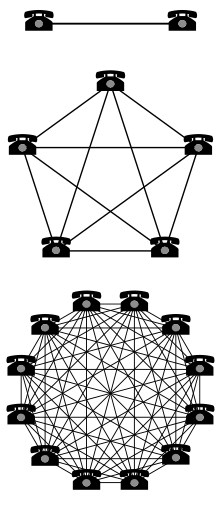 Закон Меткалфа говорить про те, що корисність телекомунікаційної мережі пропорційна квадрату числа підключених до неї користувачів. Вперше сформульований таким чином Джорджем Гілдером у 1993 р.[1], посилаючись на Роберта Меткалфа у відношенні Ethernet, хоч Закон Меткалфа був спочатку представлений у 1980 р., але не на прикладі користувачів, а на підключенні факсів, телефонів.[2] Тільки пізніше, з глобалізацією інтернету, закон дійшов до користувачів і мереж, як спосіб описати підключення до Ethernet.[3] Закон також відноситься до економіки та бізнес менеджменту, особливо до компаній, що змагаються й хочуть об'єднатись з кимось ще. Мережевий впливЗакон Меткалфа характеризується багатьма мережевими впливами на технології комунікації та мережі, такі як Internet, social networking та World Wide Web. Засновник Федеральної Комісії зв'язку США Рід Хандт сказав, що це правило дає розуміння роботи Internet.[4] Закон Меткалфа заснований на факті, що кількість унікальних зв'язків у мережі з кількістю вузлів (n) може бути математично виражено трикутним числом n(n − 1)/2, яке асимптотично наближається до n2. Закон також ілюструвався на прикладі факсів: один факс не ефективний, але користь кожного факсу збільшується залежно від кількості підключених факсів до одної мережі, тому що кількість людей, которим можна відправляти й отримувати документи також росте.[5] ОбмеженняУ доповнення до складності підрахувати «корисність» мережі, математичне підтвердження закону Меткалфа вимірюється тільки потенційною кількістю контактів. Однак суспільна користь мережі залежить від числа вузлів у контакті. Якщо є мовні бар'єри, або інші причини, чому великі частини мережі не з'єднані з іншими частинами, вплив може бути менший. Крім того, Закон Меткалфа передбачає, що корисність кожного вузла n однакова. Наприклад, спочатку був один факс на 50 робітників, потім на половину, на третину, і так далі, поки в кожного не буде факсу. Таким чином, відносна величина додаткового з'єднання зменшується. Також, в соціальних мережах, користувачі, що приєднуються пізніше, використовують мережу менш тих, хто приєднався раніше. Тож користь від кожного додаткового користувача може зменшуватися, роблячи всю мережу менш вигідною, якщо витрати між користувачами фіксовані. Модифіковані моделіУ контексті соціальної мережі, багато хто, в тому числі й Меткалф, пропонував модифікувати моделі, використовуючи (n × log n) пропорційність, ніж n2.[6] Рід й Одлуцко шукали можливі зв'язки з Законом Меткалфа з точки зору зв'язку мережі. Тонга й Вілсон також досліджували відносне питання вартості виключення.[7] Перевірка з фактичними данимиНезважаючи на численні аргументи про закон Меткалфа, не було ніяких даних протягом 30 років вільного доступу, заснованих на доказах за або проти. Тільки в липні 2013 р. голландські дослідники очолювали аналіз Європейського інтернету (активних сторінок) і знайшли (n2) пропорційність для малих значень n та n and (n × log n) для великих значень n.[8] Кілька місяців потому Меткалф самостійно надав ще один доказ, як він використовував данні Facebook за останні 10 років, щоб показати гарний приклад закона Меткалфа (за моделлю n2).[9] Потім, у 2015, Жанг, Луі та Ху продовжили результати Меткалфа, видаляючи данні Tencent (Китайська найбільша соціальна мережа компанії) та Facebook. Їхня робота показала, що закон Меткалфа працює не тільки на Facebook, котрий обслуговує користувачів по всьому світу, а й на Tencent, який обслуговує переважно китайських користувачів. Меткалфівська функція має такий вигляд і відповідно.[10] Дивитись також
Примітки
Додаткова література
|

