Добуток графів

Добуток графів - це бінарна операція на графах. Конкретніше, це операція, яка двом графам G₁ і G₂ ставить у відповідність граф H з такими властивостями:

• Множина вершин графу H - це прямий добуток V(G₁) × V(G₂), де V(G₁) і V(G₂) є множинами вершин G₁ і G₂ відповідно.
• Дві вершини (u_1, u₂) і (v_1, v₂) графу H з'єднані ребром тоді і тільки тоді, коли вершини u_1, u_2, v_1, v₂ задовольняють певним умовам, що відповідають типу добутку (див. нижче).

Види добутків

У таблиці наведено найуживаніші добутки графів. Позначення: ${\displaystyle \sim }$ означає «з'єднані ребром» і ${\displaystyle \not \sim }$ означає «не з'єднані ребром». Символи операцій, наведені нижче, не завжди стандартизовані, особливо в ранніх роботах.

Назва	Умова для (${\displaystyle u_{1}}$, ${\displaystyle u_{2}}$) ∼ (${\displaystyle v_{1}}$, ${\displaystyle v_{2}}$)	Розміри	Приклад
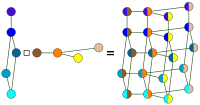
Декартів добуток ${\displaystyle G\square H}$	( ${\displaystyle u_{1}}$ = ${\displaystyle v_{1}}$ і ${\displaystyle u_{2}}$ ${\displaystyle \sim }$ ${\displaystyle v_{2}}$ ) або ( ${\displaystyle u_{1}}$ ${\displaystyle \sim }$ ${\displaystyle v_{1}}$ і ${\displaystyle u_{2}}$ = ${\displaystyle v_{2}}$ )	${\displaystyle G_{V_{1},E_{1}}\square H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1}V_{2})}}$
Тензорний добуток (категорійний добуток) ${\displaystyle G\times H}$	${\displaystyle u_{1}}$ ${\displaystyle \sim }$ ${\displaystyle v_{1}}$ і ${\displaystyle u_{2}}$ ${\displaystyle \sim }$ ${\displaystyle v_{2}}$	${\displaystyle G_{V_{1},E_{1}}\times H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(2E_{1}E_{2})}}$
Лексикографічний добуток ${\displaystyle G\cdot H}$ або ${\displaystyle G[H]}$	u1 ∼ v1 або ( u1 = v1 і u2 ∼ v2 )	${\displaystyle G_{V_{1},E_{1}}\cdot H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1}V_{2}^{2})}}$
Сильний добуток (нормальний добуток) ${\displaystyle G\boxtimes H}$	( u1 = v1 і u2 ∼ v2 ) або ( u1 ∼ v1 і u2 = v2 ) або ( u1 ∼ v1 і u2 ∼ v2 )	${\displaystyle G_{V_{1},E_{1}}\boxtimes H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(V_{1}E_{2}+V_{2}E_{1}+2E_{1}E_{2})}}$
Конормальний добуток (диз'юнктний добуток) ${\displaystyle G*H}$	u1 ∼ v1 або u2 ∼ v2
Модулярний добуток^[en]	${\displaystyle (u_{1}\sim v_{1}}$ і ${\displaystyle u_{2}\sim v_{2})}$ або ${\displaystyle (u_{1}\not \sim v_{1}}$ і ${\displaystyle u_{2}\not \sim v_{2})}$
Кореневий добуток	див. статтю	${\displaystyle G_{V_{1},E_{1}}\cdot H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1})}}$
Добуток Кронекера	див. статтю	див. статтю	див. статтю
Зигзаг-добуток	див. статтю	див. статтю	див. статтю
Замінювальний добуток^[en]
Гомоморфний добуток[1][2] ${\displaystyle G\ltimes H}$	${\displaystyle (u_{1}=v_{1})}$ або ${\displaystyle (u_{1}\sim v_{1}}$ і ${\displaystyle u_{2}\not \sim v_{2})}$

У загальному випадку добуток графів визначається будь-якою умовою для (u_1, u₂) ∼ (v_1, v₂), яку можна виразити в термінах тверджень u₁ ∼ v₁, u₂ ∼ v₂, u₁ = v₁ і u₂ = v₂.

Мнемоніка

Нехай ${\displaystyle K_{2}}$ - повний граф з двома вершинами (тобто одне ребро). Добутки графів ${\displaystyle K_{2}\square K_{2}}$, ${\displaystyle K_{2}\times K_{2}}$, і ${\displaystyle K_{2}\boxtimes K_{2}}$ виглядають так, як знак операції множення. Наприклад, ${\displaystyle K_{2}\square K_{2}}$ є циклом довжини 4 (квадрат), а ${\displaystyle K_{2}\boxtimes K_{2}}$ є повним графом з чотирма вершинами.

Нотація ${\displaystyle G[H]}$ для лексикографічного добутку нагадує, що добуток не комутативний.

Див. також

• Операції над графами

Примітки

1. David E. Roberson, Laura Mancinska. Graph Homomorphisms for Quantum Players. — 2012. — 25 грудня.
2. R. Bačík, S. Mahajan. Computing and Combinatorics. — 1995. — Т. 959. — С. 566, Semidefinite programming and its applications to NP problems. — (Lecture Notes in Computer Science) — ISBN 3-540-60216-X. — DOI:10.1007/BFb0030878.

Література

• Imrich, Wilfried; Klavžar, Sandi. Product Graphs: Structure and Recognition. — Wiley, 2000. — ISBN 0-471-37039-8..