|
Tangentrum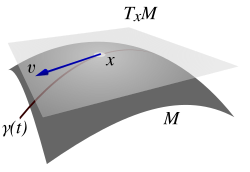 Inom matematiken underlättar tangentrummet till en mångfald generaliseringen av vektorer från affina rymder till allmänna mångfalder, eftersom det i det senare fallet inte är möjligt att med hjälp av två punkter på ett enkelt sätt bilda en vektor som ger förskjutningen mellan punkterna. I differentialgeometrin kan man till varje punkt p i en slät mångfald knyta ett tangentrum som kan betraktas som ett vektorrum som rymmer alla de möjliga riktningar i vilka man kan passera genom p – kallade tangentvektorerna i p. Alla tangentrum har samma dimension som mångfalden. Om mångfalden till exempel är en tvådimensionell sfär kan tangentrummet i en punkt ses som det plan som rätvinkligt mot sfärens radie skär sfären i punkten. Eller, lite mer generellt, håller denna visualisering av tangentrummet om mångfalden är en inbäddad delmångfald av det euklidiska rummet. I algebraisk geometri finns istället en inneboende definition av "tangentrummet i punkten p" som för en varietet V ger ett vektorrum med åtminstone samma dimension som V. De punkter P där vektorrummet har exakt samma dimension som V kallas icke-singulära punkter och alla andra punkter kallas singulära punkter. Om till exempel en kurva korsar sig själv i en punkt saknar kurvan i den punkten en unik tangent. De singulära punkterna är de punkter där "mångfaldstestet" fallerar. Se vidare Zariski-tangentrum. När väl ett tangentrum introducerats kan man definiera vektorfält som abstraktioner av ett hastighetsfält hos partiklar som rör sig på mångfalden. Ett vektorfält är ett slätt (dvs differentierbart) urval som består av en vektor från varje punkts vektorrum. Detta gör att vektorfält kan få definiera en generalisering av en ordinär differentialekvation på en mångfald. Lösningen till en sådan generalisrad differentialekvation är en deriverbar kurva på mångfalden. Derivatan till kurvan i någon punkt ger en tangentvektor i vektorfältet. Dessutom kan man sätta samman en reell mångfalds samtliga tangentrum och bilda en ny, slät mångfald med dubbelt så många dimensioner. En sådan mångfald kallas ett tangentknippe. |