|
Principalkomponentanalys Principalkomponentanalys, ofta förkortat PCA av engelskans principal component analysis, är en linjär ortogonal transform som gör att den transformerade datans dimensioner är ortogonala; det vill säga att de är oberoende och inte har någon kovarians (eller korrelation). PCA introducerades 1901 av Karl Pearson.[1] Alternativa namn är Karhunen–Loève transform (KLT), Hotellingtransform och proper orthogonal decomposition (POD). PCA har likheter med faktoranalys som till skillnad från PCA inte är en ortogonal transform. Typiskt beräknar man PCA på kovariansmatrisen eller korrelationsmatrisen av datan. PCA innebär nu att hitta en linjär transform av data så att kovariansmatrisen blir diagonal, dvs i vilka riktningar data varierar mest. PCA beräknas genom singulärvärdesuppdelning där man beräknar egenvektorerna och dess egenvärden. Egenvektorerna utgör basen för transformerade data, dessa kallas för principalkomponenter eller principalaxlar och utgör de nya dimensionerna; ett nytt koordinatsystem. Detta förfarande kallas även diagonalisering av kovariansmatrisen. Egenvärdena utgör variansen längs med den komponenten. På det här sättet behåller man så mycket som möjligt av variansen i data samtidigt som de nya dimensionerna hålls okorrelerade. Det betyder att den första komponenten representerar den största okorrelerade variansen i data. Det är vanligt att man använder PCA för att reducera antalet dimensioner i data. Eftersom komponenterna är valda efter storlek av oberoende varians antar man att man kan behålla mycket av informationen i data genom att använda enbart de komponenter som representerar en stor del av variansen. Man antar ofta att komponenterna som representerar de lägsta nivåerna av varians utgör brus i data. Genom att använda de första komponenterna och exkludera de övriga kan man representera en stor del av variansen i data. Om man antar att informationen av intresse utgörs av varians är detta ett sätt att reducera antalet dimensioner i data. Denna egenskap kan användas för att lättare hitta samband, kompression, visualisering, utforskande analys av data, eller för att underlätta vidare statistisk analys. ExempelLåt vara en -dimensionell vektor med attribut, till exempel från ett bildigenkänningsproblem. skulle kunna bestå av tre färgvärden för en pixel. Samla exempel på , till exempel från alla pixlar i en given bild. Kovariansmatrisen benämns .   Användning inom genomikInom genetiska associationsstudier använd ofta PCA av flera anledningar. PCA används för att visualisera genetiskt avstånd mellan fall och kontroller i studier för att utesluta population stratifiering, vilket kan leda till falska fynd. Under själva associationsanalysen används ofta punkter uttryckta i ett antal principal komponenter som kovariater för att kompensera för genetisk kopplingsojämvikt. Olinjär PCAGenom att formulera PCA endast uttryckt i skalärprodukter kan man hitta principalkomponenter i rum av mycket högre dimension än ursprungliga data, utan att beräkna vektorerna i detta rum explicit.[2] Figurerna visar ett exempel på detta. Färgerna på punkterna och rutnätet är bara till för att bättre illustrera metoden; de har ingen betydelse för algoritmen. Kärnan som användes var gaussisk, dvs . Kärnan är skalärprodukten av de två vektorerna i R2 av högre dimension.  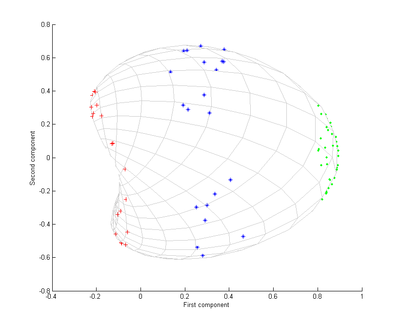 Se ävenReferenser
Externa länkar |




