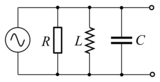
Parallellkoppling

Belysningsslinga		Strömstyrkans fördelning beror av impedanserna

Parallellkoppling är en elektrisk krets där alla komponenter är anslutna till samma spänningsuttag.

Det är vanligt att belysningselement i större lokaler är parallellkopplade. Om ett belysningselement går sönder fortsätter de övriga att lysa.

För en parallellkoppling ligger hela spänningen över var och en av komponenterna medan strömmen fördelas mellan komponenterna i proportion till deras konduktans.

En seriekopplad krets slutar vanligen helt att fungera om en av komponenterna upphör att fungera. För en parallellkopplad krets omfattar funktionsbortfallet endast den felande komponenten.

Parallellkoppling av impedanser

Den strömstyrka som tillförs kretsen är summan av grenströmmarna:

${\displaystyle \ i=i_{1}+i_{2}+...+i_{n}}$

Om U är spänningen över kretsen och z är den impedans som ger samma belastning som de parallella grenarna kan dessa strömmar skrivas som

${\displaystyle {\cfrac {U}{z}}={\cfrac {U}{z_{1}}}+{\cfrac {U}{z_{2}}}+...+{\cfrac {U}{z_{n}}}}$

vilket ger

${\displaystyle {\cfrac {1}{z}}={\cfrac {1}{z_{1}}}+{\cfrac {1}{z_{2}}}+...+{\cfrac {1}{z_{n}}}}$

För två parallella impedanser blir

${\displaystyle \ z={\frac {z_{1}z_{2}}{z_{1}+z_{2}}}}$

För parallellkopplade kondensatorer blir den resulterande kapacitansen

${\displaystyle C=C_{1}+C_{2}+\dots +C_{n}}$

Parallellkopplingsregeln för strömmar

Strömfördelning för parallellkopplade resistorer

En ström I_x genom en resistor R_x, som är parallellkopplad med en grupp av andra resistorer med den resulterande sammanlagda resistansen R_total, kan beräknas som

${\displaystyle I_{x}={\frac {R_{total}}{R_{x}}}I_{total}}$

där I_total är den totala ström som passerar det kombinerade nätverket av R_x parallellkopplad med nätverket av övriga resistorer. Om R_total är sammansatt av parallellkopplade resistorer (till exempel R₁, R₂, ... (inklusive R_x)), måste varje resistors reciproka värde adderas för bestämning av den totala resistansen R_total:

${\displaystyle {\frac {1}{R_{total}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+{\frac {1}{R_{3}}}+...}$

Exempel

Parallellkoppling av resistorer

Givet tre parallella motstånd med resistanserna 1 Ω, 4 Ω och 12 Ω. Ersättningsresistansen R kan bestämmas genom

${\displaystyle {\frac {1}{R}}={\cfrac {1}{1}}+{\cfrac {1}{4}}+{\cfrac {1}{12}}={\frac {16}{12}}={\frac {4}{3}}={\frac {1}{0,75}}}$

Ersättningsresistansen är således 0,75 Ω.

Parallellkoppling av kondensator, induktor och resistor

Impedansens absolutbelopp som funktion av ω (i radianer per sekund) för en parallellkrets med R = 1000Ω, L = 0.1H, C = 1μF.
Resonansfrekvensen ${\displaystyle \omega _{r}={\frac {1}{\sqrt {LC}}}=3162}$ rad/s

Impedansen z för en parallellkoppling av kondensator, induktor och resistor kan beräknas med j-omega-metoden enligt

${\displaystyle {\frac {1}{z}}={\frac {1}{\mathrm {j} \omega L}}+\mathrm {j} \omega C+{\frac {1}{R}}\quad \Rightarrow }$

${\displaystyle z={\frac {\omega LR}{\omega L+\mathrm {j} (\omega ^{2}LC-1)R}}}$

där ${\displaystyle \omega }$ är spänningens frekvens i radianer per sekund.

Resonans

Kretsen befinner sig i resonans när dess impedans är rent resistiv, det vill säga när impedansens imaginärdel är noll, vilket inträffar då

${\displaystyle \omega ^{2}LC-1=0}$

vilket ger resonansfrekvensen som

${\displaystyle \omega _{r}={\frac {1}{\sqrt {LC}}}}$

och impedansen vid resonans som

${\displaystyle z_{r}=R}$

Se även

• Seriekoppling

Externa länkar

• Wikimedia Commons har media som rör Parallellkoppling.
  Bilder & media