Inom matematiken är det n :te harmoniska talet summan av reciprokerna av de n första naturliga talen :
H
n
=
1
+
1
2
+
1
3
+
⋯
+
1
n
=
∑
k
=
1
n
1
k
.
{\displaystyle H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}.}
Harmoniska tal är viktiga inom talteori och är nära relaterade till Riemanns zetafunktion och andra speciella funktioner .
Direkt av harmoniska talens definition följer differensekvationen
H
n
=
H
n
−
1
+
1
n
.
{\displaystyle H_{n}=H_{n-1}+{\frac {1}{n}}.}
Summan av de n första harmoniska talen ges av
∑
k
=
1
n
H
k
=
(
n
+
1
)
H
n
−
n
.
{\displaystyle \sum _{k=1}^{n}H_{k}=(n+1)H_{n}-n.}
Harmoniska talen är relaterade till Stirlingtalen av andra ordningen enligt formeln
H
n
=
1
n
!
[
n
+
1
2
]
.
{\displaystyle H_{n}={\frac {1}{n!}}\left[{n+1 \atop 2}\right].}
En integralrepresentation av Euler är
H
n
=
∫
0
1
1
−
x
n
1
−
x
d
x
.
{\displaystyle H_{n}=\int _{0}^{1}{\frac {1-x^{n}}{1-x}}\,dx.}
Representationen ovan kan bevisas genom att använda identiteten
1
−
x
n
1
−
x
=
1
+
x
+
⋯
+
x
n
−
1
.
{\displaystyle {\frac {1-x^{n}}{1-x}}=1+x+\cdots +x^{n-1}.}
och integrera termvis.
Genom variabelbytet x = 1−u kan man få ett elegant kombinatoriskt uttryck för Hn :
H
n
=
∫
0
1
1
−
x
n
1
−
x
d
x
=
−
∫
1
0
1
−
(
1
−
u
)
n
u
d
u
=
∫
0
1
1
−
(
1
−
u
)
n
u
d
u
=
∫
0
1
[
∑
k
=
1
n
(
−
1
)
k
−
1
(
n
k
)
u
k
−
1
]
d
u
=
∑
k
=
1
n
(
−
1
)
k
−
1
(
n
k
)
∫
0
1
u
k
−
1
d
u
=
∑
k
=
1
n
(
−
1
)
k
−
1
1
k
(
n
k
)
.
{\displaystyle {\begin{aligned}H_{n}&=\int _{0}^{1}{\frac {1-x^{n}}{1-x}}\,dx\\&=-\int _{1}^{0}{\frac {1-(1-u)^{n}}{u}}\,du\\&=\int _{0}^{1}{\frac {1-(1-u)^{n}}{u}}\,du\\&=\int _{0}^{1}\left[\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}u^{k-1}\right]\,du\\&=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}\int _{0}^{1}u^{k-1}\,du\\&=\sum _{k=1}^{n}(-1)^{k-1}{\frac {1}{k}}{\binom {n}{k}}.\end{aligned}}}
Samma representation kan fås genom attanvända den tredje av Retkes identiteter genom att låta
x
1
=
1
,
…
,
x
n
=
n
{\displaystyle x_{1}=1,\ldots ,x_{n}=n}
Π
k
(
1
,
…
,
n
)
=
(
−
1
)
n
−
k
(
k
−
1
)
!
(
n
−
k
)
!
{\displaystyle \Pi _{k}(1,\ldots ,n)=(-1)^{n-k}(k-1)!(n-k)!}
H
n
=
H
n
,
1
=
∑
k
=
1
n
1
k
=
(
−
1
)
n
−
1
n
!
∑
k
=
1
n
1
k
2
Π
k
(
1
,
…
,
n
)
=
∑
k
=
1
n
(
−
1
)
k
−
1
1
k
(
n
k
)
.
{\displaystyle H_{n}=H_{n,1}=\sum _{k=1}^{n}{\frac {1}{k}}=(-1)^{n-1}n!\sum _{k=1}^{n}{\frac {1}{k^{2}\Pi _{k}(1,\ldots ,n)}}=\sum _{k=1}^{n}(-1)^{k-1}{\frac {1}{k}}{\binom {n}{k}}.}
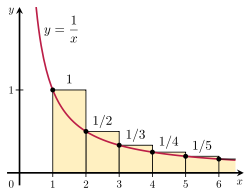
Grafen visar sambandet mellan harmoniska talen och naturliga logaritmen. Det n te harmoniska talet växer ungefär lika snabbt som naturliga logaritmen ur n . Orsanken till detta är att
∫
1
n
1
x
d
x
{\displaystyle \int _{1}^{n}{1 \over x}\,dx}
vars värde är ln(n ).
Värdena av följden H n n ) minskar monotont mot gränsvärdet
lim
n
→
∞
(
H
n
−
ln
n
)
=
γ
,
{\displaystyle \lim _{n\to \infty }\left(H_{n}-\ln n\right)=\gamma ,}
där γ ≈ 0.5772156649 är Eulers konstant . Asymptotiska expansionen då n → ∞ är
H
n
∼
ln
n
+
γ
+
1
2
n
−
∑
k
=
1
∞
B
2
k
2
k
n
2
k
=
ln
n
+
γ
+
1
2
n
−
1
12
n
2
+
1
120
n
4
−
⋯
,
{\displaystyle H_{n}\sim \ln {n}+\gamma +{\frac {1}{2n}}-\sum _{k=1}^{\infty }{\frac {B_{2k}}{2kn^{2k}}}=\ln {n}+\gamma +{\frac {1}{2n}}-{\frac {1}{12n^{2}}}+{\frac {1}{120n^{4}}}-\cdots ,}
där
B
k
{\displaystyle B_{k}}
Bernoullitalen .
Det n -te harmoniska talet kan skrivas som en oändlig serie på följande vis:
1
+
1
2
+
1
3
+
1
4
+
1
5
+
⋯
+
1
n
=
∑
r
=
0
n
−
1
1
n
−
r
=
1
n
∑
r
=
0
n
−
1
n
n
−
r
=
1
n
∑
r
=
0
n
−
1
∑
m
=
0
∞
r
m
n
m
=
1
n
∑
r
=
0
n
−
1
(
1
+
∑
m
=
1
∞
r
m
n
m
)
=
1
+
1
n
∑
r
=
1
n
−
1
∑
m
=
1
∞
r
m
n
m
=
1
+
(
∑
m
=
1
∞
1
n
m
+
1
(
∑
r
=
1
n
−
1
r
m
)
)
=
1
+
1
+
2
+
⋯
+
n
−
1
n
2
+
1
2
+
2
2
+
⋯
+
(
n
−
1
)
2
n
3
+
1
3
+
2
3
+
⋯
+
(
n
−
1
)
3
n
4
+
⋯
{\displaystyle {\begin{aligned}1\,+\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,+\,\cdots \,+\,{\frac {1}{n}}&=\sum _{r=0}^{n-1}{\frac {1}{n-r}}={\frac {1}{n}}\sum _{r=0}^{n-1}{\frac {n}{n-r}}={\frac {1}{n}}\sum _{r=0}^{n-1}\sum _{m=0}^{\infty }{\frac {r^{m}}{n^{m}}}\\&={\frac {1}{n}}\sum _{r=0}^{n-1}\left(1+\sum _{m=1}^{\infty }{\frac {r^{m}}{n^{m}}}\right)\\&=1+{\frac {1}{n}}\sum _{r=1}^{n-1}\sum _{m=1}^{\infty }{\frac {r^{m}}{n^{m}}}\\&=1+\left(\sum _{m=1}^{\infty }{\frac {1}{n^{m+1}}}\left(\sum _{r=1}^{n-1}r^{m}\right)\right)\\&=1+{\frac {1+2+\cdots +n-1}{n^{2}}}+{\frac {1^{2}+2^{2}+\cdots +(n-1)^{2}}{n^{3}}}+{\frac {1^{3}+2^{3}+\cdots +(n-1)^{3}}{n^{4}}}+\cdots \end{aligned}}}
Harmoniska talen förekommer ofta inom talteori och teorin av speciella funktioner såsom i följande formel för digammafunktionen :
ψ
(
n
)
=
H
n
−
1
−
γ
.
{\displaystyle \psi (n)=H_{n-1}-\gamma .}
Denna relation används ofta som definitionen av harmoniska tal för icke-heltal used n . Harmoniska talen används också ofta till att definiera Eulers konstant γ genom gränsvärdet ovan även om
γ
=
lim
n
→
∞
(
H
n
−
ln
(
n
+
1
2
)
)
{\displaystyle \gamma =\lim _{n\to \infty }{\left(H_{n}-\ln \left(n+{1 \over 2}\right)\right)}}
konvergerar snabbare.
2002 bevisade Jeffrey Lagarias att Riemannhypotesen är ekvivalent med att
σ
(
n
)
≤
H
n
+
ln
(
H
n
)
e
H
n
,
{\displaystyle \sigma (n)\leq H_{n}+\ln(H_{n})e^{H_{n}},}
gäller för varje heltal n ≥ 1 med strikt olikhet om n > 1, där σ(n ) är sigmafunktionen .
Egenvärdena av det icke-lokala problemet
λ
ϕ
(
x
)
=
∫
−
1
1
ϕ
(
x
)
−
ϕ
(
y
)
|
x
−
y
|
d
y
{\displaystyle \lambda \phi (x)=\int _{-1}^{1}{\frac {\phi (x)-\phi (y)}{|x-y|}}dy}
ges av
λ
=
2
H
n
{\displaystyle \lambda =2H_{n}}
H
0
=
0.
{\displaystyle H_{0}=0.}
Genererande funktioner
Harmoniska talens genererande funktion är
∑
n
=
1
∞
z
n
H
n
=
−
ln
(
1
−
z
)
1
−
z
,
{\displaystyle \sum _{n=1}^{\infty }z^{n}H_{n}={\frac {-\ln(1-z)}{1-z}},}
En exponentiell genererande funktion ges av
∑
n
=
1
∞
z
n
n
!
H
n
=
−
e
z
∑
k
=
1
∞
1
k
(
−
z
)
k
k
!
=
e
z
Ein
(
z
)
{\displaystyle \sum _{n=1}^{\infty }{\frac {z^{n}}{n!}}H_{n}=-e^{z}\sum _{k=1}^{\infty }{\frac {1}{k}}{\frac {(-z)^{k}}{k!}}=e^{z}{\mbox{Ein}}(z)}
där Ein(z ) är exponentiella integralen . Notera att
Ein
(
z
)
=
E
1
(
z
)
+
γ
+
ln
z
=
Γ
(
0
,
z
)
+
γ
+
ln
z
{\displaystyle {\mbox{Ein}}(z)={\mbox{E}}_{1}(z)+\gamma +\ln z=\Gamma (0,z)+\gamma +\ln z\,}
där Γ(0, z ) är ofullständiga gammafunktionen .
Generaliseringar
Hyperharmoniska tal
J. H. Conway och R. K. Guy har presenterat följande generalisering av harmoniska talen: låt
H
n
(
0
)
=
1
n
.
{\displaystyle H_{n}^{(0)}={\frac {1}{n}}.}
Då är det n te hyperhermoniska talet av ordning r (r>0 )
H
n
(
r
)
=
∑
k
=
1
n
H
k
(
r
−
1
)
.
{\displaystyle H_{n}^{(r)}=\sum _{k=1}^{n}H_{k}^{(r-1)}.}
Speciellt är
H
n
=
H
n
(
1
)
{\displaystyle H_{n}=H_{n}^{(1)}}
Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia , Harmonic number , 19 december 2013 .



![{\displaystyle H_{n}={\frac {1}{n!}}\left[{n+1 \atop 2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51ec1afb6b98d93994321cdc5740d3896519cb3c)


![{\displaystyle {\begin{aligned}H_{n}&=\int _{0}^{1}{\frac {1-x^{n}}{1-x}}\,dx\\&=-\int _{1}^{0}{\frac {1-(1-u)^{n}}{u}}\,du\\&=\int _{0}^{1}{\frac {1-(1-u)^{n}}{u}}\,du\\&=\int _{0}^{1}\left[\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}u^{k-1}\right]\,du\\&=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}\int _{0}^{1}u^{k-1}\,du\\&=\sum _{k=1}^{n}(-1)^{k-1}{\frac {1}{k}}{\binom {n}{k}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c984285566e47364b98a6e2e38e75ecdeb0709e)



















