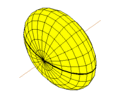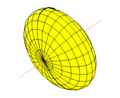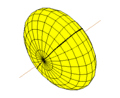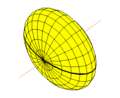
Эллипсоид вращения Эллипсо́ид — поверхность в трёхмерном пространстве , полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей[ 1]
Каноническое уравнение эллипсоида в декартовых координатах , совпадающих с осями деформации эллипсоида:
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
1
,
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1,}
a
,
b
,
c
{\displaystyle a,b,c}
Величины a, b, c называют полуосями эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка .
В случае, когда пара полуосей имеет одинаковую длину, эллипсоид может быть получен вращением эллипса вокруг одной из его осей. Такой эллипсоид называют эллипсоидом вращения сфероидом .
Эллипсоид более точно, чем сфера, отражает идеализированную поверхность Земли .
Параметрическое уравнение эллипсоида:
x
=
a
sin
(
θ
)
cos
(
φ
)
,
y
=
b
sin
(
θ
)
sin
(
φ
)
,
z
=
c
cos
(
θ
)
,
{\displaystyle {\begin{aligned}x&=a\sin(\theta )\cos(\varphi ),\\y&=b\sin(\theta )\sin(\varphi ),\\z&=c\cos(\theta ),\end{aligned}}\,\!}
где
0
≤
θ
≤
π
,
0
≤
φ
<
2
π
.
{\displaystyle 0\leq \theta \leq \pi ,\qquad 0\leq \varphi <2\pi .}
Площадь поверхности эллипсоида вращения[источник не указан 4156 дней :
S
=
4
π
b
2
(
1
+
2
3
e
2
+
3
5
e
4
+
4
7
e
6
+
.
.
.
+
k
+
1
2
k
+
1
e
2
k
+
.
.
.
)
.
{\displaystyle S=4\pi b^{2}\left(1+{\frac {2}{3}}e^{2}+{\frac {3}{5}}e^{4}+{\frac {4}{7}}e^{6}+...+{\frac {k+1}{2k+1}}e^{2k}+...\right).}
В элементарных функциях[источник не указан 4156 дней :
S
o
b
l
a
t
e
=
2
π
a
2
(
1
+
1
−
e
2
e
a
r
t
h
e
)
,
e
2
=
1
−
c
2
a
2
(
c
<
a
)
,
{\displaystyle S_{\rm {oblate}}=2\pi a^{2}\left(1+{\frac {1-e^{2}}{e}}\mathrm {arth} \,e\right)\quad {\mbox{,}}\quad e^{2}=1-{\frac {c^{2}}{a^{2}}}\quad (c<a),}
S
p
r
o
l
a
t
e
=
2
π
a
2
(
1
+
c
a
e
sin
−
1
e
)
,
e
2
=
1
−
a
2
c
2
(
c
>
a
)
,
{\displaystyle S_{\rm {prolate}}=2\pi a^{2}\left(1+{\frac {c}{ae}}\sin ^{-1}e\right)\quad \qquad {\mbox{,}}\;\quad e^{2}=1-{\frac {a^{2}}{c^{2}}}\quad (c>a),}
Oblate, prolate — сплюснутый и вытянутый соответственно.
Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Объём эллипсоида:
V
=
4
3
π
a
b
c
.
{\displaystyle V={\frac {4}{3}}\pi abc.}
Вытянутый эллипсоид вращения
Сплюснутый эллипсоид вращения
Сплюснутый эллипсоид вращения и его образующая
Трехосный эллипсоид с различными длинами полуосей
Ссылки на внешние ресурсы
Словари и энциклопедии