|
Эксперименты Кауфмана — Бухерера — Ноймана Эксперименты Кауфмана — Бухерера — Ноймана измеряли зависимость инерционной массы (или импульса) объекта от его скорости. Историческая важность этой серии экспериментов, проведённых различными физиками между 1901 и 1915 годами, связана с тем, что результаты использовались для проверки предсказаний специальной теории относительности. Развитие точности и анализа данных этих экспериментов и последующее влияние на теоретическую физику в те годы до сих пор являются предметом активных исторических дискуссий, поскольку ранние экспериментальные результаты сначала противоречили только что опубликованной теории Эйнштейна, но более поздние версии этого эксперимента подтвердил её. О современных экспериментах такого рода см. Тесты релятивистской энергии и импульса[англ.], для общей информации см. Экспериментальная проверка специальной теории относительности. Исторический контекстВ 1896 году Анри Беккерель открыл радиоактивный распад ряда химических элементов. Впоследствии было обнаружено, что бета-излучение этих элементов состоит из отрицательно заряженных частиц. Позднее эти частицы были отождествлены с электроном, открытым в экспериментах с катодными лучами Дж. Дж. Томсоном в 1897 г. Интерес был связан с теоретическим предсказанием электромагнитной массы Дж. Дж. Томсоном в 1881 г., который показал, что электромагнитная энергия даёт вклад в массу движущегося заряженного тела[1]. Томсон (1893 г.) и Джордж Фредерик Чарльз Серл (1897 г.) также вычислили, что эта масса зависит от скорости и что она становится бесконечно большой, когда тело движется со скоростью света относительно светоносного эфира[2]. Также Хендрик Лоренц (1899, 1900) предполагал такую зависимость от скорости как следствие своей теории электронов[3]. В это время электромагнитная масса была разделена на «поперечную» и «продольную» массу и иногда обозначалась как «кажущаяся масса», а инвариантная ньютоновская масса обозначалась как «реальная масса»[A 1][A 2]. С другой стороны, немецкий теоретик Макс Абрахам был убежден, что вся масса в конечном итоге окажется электромагнитного происхождения и что ньютоновская механика будет включена в законы электродинамики[A 3]. Понятие (поперечной) электромагнитной массы , основанное на конкретных моделях электрона, позднее превратилось в чисто кинематическое понятие релятивистской массы, касающееся всех форм энергии, а не только электромагнитной энергии. Однако в настоящее время понятие релятивистской массы, хотя оно все ещё часто упоминается в популярных работах по теории относительности, в настоящее время редко используется среди профессиональных работающих физиков и было заменено выражениями для релятивистской энергии и импульса, которые также предсказывают, что скорость света не может быть достигнута массивными телами. Это связано с тем, что эти физические величины включают фактор Лоренца: Таким образом, эксперименты Кауфмана — Бухерера — Ноймана можно рассматривать как ранние проверки релятивистского выражения для энергии и импульса. (Для дальнейшего исторического описания экспериментов по-прежнему используются понятия «поперечная» или «релятивистская масса»). Эксперименты КауфманаПервые эксперименты Вальтер Кауфманн начал экспериментировать с бета-лучами, используя устройство, похожее на электронно-лучевую трубку, где источником электронов были атомы радия, помещённого в вакуумную камеру. (См. рис. 1) Излучение, испускаемое радием, в то время назывались лучами Беккереля. В отличие от известных тогда катодных лучей, которые достигали скорость лишь до 0,3 с, где с — скорость света, лучи Беккереля достигали скорости до 0,9 с. Однако, поскольку бета-частицы имеют разные скорости, излучение было неоднородным. Поэтому Кауфманн прикладывал электрические и магнитные поля, выровненные параллельно друг другу, так что вызванные ими отклонения были перпендикулярны друг другу. Их засветка фотопластинки создавала кривую отклонения, отдельные точки которой соответствовали определённой скорости и определённой массе электронов. Изменяя заряд конденсатора, инвертируя тем самым электрическое поле, можно было получить две симметричные кривые, центральная линия которых определяла направление отклонения траектории в магнитном поле[A 4][A 5]. Кауфман опубликовал первый анализ своих данных в 1901 году, — он действительно смог измерить уменьшение отношения заряда к массе, тем самым продемонстрировав, что масса или импульс увеличиваются со скоростью[4]. Используя формулу Серла (1897 г.) для увеличения электромагнитной энергии заряженных тел со скоростью, он вычислил увеличение электромагнитной массы электрона в зависимости от скорости:
Кауфман заметил, что наблюдаемое увеличение нельзя объяснить этой формулой, поэтому он разделил измеренную общую массу на механическую (истинную) массу и электромагнитную (кажущуюся) массу, причем механическая масса была значительно больше электромагнитной. Однако он допустил две ошибки: как показал Макс Абрахам, Кауфман упустил из виду, что формула Серла применима только в продольном направлении, но для измерения отклонения была важна формула для поперечного направления. Поэтому Абрахам ввёл «поперечную электромагнитную массу» со следующей зависимостью от скорости: Кауфман также допустил расчётную ошибку при выводе кривых прогиба. Эти ошибки были исправлены им в работе 1902 года[5]. В 1902 и 1903 годах Кауфманн провёл ещё одну серию испытаний с обновленными и улучшенными экспериментальными методами. Результаты были интерпретированы им как подтверждение теории Абрахама и предположения, что масса электрона имеет полностью электромагнитное происхождение[6][7]. Герман Штарке провёл аналогичные измерения в 1903 году, хотя он использовал катодные лучи, ограниченные 0,3c. Полученные им результаты были интерпретированы им как согласующиеся с результатами Кауфмана[8]. Конкурирующие теории В 1902 году Макс Абрахам опубликовал теорию, основанную на предположении, что электрон представляет собой твёрдую идеальную сферу, заряд которой равномерно распределён по её поверхности. Как объяснялось выше, он ввёл так называемую «поперечную электромагнитную массу» помимо «продольной электромагнитной массы» и утверждал, что вся масса электрона имеет электромагнитное происхождение[A 6][A 7][9][10][11]. Между тем Лоренц (1899, 1904) расширил свою теорию электронов, предполагая, что заряд электрона распределён по всему его объёму, и что в опыте Кауфмана его форма будет сжиматься в направлении движения и оставаться неизменной в поперечных направлениях. К удивлению Кауфмана, Лоренц смог показать, что его модель также согласуется с его экспериментальными данными. Эта модель была дополнительно разработана и усовершенствована Анри Пуанкаре (1905 г.), так что теперь теория Лоренца согласовывалась с принципом относительности[A 8][A 9][12][13]. Аналогичная теория была развита Альфредом Бухерером и Паулем Ланжевеном в 1904 г. с той разницей, что общий объём, занимаемый деформированным электроном, считался неизменным. Оказалось, что предсказание этой теории ближе к теории Абрахама, чем к теории Лоренца[A 10][14]. Наконец, специальная теория относительности Альберта Эйнштейна (1905 г.) предсказала изменение массы точечного электрона за счёт свойств преобразования между системой покоя частицы и лабораторной системой, в которой проводились измерения. Математически этот расчёт предсказывает ту же зависимость между скоростью и массой, что и теория Лоренца, хотя и предполагает совсем другие физические концепции[A 11][15]. Что касается увеличения поперечной электромагнитной массы, предсказания различных теорий описываются следующими выражениями (рис. 3): Эксперименты 1905 годаЧтобы сделать выбор между этими теориями, Кауфманн снова провёл свои эксперименты с большей точностью. Кауфман считал, что он окончательно опроверг формулу Лоренца — Эйнштейна и, следовательно, также опроверг принцип относительности. По его мнению, единственными оставшимися вариантами были теории Абрахама и Бухерера. Лоренц был озадачен и написал, что он «на исходе своей латыни»[A 12][A 13][16][17]. Однако эксперимент Кауфмана подвергся критики[A 14][A 15]. Вскоре после того, как Кауфманн опубликовал свои результаты и выводы своего анализа, Макс Планк решил повторно проанализировать данные, полученные в ходе эксперимента. В 1906 и 1907 годах Планк опубликовал собственное заключение о поведении инерционной массы электронов с большими скоростями. Используя всего девять точек данных из публикации Кауфмана в 1905 году, он пересчитал точную настройку полей для каждой точки и сравнил измерения с предсказаниями двух конкурирующих теорий. Он показал, что результаты Кауфмана не являются полностью решающими и могут привести к сверхсветовым скоростям[18]. Эйнштейн заметил в 1907 году, что, хотя результаты Кауфмана лучше согласуются с теориями Абрахама и Бухерера, чем с его собственными, основания других теорий неправдоподобны и, следовательно, имеют лишь небольшую вероятность быть правильными. Последующие экспериментыБухерер
Основной проблемой экспериментов Кауфмана было использование им параллельных магнитных и электрических полей, на что указывал Адольф Бестельмейер (1907). Используя метод, основанный на перпендикулярных магнитных и электрических полях (введённый Дж. Дж. Томсоном и развитый до фильтра скоростей Вильгельмом Вином), Бестельмейер получил значительно отличающиеся значения отношения заряда к массе для катодных лучей вплоть до 0,3с. Однако Бестельмейер добавил, что его эксперимент не был достаточно точным, чтобы с определённостью выбрать правильную теорию[19]. Поэтому Альфред Бухерер в 1908 году провёл точное измерение, используя фильтр скоростей, аналогичный фильтру Бестельмейера. См. рис. 4 & 5. Бета-источник радия помещался в центр круглого конденсатора, состоящего из двух пластин из посеребрённого стекла, расположенных на расстоянии 0,25 мм друг от друга при наппряжении 500 вольт в однородном магнитном поле напряженностью 140 Гаусс. Радий излучал бета-лучи во всех направлениях, но в любом конкретном направлении α только те бета-лучи выходили из фильтра скоростей, скорость которых была такова, что электрическое и магнитное поля точно компенсировали друг друга. После выхода из конденсора лучи отклонялись магнитным полем и экспонировали фотопластинку, установленную параллельно краю конденсора и перпендикулярно неотклонённым лучам[20].   Для своего окончательного анализа Бухерер пересчитал измеренные значения пяти прогонов по формулам Лоренца и Абрахама соответственно, чтобы получить отношение заряда к массе, как если бы электроны находились в состоянии покоя. Поскольку для покоящихся электронов это отношение не меняется, точки данных должны располагаться на одной горизонтальной линии (см. 6). Однако это было примерно только в том случае, когда данные рассчитывались по формуле Лоренца, а результаты по формуле Абрагама резко отклонялись (красная и синяя линии — среднее значение по обеим формулам). Согласие с формулой Лоренца — Эйнштейна было истолковано Бухерером как подтверждение принципа относительности и теории Лоренца — Эйнштейна — результат, который сразу же приветствовали Лоренц, Эйнштейн и Герман Минковский[A 16][A 17]. Кроме того, установка Бухерера была усовершенствован в 1909 году его учеником Куртом Вольцем, который также получил согласие с формулой Лоренца — Эйнштейна (хотя и не сравнил формулу Абрахама со своими данными, рис. 7)[21]. Несмотря на то, что многие физики приняли результат Бухерера, всё же оставались некоторые сомнения[A 18][A 19]. Например, Бестельмейер опубликовал статью, в которой поставил под сомнение правильность результата Бухерера. Он утверждал, что один эксперимент сам по себе не может установить правильность важного физического закона, что результат Бухерера может быть значительно искажен некомпенсированными лучами, достигающими фотопластинки, и что необходимы обширные протоколы данных и анализ ошибок[22]. За полемическим спором между этими двумя учёными последовал ряд публикаций, в которых Бестельмейер утверждал, что на эксперименты Вольца влияют те же проблемы[23][24][25]. ГупкаВ отличие от Кауфмана и Бухерера, Карл Эрих Хупка (1909) использовал для своих измерений катодные лучи со скоростью 0,5c. Излучение (генерируемое на медном катоде) сильно ускорялось полем между катодом и анодом в высоковакуумной разрядной трубке. Анод, служащий диафрагмой, проходил луч с постоянной скоростью и рисовал теневое изображение двух проволочек Волластона на фосфоресцентном экране за второй диафрагмой. Если за этой диафрагмой генерировался ток, то луч отклонялся и теневое изображение смещалось. Результаты совпали с теорией Лоренца — Эйнштейна, хотя Хупка заметил, что этот эксперимент не даёт окончательного ответа[26]. Впоследствии В. Хайль опубликовал несколько статей, посвящённых критике и интерпретации результата, на которые ответил Хупка[27][28][29]. Нойман и Гюи/Лаванши В 1914 году Гюнтер Нойман провёл новые измерения с использованием оборудования Бухерера, в частности, внеся некоторые улучшения в ответ на критику Бестельмейера, особенно вопрос о нескомпенсированных лучах, и внёс значительные улучшения в протоколы данных. Метод расчёта был таким же, как у Бухерера (см. рис. 6). Также и в этом эксперименте данные, соответствующие формуле Лоренца, находятся почти на одной горизонтальной линии, как и требовалось, а данные, полученные по формуле Абрагама, резко отклоняются (см. рис. 8). Нейман пришёл к выводу, что его эксперименты согласуются с экспериментами Бухерера и Хупки, определённо доказав формулу Лоренца — Эйнштейна в диапазоне 0,4-0,7с, и опроверг формулу Абрахама. Инструментальные погрешности имели место в диапазоне 0,7-0,8с, поэтому отклонение от формулы Лоренца-Эйнштейна в этом диапазоне не считалось значимым[30].  В 1915 году Шарль Гюи и Шарль Лаванши измерили отклонение катодных лучей при скоростях 0,25-0,5 с. Они использовали трубку с катодом и анодом для ускорения лучей. Диафрагма на аноде создавала пучок, который отклонялся. В конце аппарата помещался экран, по которому попадания частиц фотографировались камерой. Впоследствии они вычислили отношение поперечной электромагнитной массы mT к массе покоя m0, обозначенное красной и синей кривыми, и получили хорошее согласие с формулой Лоренца — Эйнштейна (см. рис. 9), дополняющей результат Ноймана[31][32]. Многие считали, что эксперименты Ноймана и Гюи/Лаванши окончательно доказывают формулу Лоренца — Эйнштейна[A 20][A 21][A 22]. Лоренц резюмировал эти усилия в 1915 году[A 23]:
Дальнейшее развитие Zahn & Spees (1938)[33] и Faragó & Лайош Яноши (1954)[34] утверждали, что многие предположения, использованные в этих ранних экспериментах относительно природы и свойств электронов и экспериментальной установки, были неверными или неточными. Как и в случае с экспериментами Кауфмана, эксперименты Бухерера — Ноймана показали бы только качественное увеличение массы и не могли сделать выбор между конкурирующими теориями[A 24][A 25]. В то время как результаты этих экспериментов по отклонению электронов долгое время оспаривались, исследования тонкой структуры водородных линий Карлом Глитчером (на основе работ Арнольда Зоммерфельда) уже в 1917 г. дали чёткое подтверждение формулы Лоренца — Эйнштейна, потому что релятивистские выражения для импульса и энергии были необходимы для вывода тонкой структуры, и представляли собой опровержение теории Абрахама[35][A 26]. 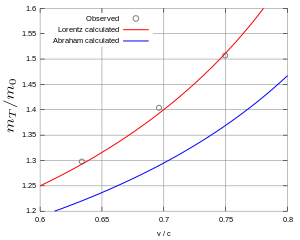 Кроме того, первые эксперименты по отклонению электронов с достаточной точностью были проведены Роджерсом и др. (1940), разработавший усовершенствованную установку. Ряд распада радия даёт спектр бета-частиц с широким диапазоном энергий. В более ранних измерениях Кауфмана, Бухерера и других использовались плоские конденсаторы с параллельными пластинами, которые не обеспечивали фокусировки бета-частиц. Роджерс и др. (Рис. 10) вместо этого построил электростатический спектрограф, способный разрешать максимумы энергии отдельных линий бета-частиц из ряда распада радия. Электростатический спектрограф был сконструирован из сегментов двух цилиндров и заключён в вакуумную железную камеру. Бета-лучи испускаются тонкой платиновой проволокой, покрытой активным напылением радия. Рассеянные лучи падали на щель перед счётчиком Гейгера. Данные этого эксперимента были объединены с предыдущими измерениями Hρ с помощью магнитного спектрометра, чтобы получить отношение заряда к массе, которое впоследствии было сопоставлено с предсказаниями Лоренца и Абрахама для отношения поперечной массы и массы покоя. Все точки располагались на кривой, представляющей формулу Лоренца — Эйнштейна, с точностью до 1 % (см. рис. 11)[36]. Этот эксперимент считается достаточно точным, чтобы различать теории[A 27]. Современные тестыС тех пор было проведено множество дополнительных экспериментов, касающихся релятивистского соотношения энергии и импульса, включая измерения отклонения электронов, и все они подтвердили специальную теорию относительности с высокой точностью. Также в современных ускорителях частиц регулярно подтверждаются предсказания специальной теории относительности. ПримечанияПервичные источники
Вторичные источники
Литература
|



![{\displaystyle \phi (\beta )={\frac {3}{4\beta ^{2}}}\left[{\frac {1}{\beta }}\lg {\frac {1-\beta }{1+\beta }}+{\frac {2}{1-\beta ^{2}}}\right],\;\beta ={\frac {v}{c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a76587532865bf01653d4c4f8b77572cb8006ea9)



