Число Стралера — Философова

Диаграмма порядка потоков Стралера

Число Стралера, число Хортона — Стралера или число Стралера — Философова[1] математического дерева — это численная мера сложности ветвления.

Эти числа впервые были введены в гидрологии Робертом Хортоном (англ.)[2] в 1945. Стралер[3][4] и, независимо, Философов предложили использовать дихотомическое деление рек на порядки (как предложил Хортон), но ими не принята процедура перекодировки русел для выявления системы главных рек[1]. В этом приложении числа называются порядком потоков Стралера и используются для определения размера потока, основываясь на иерархии притоков. Числа появляются также при анализе L-систем и в иерархических биологических структурах, таких как (биологические) деревья и дыхательные и кровеносные системы, в распределении регистров при компиляции высокоуровневых языков программирования и в анализе социальных сетей. Альтернативную систему порядка потоков[англ.] разработали Шрив[5][6] и группа Ходжкинсона[7]. Статистическое сравнение систем Стралера и Шрива вместе с анализом длин потоков дал Смарт[8].

Определение

Все деревья в контексте статьи являются ориентированными графами, направленными от корня к листьям. Другими словами, они являются ориентированными деревьями. Степень узла в дереве — это просто число потомков узла. Можно назначить числа Стралера всем узлам дерева снизу вверх следующим образом:

  • Если узел является листом (не имеет потомков), его число Стралера равно единице.
  • Если узел имеет одного потомка с числом Стралера i, а все остальные потомки имеют число Стралера, меньшее i, то число Стралера узла снова равно i.
  • Если узел имеет два или больше потомков с числом Стралера i и не имеет потомков с бо́льшим числом, то число Стралера узла равно i + 1.

Число Стралера дерева равно числу Стралера его корневого узла.

Алгоритмически эти числа можно назначить путём осуществления поиска в глубину и назначения каждому узлу числа Стралера в обратном порядке. Те же самые числа могут быть сгенерированы путём подрезки, в процессе которого дерево упрощается в результате последовательности этапов. На каждом этапе удаляются все висячие узлы и все пути со степенью единица, ведущих к листьям — число Стралера узла равно номеру этапа, на котором узел удаляется, а число Стралера дерева равно числу этапов, требующихся для удаления всех узлов. Другое эквивалентное определение Стралера дерева — это высота наибольшего полного двоичного дерева, которое может быть гомеоморфно вложено в данное дерево. Число Стралера узла в дереве аналогично высоте наибольшего полного дерева, которое можно вложить ниже этого узла.

Любой узел с числом Стралера i должен иметь по меньшей мере два наследника с числом Стралера i − 1, по меньшей мере четыре наследника с числом Стралера i − 2, и т. д. и по меньшей мере 2i − 1 листовых наследников. Таким образом, в дереве с n узлами наибольшее значение числа Стралера равно log2 n + 1[9]. Однако, если дерево не образует полное бинарное дерево, его число Стралера будет меньше этой величины. В двоичном дереве с n узлами, выбранном случайно из всех возможных бинарных деревьев с равномерной вероятностью, ожидаемый индекс корня с большой вероятностью очень близок к log4 n[10][9].

Приложения

Речная сеть

В приложении порядков потоков[англ.] Стралера в гидрологии каждый сегмент потока или реки трактуется как узел в дереве. Когда два потока первого порядка сливаются, они образуют поток второго порядка. Когда сливаются потоки второго порядка, они образуют поток третьего порядка. Когда потоки меньшего порядка вливаются в поток с большим порядком, порядки потоков не меняются. Таким образом, если поток первого порядка вливается в поток второго порядка, второй поток остаётся потоком второго порядка. Но если поток второго порядка вливается в поток того же порядка, второй становится потоком третьего порядка. Так, для математических деревьев сегмент с индексом i должен иметь по меньшей мере 2i − 1 различных источников порядка 1. Шрив заметил, что законы Хортона и Стралера следует ожидать в любом топологически случайном распределении. Последующие исследования связей подтвердили эти аргументы, установив, что нельзя объяснить структуру или источники потоков[7][11].

Водный поток должен быть (как гидрологическое явление) либо пересыхающим, либо не пересыхающим[англ.]. Пересыхающие (или «перемежающиеся») потоки имеют воду в русле лишь часть года. Индекс потока может иметь значение от 1 (поток без притоков) до 12 (наиболее мощные реки, такие как Амазонка в устье). Огайо имеет порядок 8, а Миссисипи имеет порядок 10. По оценкам около 80 % потоков планеты имеют порядок от единицы до трёх[12]

Если отношение бифуркации водных потоков малы, то имеется высокий шанс наводнения, поскольку вода будет собираться в один канал, а не рассредотачиваться, как в случае высокого отношения бифуркации. Отношение бифуркации может также показать, какие части речного бассейна более опасны (с точки зрения возможности наводнения). Большинство рек Британии имеют отношения бифуркации между 3 и 5[13].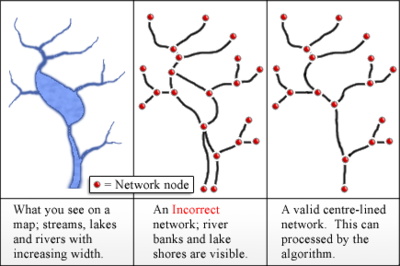

Сравнение неправильного и правильного сведения водной системы в древовидную сеть

Глейзер, Денисюк, Риммер и Салингар[14] описали, каким образом вычислить значение порядка потока Стралера в GIS. Этот алгоритм имплементирован в системе RivEX, инструментальной системе ArcGIS 10.2.1 компании ESRI. Входом в их алгоритм служит сеть центральных линий водных потоков, представленная дугами (или рёбрами), связывающими узлы. Границы озёр и берега рек не следует использовать в качестве дуг, поскольку, в общем случае, они образуют сеть с неправильной топологией.

Другие иерархические системы

Нумерацию Стралера можно применить к статистическому анализу любой иерархической системы, не только рек.

  • Аренас, Данон, Диаз-Гилера и Глейзер[15] описывают применение индекса Хортона — Стралера для анализа социальных сетей.
  • Эренфойхт, Розенберг и Вермьер[16] применили вариант нумерации Стралера (начиная нумерацию для листьев с нуля, а не с единицы), который они назвали рангом дерева, для анализа L-систем.
  • Нумерация Стралера применяется также в биологических иерархиях, таких как структура ветвления деревьев[17], дыхательных и кровеносных систем животных[18].

Распределение регистров

При трансляции высокоуровневых языков программирования в язык ассемблера минимальное число регистров, требуемых для выполнения дерева выражения, в точности равно его числу Стралера. В этом контексте число Стралера может называться числом регистров[19][20].

Для деревьев выражений, требующих больше регистров, чем доступно, может быть использован алгоритм Сети — Ульмана, чтобы преобразовать дерево выражения в последовательность машинных инструкций, которая использует регистры настолько эффективно, насколько это возможно, минимизируя число промежуточных записей регистров в основную память и общее число инструкций в откомпилированном коде.

Связанные параметры

Отношение бифуркации

Связаны с числами Стралера для деревьев отношения бифуркации, описывающие близость дерева к сбалансированному дереву. Для каждого порядка i в иерархии i-ое отношения бифуркации равно

,

где ni означает число узлов порядка i.

В качестве отношения бифуркации всей иерархии можно взять среднее отношений бифуркации. В полном бинарном дереве отношение бифуркации будет равно 2, но другие деревья будут иметь меньшее значение отношения бифуркации. Отношение бифуркации — величина безразмерная.

Путевая ширина

Путевая ширина произвольного неориентированного графа G может быть определена как наименьшее число w, такое, что существует интервальный граф H, содержащий G в качестве подграфа, такой, что наибольшая клика графа H имеет w + 1 вершин. Для деревьев (рассматриваемых как неориентированные графы путём игнорирования ориентации и корня) путевая ширина может отличаться от числа Стралера, но с ним тесно связана — в дереве с путевой шириной w и числом Стралера s эти две величины связаны неравенством[21]

w ≤ s ≤ 2w + 2.

Возможность работы с графами, имеющими цикл, а не только с деревьями, дают путевой ширине дополнительную гибкость по сравнению с числом Стралера. Однако, в отличие от числа Стралера, путевая ширина определена только для всего графа, а не для каждого узла в графе.

Примечания

  1. ↑ 1 2 Ананьев, Симонов, Спиридонов, 1992, с. 102.
  2. ↑ Horton, 1945.
  3. ↑ Strahler, 1952.
  4. ↑ Strahler, 1957.
  5. ↑ Shreve, 1966, с. 17–37.
  6. ↑ Shreve, 1967, с. 178–186.
  7. ↑ 1 2 Hodgkinson, McLoughlin, Cox, 2006, с. 394–407.
  8. ↑ Smart, 1968, с. 1001–1014.
  9. ↑ 1 2 Devroye, Kruszewski, 1996.
  10. ↑ Devroye, Kruszewski, 1995.
  11. ↑ Kirchner, 1993, с. 591–594.
  12. ↑ [geography.about.com/od/physicalgeography/a/streamorder.htm Stream Order – The Classification of Streams and Rivers]. Дата обращения: 11 декабря 2011.
  13. ↑ Waugh, 2002.
  14. ↑ Gleyzer, Denisyuk, Rimmer, Salingar, 2004.
  15. ↑ Arenas, Danon, Díaz-Guilera, Gleiser, Guimerá, 2004.
  16. ↑ Ehrenfeucht, Rozenberg, Vermeir, 1981.
  17. ↑ Borchert, Slade, 1981.
  18. ↑ Horsfield, 1976.
  19. ↑ Ершов, 1958.
  20. ↑ Flajolet, Raoult, Vuillemin, 1979.
  21. ↑ Люттенбергер и Шлунд (Luttenberger, Schlund 2011) использовали определение «размерности» дерева, которая на единицу меньше числа Стралера.

Литература

  • Kirchner J.W. Statistical inevitability of Horton Laws and the apparent randomness of stream channel networks // Geology. — 1993. — Вып. 21.
  • Динамическая геоморфология: Учебное пособие / Ананьев Г.С., Симонов Ю.Г., Спиридонов А.И.. — М.: Изд-во МГУ, 1992. — ISBN 5-211-01618-1.
  • Shreve R.L. Statistical law of stream numbers // Journal of Geology. — 1966. — Вып. 74.
  • Shreve R.L. Infinite topologically random channel networks // Journal of Geology. — 1967. — Вып. 75.
  • Hodgkinson J.H., McLoughlin S., Cox M.E. The influence of structural grain on drainage in a metamorphic sub-catchment: Laceys Creek, southeast Queensland, Australia // Geomorphology. — 2006. — Вып. 81.
  • Smart J.S. Statistical properties of stream lengths // Water Resources Research,. — 1968. — Т. 4, вып. 5.
  • Arenas A., Danon L., Díaz-Guilera A., Gleiser P. M., Guimerá R. Community analysis in social networks // European Physical Journal B. — 2004. — Т. 38, вып. 2. — С. 373–380. — doi:10.1140/epjb/e2004-00130-1.
  • Rolf Borchert, Norman A. Slade. Bifurcation ratios and the adaptive geometry of trees // Botanical Gazette. — 1981. — Т. 142, вып. 3. — С. 394–401. — doi:10.1086/337238. — JSTOR 2474363.
  • Luc Devroye, Paul Kruszewski. A note on the Horton–Strahler number for random trees // Information Processing Letters. — 1995. — Т. 56, вып. 2. — С. 95–99. — doi:10.1016/0020-0190(95)00114-R.
  • Devroye L., Kruszewski P. On the Horton–Strahler number for random tries // RAIRO Informatique Théorique et Applications. — 1996. — Т. 30, вып. 5. — С. 443–456.
  • Ehrenfeucht A., Rozenberg G., Vermeir D. On ETOL systems with finite tree-rank // SIAM Journal on Computing. — 1981. — Т. 10, вып. 1. — С. 40–58. — doi:10.1137/0210004.
  • Ershov A. P. On programming of arithmetic operations // Communications of the ACM. — 1958. — Т. 1, вып. 8. — С. 3–6. — doi:10.1145/368892.368907.
    • Ершов А.П. О программировании арифметических операторов // Доклады АН СССР. — 1958. — Т. 118,, вып. 3. — С. 427–430.
  • Flajolet P., Raoult J. C., Vuillemin J. The number of registers required for evaluating arithmetic expressions // Theoretical Computer Science. — 1979. — Т. 9, вып. 1. — С. 99–125. — doi:10.1016/0304-3975(79)90009-4.
  • Gleyzer A., Denisyuk M., Rimmer A., Salingar Y. A fast recursive GIS algorithm for computing Strahler stream order in braided and nonbraided networks // Journal of the American Water Resources Association. — 2004. — Т. 40, вып. 4. — С. 937–946. — doi:10.1111/j.1752-1688.2004.tb01057.x.
  • Keith Horsfield. Some mathematical properties of branching trees with application to the respiratory system // Bulletin of Mathematical Biology. — 1976. — Т. 38, вып. 3. — С. 305–315. — doi:10.1007/BF02459562. — PMID 1268383.
  • Horton R. E. Erosional development of streams and their drainage basins: hydro-physical approach to quantitative morphology // Geological Society of America Bulletin. — 1945. — Т. 56, вып. 3. — С. 275–370. — doi:10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2..
  • Lanfear K. J. A fast algorithm for automatically computing Strahler stream order // Journal of the American Water Resources Association. — 1990. — Т. 26, вып. 6. — С. 977–981. — doi:10.1111/j.1752-1688.1990.tb01432.x.
  • Michael Luttenberger, Maxmilian Schlund. An extension of Parikh’s theorem beyond idempotence. — 2011. — arXiv:1112.2864.
  • Strahler A. N. Hypsometric (area-altitude) analysis of erosional topology // Geological Society of America Bulletin. — 1952. — Т. 63, вып. 11. — С. 1117–1142. — doi:10.1130/0016-7606(1952)63[1117:HAAOET]2.0.CO;2.
  • Strahler A. N. Quantitative analysis of watershed geomorphology // Transactions of the American Geophysical Union. — 1957. — Т. 38, вып. 6. — С. 913–920. — doi:10.1029/tr038i006p00913.
  • David Waugh. Geography, An Integrated Approach. — 2002.