Статистическая мощность

Статистическая мощность в математической статистике — вероятность отклонения основной (или нулевой) гипотезы при проверке статистических гипотез в случае, когда конкурирующая (или альтернативная) гипотеза верна. Чем выше мощность статистического теста, тем меньше вероятность совершить ошибку второго рода. Величина мощности также используется для вычисления размера выборки, необходимой для подтверждения гипотезы с необходимой силой эффекта.

Применение

Величина мощности при проверке статистической гипотезы зависит от следующих факторов:

• величины уровня значимости, обозначаемого греческой буквой ${\displaystyle \alpha }$, на основании которого принимается решение об отвержении или принятии альтернативной гипотезы;
• величины эффекта (то есть разности между сравниваемыми средними);
• размера выборки, необходимой для подтверждения статистической гипотезы.

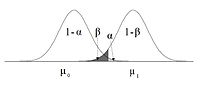
Основные параметры для определения мощности показаны на схеме.

Статистическая мощность

Уровень значимости (${\displaystyle \alpha }$) выбирается исследователем и определяет вероятность совершения ошибки первого рода. Вероятность того, что альтернативная гипотеза верна, но решение принимается в пользу нулевой гипотезы (ошибка второго рода), обозначается греческой буквой ${\displaystyle \beta }$. Тогда вероятность принятия правильного решения при истинной альтернативной гипотезе (мощность) равна ${\displaystyle 1-\beta }$.

При известном стандартном отклонении генеральной совокупности и заданном уровне значимости ${\displaystyle \alpha =0{,}05}$ мощность ${\displaystyle 1-\beta }$ можно вычислить с использованием Z-критерия по формуле

${\displaystyle {1-\beta }=P\left(Z>{\frac {\mu {_{0}}+1{,}64(SE)-\mu _{1}}{SE}}\right)}$,

где ${\displaystyle \mu {_{0}}}$ есть среднее при нулевой гипотезе, ${\displaystyle \mu {_{1}}}$ — среднее при альтернативной гипотезе, ${\displaystyle 1{,}64}$ — величина критического значения Z-статистики при одностороннем Z-тесте, и ${\displaystyle SE}$ — стандартная ошибка.

Величина эффекта определяет вероятность совершения ошибки второго рода. Коэффициент величины эффекта называется мерой эффекта ${\displaystyle d}$. Был введён в употребление Дж. Коэном и вычисляется как отношения разности между сравниваемыми средними к стандартному отклонению ${\displaystyle d={\frac {\mu {_{0}}-\mu {_{1}}}{\sigma }}}$.

Размер выборки, необходимой для подтверждения статистической гипотезы, влияет на статистическую мощность, так как с увеличением выборки уменьшается стандартная ошибка, а следовательно, увеличивается мощность.

См. также

• Проверка статистических гипотез
• Ошибки первого и второго рода
• Статистический критерий
• Уровень значимости

Литература

• Кендалл М., Стьюарт А. Статистические выводы и связи. — М.: Наука, 1973.
• Hays, W. Statistics (5th ed.). Cengage Learning, 1994.