|
Сеть КлозаСеть Клоза (иногда сеть Клоса) — вид многокаскадной (по другой терминологии — многоярусной[1]) коммутационной сети, впервые формально описанной Чарльзом Клозом в 1953 году[2]. Такая сеть представляет собой теоретический вариант практической многокаскадной телефонной коммутационной системы. Общее описание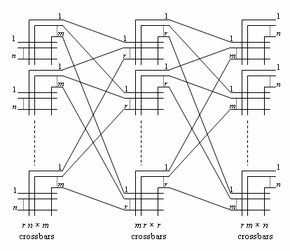 Сеть Клоза имеет три каскада (яруса): входной каскад, промежуточный (средний) каскад и выходной каскад. Каждый каскад состоит из ряда перекрёстных коммутаторов — т. наз. «кроссбаров», или, по другой терминологии, коммутационных элементов (КЭ)[3][4], как показано далее на рисунке. Каждый вызов (запрос на соединение) попадает на входящий КЭ, после чего может быть направлен через любой доступный КЭ среднего яруса на соответствующий исходящий КЭ. При этом КЭ среднего яруса доступен для нового вызова в том случае, если свободны как линия, соединяющая его со входящим КЭ, так и линия, соединяющая его с исходящим КЭ. Ключевое преимущество сетей Клоза состоит в том, что они имеют гораздо меньшее количество точек коммутации по сравнению с перекрёстным коммутатором. В практическом смысле сеть Клоза была очень выгодна для реализации в электромеханических телефонных станциях, но с приходом СБИС её ценность уменьшилась, хотя её принципы использовались и в цифровых быстрых коммутаторах пакетов, например, в коммутаторе ATOM фирмы NEC[5][6]. Сеть Клоза определяется тремя целыми числами n, m, и r. Число n равно количеству линий, подключённых к каждому из r КЭ входящего каскада. Каждый КЭ входящего каскада имеет m выходов, и средний каскад также содержит m КЭ. Таким образом, размерность КЭ входящего каскада будет n x m, то есть n входов и m выходов. Существует строго одно соединение между каждым КЭ входящего каскада и каждым КЭ среднего каскада, то же самое верно и для соединений среднего каскада с исходящим каскадом. Исходящий (третий) каскад содержит r КЭ, каждый из которых имеет размерность m x n. Вероятности блокировкиВероятности блокировки сети Клоза определяются относительными величинами m и n. Строго неблокирующие сети Клоза (m ≥ 2n — 1) — оригинальная выкладка Клоза 1953 годаЕсли m ≥ 2n — 1, то сеть Клоза является строго неблокирующей в том смысле, что свободный вход входящего КЭ всегда может быть соединён со свободным выходом исходящего КЭ без необходимости перекоммутации уже существующих соединений. Этот вывод составляет основу классической статьи Клоза 1953 года. Предположим, что имеется свободная линия на входящем КЭ, которая должна быть соединена со свободной линией на конкретном исходящем КЭ. В наихудшем случае входящий КЭ уже обслуживает n — 1 соединение, то же самое можно сказать и про исходящий КЭ, то есть, что он обслуживает n — 1 соединение. Предположим, также для наихудшего случая, что каждое из этих соединений проходит через отличный КЭ среднего яруса. Следовательно, в наихудшем случае 2n — 2 КЭ среднего яруса не способны установить новое соединение. Таким образом, чтобы сеть Клоза была строго неблокирующей, требуется ещё один КЭ среднего яруса, и всего их число должно составить 2n — 1. Сети Клоза, неблокирующие при перекоммутациях (m ≥ n)Если m ≥ n, то сеть Клоза называется «неблокирующей при перекоммутациях». Это означает, что свободный порт входного КЭ всегда может быть соединён со свободным портом выходного КЭ, но для этого, возможно, потребуется перекоммутировать уже существующие соединения, установив их через другие КЭ центрального (среднего) каскада сети Клоза[7]. Для доказательства этого положения достаточно рассмотреть случай с m = n, когда сеть Клоза задействована полностью, то есть, обслуживается r×n соединений. Доказательство показывает, как любая перестановка r×n входных линий для r×n выходных линий может быть разбита на меньшие перестановки, каждая из которых может быть реализована отдельным КЭ в сети Клоза, где m = n. В доказательстве используется теорема Холла[8], названная «брачной теоремой», по причине её разъяснения с привлечением «мальчиков» и «девочек». Так, предполагается, что имеется r мальчиков и r девочек. Теорема устанавливает, что если в подмножестве из k мальчиков (для каждого k, так что 0 ≤ k ≤ r) каждый мальчик знаком с k или больше девочками, тогда каждый мальчик может жениться на девочке, с которой он знаком. Ясно, что это необходимое условие для того, чтобы имела место свадьба, и, удивительно то, что этого и достаточно. В контексте сети Клоза каждый мальчик — это входящий КЭ, а каждая девочка — исходящий КЭ. Говорят, что мальчик знаком с девочкой в том случае, когда входящий и исходящий КЭ обслуживают одно и то же соединение. Каждое множество из k мальчиков должно быть знакомым, по крайней мере, с k девочками, потому что k входящих КЭ обслуживают k×n соединений, и для их обслуживания требуется не менее, чем k исходящих КЭ. Отсюда каждый входящий КЭ составит пару с исходящим КЭ, который обслуживает то же самое соединение «один к одному». Эти r соединений могут быть обслужены одним КЭ среднего яруса. Если теперь удалить этот КЭ среднего яруса из сети Клоза, то m уменьшается на 1, и мы имеем меньшую сеть Клоза. Затем процесс повторяется снова, до тех пор пока m не станет равно 1, и каждое соединение будет обслуживаться КЭ среднего каскада. Вероятности блокировки — приближения Ли и ЯкобеусаРеальные телефонные коммутационные системы редко бывают строго неблокирующими по причине высокой стоимости их реализации, обычно они отличаются невысокой вероятностью блокировки, которую можно рассчитать с помощью приближений Ли или Якобеуса[9] при условии невыполнения перекоммутаций существующих соединений. В данном случае потенциальное количество других активных соединений в каждом входном или выходном коммутаторе будет u = n — 1. В приближении Ли предполагается, что каждая внутренняя линия между каскадами уже занята соединением с вероятностью p, и что эта линия полностью независима от других линий. В этом случае вероятность блокировки будет переоценена, особенно для небольших r. Вероятность того, что данная внутренняя линия занята составляет p = uq/m, где q равна вероятности занятости входящей или исходящей линии. Наоборот, вероятность того, что линия свободна, составляет 1 — p. Вероятность того, что путь, соединяющий входящий КЭ с исходящим КЭ через КЭ среднего яруса, свободен, равна вероятности того, что обе линии свободны, а именно (1 — p)2. Следовательно, вероятность его недоступности составит величину 1 — (1 — p)2. Вероятность блокировки, или вероятность того, что нет таких свободных путей, составит тогда [1 — (1 — p)2]m. Приближение Якобеуса более точное, и для того, чтобы показать, как оно выводится, предположим, что КЭ среднего каскада уже обслуживают определённое количество вызовов. Это отражает тот факт, что только «относительные» конфигурации входящих и исходящих КЭ имеют значение. Имеется i соединений, входящих в сеть через один и тот же входящий КЭ, и свободные линии должны быть выделены на их обслуживание, и имеется j соединений, выходящих из сети Клоза через один и тот же исходящий КЭ, и для их обслуживания также требуется задействовать свободные линии. Следовательно, 0 ≤ i ≤ u, и 0 ≤ j ≤ u. Пусть A будет равно числу способов коммутации j соединений, исходящих на m КЭ среднего яруса. Пусть B будет равно числу этих способов коммутации, что выражается в блокировке. Это равно числу случаев, при которых оставшиеся m — j КЭ среднего каскада совпадают с m — j из i входящих соединений, что является числом подмножеств, содержащих m — j из этих соединений. Тогда вероятность блокировки составит: Если fi является вероятностью того, что i других соединений уже обслуживаются входящим КЭ, а gj равна вероятности того, что j других соединений уже обслуживаются исходящим КЭ, то общая вероятность блокировки составит: Её можно рассчитать с помощью величин fi и gj, каждая из которых отличается биномиальным распределением. После алгебраических преобразований вероятность блокировки может выражена как: Сети Клоза, имеющие более трёх каскадовСеть Клоза можно построить из любого количества нечётных каскадов. Путём замены каждого КЭ центрального яруса 3-каскадной сетью Клоза, мы получим 5-каскадную сеть Клоза. Повторяя этот процесс, можно получить сети Клоза, состоящие из 7, 9, 11 и так далее каскадов. Сеть Бенеша (m = n = 2)Неблокирующая при перекоммутациях сеть этого типа, где m = n = 2, в общем случае называется «сетью Бенеша», и даже те сети, которые анализировались и обсуждались до него. Число входов и выходов такой сети составляет N = r×n = 2r. Такие сети имеют каскадов, каждый из которых состоит из N/2 КЭ 2×2. Далее показана сеть Бенеша 8×8 (то есть, где N = 8); она имеет 5 каскадов, каждый из которых содержит N/2 = 4 КЭ 2×2, и всего эта сеть содержит 20 КЭ 2×2. Три центральные каскада состоят из двух меньших сетей Бенеша 4×4, в то время как в центральном каскаде каждый из КЭ 2×2 можно рассматривать как сеть Бенеша 2×2. На этом примере видна рекурсивная составляющая сетей такого типа. 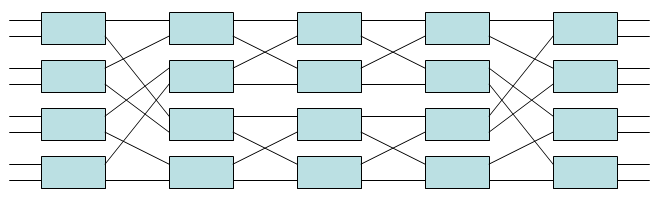 Литература
Примечания
|





