|
Рассада (игра)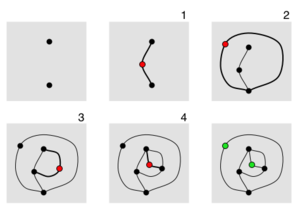 «Рассада» («ростки», англ. Sprouts) — топологическая игра, заключающаяся в том, что игроки (обычно двое) по определённым правилам рисуют линии на бумаге. Правила игрыПеред началом игры на бумаге рисуется несколько точек[1] — их можно назвать семенами, количество первоначальных точек оговаривается перед игрой. Затем игроки по очереди ходят. Каждый ход игрока состоит в том, что он либо соединяет две точки линией (прямой или кривой), либо рисует линию-петлю, начинающуюся в какой-нибудь точке и в этой же точке заканчивающуюся («рассада прорастает»). На каждой проведённой линии рисуется одна новая точка; новые точки равноправны первоначальным (от них также можно проводить линии, на каждой из которых также рисуется по одной точке).[2] При этом должны соблюдаться следующие правила:
Проигрывает тот игрок, который не сможет сделать ход, когда в очередной раз наступит его очередь ходить. Можно также играть в поддавки — в этом случае тот, кто сходит последним, считается не выигравшим, а, наоборот, проигравшим. Анализ игры «Рассада»Известна формула, с помощью которой, зная первоначальное количество точек, можно вычислить максимально возможное количество ходов всех игроков:
где К — максимально возможное количество ходов; Эта формула, однако, даёт лишь оценку сверху для максимально возможного количества ходов. На практике же, любой игрок может уменьшить возможное количество ходов, проводя замкнутые линии, изолируя тем самым одни точки от других и не давая соединять точки внутри замкнутой линии с точками снаружи. Известна также оценка снизу: игра не может закончиться раньше, чем через 2N ходов.[3] История игрыСоздателями игры «Рассада» являются профессор Джон Хортон Конвей и кембриджский аспирант Майкл Стьюарт Патерсон[англ.]. Игра «Рассада» была придумана ими 21 февраля 1967 года. Практически сразу игра стала популярной, по крайней мере в Кембриджском университете. Шуточная псевдоигра «Брюссельская капуста» Позднее Конвей изобрёл другую игру, точнее псевдоигру, похожую на «Рассаду». Желая подчеркнуть, что речь идёт об игре-шутке, он назвал вторую «игру» «Брюссельская капуста» (по-английски игра рассада называется «sprouts», брюссельская капуста — «Brussels sprouts»). В «Брюссельской капусте» перед игрой вместо нескольких точек рисуется несколько маленьких крестиков (у каждого крестика четыре коротких луча одинаковой длины). Каждый ход представляет собой соединение линией двух свободных лучей крестиков (лучей разных крестиков или одного). Каждый луч можно использовать для хода только один раз (после того как от луча провели линию, луч считается несвободным и ходить от него больше нельзя). Как и в рассаде, линии не должны пересекаться. Нельзя проходить «транзитом» через ранее поставленные крестики, не являющиеся началом и концом линии. Каждую проведённую линию пересекают короткой чёрточкой, то есть создают на этой линии новый крестик, у которого два противоположных луча лежат на только что проведённой линии, а другие два противоположных луча свободны. Выигрыш в «Брюссельской капусте» определяется так же, как в рассаде. Строго говоря, «Брюссельская капуста» не является игрой, так как количество ходов в ней не зависит от мастерства игроков: как бы игроки ни ходили, «игра» всегда заканчивается через 5N-2 хода (где N — количество первоначальных крестиков). Поэтому «Брюссельская капуста» не годится для состязания, «гимнастики ума» — она годится для того, чтобы, затеяв её, заранее предсказать или заключить беспроигрышное пари на то, кто выиграет (естественно, так подшутить можно только над тем, кто не знает свойств «Брюссельской капусты»). Литература
Примечания
|
