|
Гиперболическая точка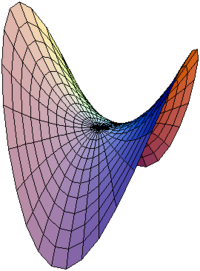 Гиперболическая точка поверхности — в дифференциальной геометрии точка двухмерной поверхности, в которой гауссова кривизна поверхности отрицательна. В гиперболической точке главные кривизны имеют противоположный знак[1]. Связанные определенияСедловая точка поверхностиСедловая точка поверхности — такая точка, что поверхность лежит локально по разные стороны от своей касательной плоскости проведённой в этой точке. Для дважды непрерывно дифференцируемой поверхности из этого следует, что гауссова кривизна в этой точке неположительна. Любая гиперболическая точка является седловой[2]. Некоторые авторы используют термин «седловая точка поверхности» как синоним для «гиперболическая точка поверхности»[1]. Седловая поверхностьПоверхность, у которой каждая точка является гиперболической, называется седловой поверхностью. Примечания
|