|
Битовая операция
Би́товая опера́ция в программировании — операция над цепочками битов, как правило в этот класс включаются логические побитовые операции и битовые сдвиги. Применяются в языках программирования и цифровой технике, изучаются в дискретной математике. Битовые операции лежат в основе обработки цифровых сигналов: посредством их из одного или нескольких сигналов на входе получается новый сигнал, который в свою очередь может быть подан на вход одной или нескольким таким операциям. Именно битовые операции в сочетании с запоминающими элементами (например триггерами) реализуют всё богатство возможностей современной цифровой техники. Побитовые операцииРяд источников по языкам низкого уровня называет побитовые логические операции просто логическими[1][2], но в терминологии программирования на языках высокого уровня в названиях битовых операций присутствуют прилагательные битовый, побитовый (например: «побитовое логическое И», оно же «побитовое умножение»), поразрядный. В некоторых языках программирования названия операторов, соответствующих логическим и побитовым логическим операциям, похожи. Кроме того, язык программирования может допускать неявное приведение числового типа к логическому и наоборот. В таких языках программирования необходимо внимательно следить за использованием логических и побитовых операций, перемешивание которых может привести к ошибкам. Например, в C++ результатом выражения «2 && 1» (логическое И) является булево значение true, а результатом выражения «2 & 1» (побитовое И) — целое значение 0. Побитовое отрицаниеПобитовое отрицание (или побитовое НЕ, дополнение) — унарная операция, действие которой эквивалентно применению логического отрицания к каждому биту двоичного представления операнда. Другими словами, на той позиции, где в двоичном представлении операнда был 0, в результате будет 1, и, наоборот, где была 1, там будет 0. Например:
Побитовое ИПобитовое «И» — бинарная операция, действие которой эквивалентно применению логического «И» к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, если оба соответствующих бита операндов равны 1, результирующий двоичный разряд равен 1; если же хотя бы один бит из пары равен 0, результирующий двоичный разряд равен 0. Пример:
Побитовое ИЛИПобитовое «ИЛИ» — бинарная операция, действие которой эквивалентно применению логического «ИЛИ» к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, если оба соответствующих бита операндов равны 0, двоичный разряд результата равен 0; если же хотя бы один бит из пары равен 1, двоичный разряд результата равен 1. Пример:
Побитовое исключающее ИЛИ (XOR)Побитовое исключающее «ИЛИ» (сложение по модулю 2) — бинарная операция, действие которой эквивалентно применению логического исключающего «ИЛИ» к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, если оба соответствующих бита операндов равны между собой, двоичный разряд результата равен 0; в противном случае, двоичный разряд результата равен 1. Пример:
Первое русское название операции обусловлено тем, что результат данной операции отличается от результата «ИЛИ» только в одном случае из 4 случаев входа — обоих 1 (случай одновременной истинности аргументов «исключается»). Ещё в русской грамматике значение данной логической связки передаётся союзом «либо». Второе название — тем, что действительно является сложением в кольце вычетов по модулю два, из чего следуют некоторые интересные свойства. Например, в отличие от вышеописанных «И» и «ИЛИ», данная операция является обратимой: . В компьютерной графике «сложение по модулю два» применяется при выводе спрайтов на картинку — повторное её применение убирает спрайт с картинки. Благодаря инволютивности эта же операция нашла применение в криптографии как простейшая реализация абсолютно стойкого шифра (шифра Вернама). «Сложение по модулю два» также может использоваться для обмена двух переменных, используя алгоритм обмена при помощи исключающего ИЛИ. Также данная операция может называться «инверсией по маске», то есть у исходного двоичного числа инвертируются биты, которые совпадают с 1 в маске. В распространённых языках программирования встроенными средствами реализуются только четыре побитовые логические операции: И, ИЛИ, НЕ и исключающее ИЛИ. Для задания произвольной побитовой логической операции вполне достаточно перечисленных, и, более того, как следует из теории булевых функций, можно ограничиться ещё меньшим набором базовых операций. Есть также языки программирования, где существует встроенная возможность выполнить любую бинарную логическую операцию побитово. Например, в PL/I есть встроенная функция BOOL, третий аргумент которой предназначен для указания произвольной логической операции, которую необходимо побитово применить к первым двум аргументам[3]. Битовые сдвигиК битовым операциям также относят битовые сдвиги. При сдвиге значения битов копируются в соседние по направлению сдвига. Различают несколько видов сдвигов — логический, арифметический и циклический, в зависимости от обработки крайних битов. Также различают сдвиг влево (в направлении от младшего бита к старшему) и вправо (в направлении от старшего бита к младшему).  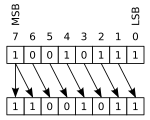 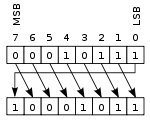  Логический сдвигПри логическом сдвиге значение последнего бита по направлению сдвига теряется (копируясь в бит переноса), а первый приобретает нулевое значение. Арифметический сдвигАрифметический сдвиг аналогичен логическому, но число считается знаковым, представленным в дополнительном коде. Так, при правом сдвиге старший бит сохраняет своё значение. Левый арифметический сдвиг идентичен логическому. Арифметические сдвиги влево и вправо используются для быстрого умножения и деления на 2. Циклический сдвигПри циклическом сдвиге, значение последнего бита по направлению сдвига копируется в первый бит (и копируется в бит переноса). Также различают циклический сдвиг через бит переноса — при нём первый бит по направлению сдвига получает значение из бита переноса, а значение последнего бита сдвигается в бит переноса. В языках программированияВстроенные операторы и функции, реализующие побитовые логические операции в некоторых языках программирования:
2-адическая интерпретацияЦелое число, записанное (в дополнительном коде) в бесконечный (в сторону положительных степеней двойки) двоичный регистр является естественным объектом для теории p-адических чисел при . Множество целых 2-адических чисел (то есть произвольных бесконечных битовых последовательностей) может быть рассмотрено как булева алгебра точно так же как и множество значений битового регистра конечной длины. Все вышеперечисленные битовые операции оказываются непрерывными отображениями. Хотя практическое программирование не располагает регистрами бесконечной длины, это не мешает использовать данный теоретический факт в криптографии для создания быстродействующих алгоритмов шифрования. Практические примененияФизическая реализация битовых операцийРеализация битовых операций может в принципе быть любой: механической (в том числе гидравлической и пневматической), химической, тепловой,[9] электрической, магнитной и электромагнитной (диапазоны — ИК, видимый оптический, УФ и далее по убыванию длин волн), а также в виде комбинаций, например, электромеханической. В первой половине XX века до изобретения транзисторов применяли электромеханические реле и электронные лампы. В пожароопасных и взрывоопасных условиях до сих пор применяют пневматические логические устройства (пневмоника). Наиболее распространены электронные реализации битовых операций при помощи транзисторов, например резисторно-транзисторная логика (РТЛ), диодно-транзисторная логика (ДТЛ), эмиттерно-связанная логика (ЭСЛ), транзисторно-транзисторная логика (ТТЛ), N-МОП-логика, КМОП-логика и др. В квантовых вычислениях из перечисленных булевых операций реализуются только НЕ и искл. ИЛИ (с некоторыми оговорками). Квантовых аналогов И, ИЛИ и т. д. не существует. Схемы аппаратной логикиРезультат операции ИЛИ-НЕ или ИЛИ от всех битов двоичного регистра проверяет, равно ли значение регистра нулю; то же самое, взятое от выхода искл. ИЛИ двух регистров, проверяет равенство их значений между собой. Битовые операции применяются в знакогенераторах и графических адаптерах. Использование в программированииБлагодаря реализации в арифметико-логическом устройстве (АЛУ) процессора многие регистровые битовые операции аппаратно доступны в языках низкого уровня. В большинстве процессоров реализованы в качестве инструкции регистровый НЕ; регистровые двухаргументные И, ИЛИ, исключающее ИЛИ; проверка равенства нулю (см. выше); три типа битовых сдвигов, а также циклические битовые сдвиги. Регистровая операция И используется для:
Регистровая операция ИЛИ используется для:
Регистровая операция исключающее ИЛИ используется для инвертирования битов регистра по маске. Сдвиги влево и вправо используются для умножения на 2 и целочисленного деления на 2 соответственно и выделения отдельных битов. Так, например, в сетевых интернет-технологиях операция И между значением IP-адреса и значением маски подсети используется для определения принадлежности данного адреса к подсети. Примечания
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

