|
Triângulo de Reuleaux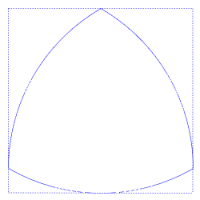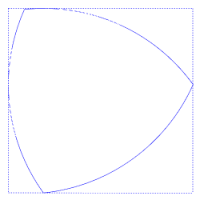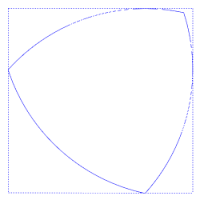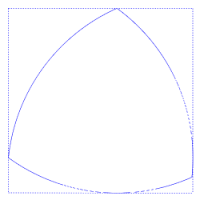 O triângulo de Reuleaux (ou triângulo esférico) é o exemplo mais simples dos chamados polígonos de Reuleaux. O nome é uma homenagem ao cientista e engenheiro que os desenvolveu, Franz Reuleaux. Estes polígonos tem a distinção de serem curvas de largura constante, ou seja, a distância entre os duas retas tangentes paralelas opostas é a mesma, independentemente da direção destas retas. Isto é mostrado na figura anexa, em que há sempre quatro pontos de contato com o quadrado, uma de cada lado.[1] Construção Um triângulo de Reuleaux pode ser tanto construído diretamente a partir de três círculos, ou pelo arredondamento dos lados de um triângulo equilátero.[2] A construção com três círculos pode ser realizada com compasso sozinho, sem a necessidade de uma régua. Pelo teorema de Mohr-Mascheroni, o mesmo vale para qualquer construção com régua e compasso,[3] mas a construção do triângulo de Reuleaux é particularmente simples: Primeiro, usa-se o compasso para desenhar o círculo, ou um arco circular suficientemente grande. Em seguida, mantendo-se fixa a abertura do compasso, coloca-se a ponta do compasso sobre o círculo ou arco, e desenha-se um segundo círculo ou arco passando pelo centro do primeiro. Finalmente, com a ponta do compasso em um dos dois pontos de interseção dos dois círculos, desenha-se um terceiro círculo ou arco de mesmo raio, através dos centros dos dois primeiros círculos. A região central do arranjo correspondente de três círculos é um triângulo de Reuleaux.[2] Alternativamente, constrói-se um triângulo equilátero T. Então desenha-se os arcos dos círculos, cada um centrado em um vértice de T e conectando os outros dois vértices.[4] Outros ficheiros
Referências
|
