|
Smoothsort
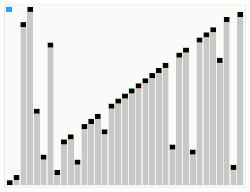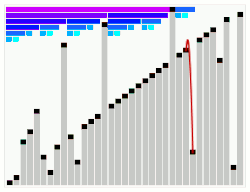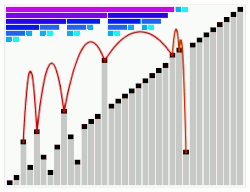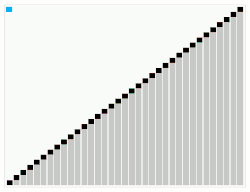
Smoothsort[1][2] (método) é um algoritmo de ordenação de ordenação por comparação. É uma variação do heapsort e foi desenvolvido por Edsger Dijkstra em 1981. Como o heapsort, o limite superior do smoothsort é de O(n log n). A vantagem de smoothsort é que ele se aproxima de tempo O(n) se a entrada já tem algum grau de ordenação, enquanto a média do heapsort é de O(n log n), independentemente do estado inicial em termos de ordenação. PanoramaO array a ser ordenado é dividido em uma string de heaps, cada heap com um tamanho igual a um dos números de Leonardo L(n). O processo de divisão é simples — os nós mais à esquerda do array são feitos no maior heap possível, e o restante é dividido igualmente. Pode ser provado que
Cada heap, tendo um tamanho de L(x), é estruturado a partir da esquerda para a direita como um sub-heap de tamanho L(x-1), uma sub-heap de tamanho L(x-2), e um nó raiz, com excepção dos heaps com um tamanho de L(1) e L(0) (que por definição são 1). Cada heap mantém a propriedade de heap onde um nó raiz é sempre >= os nodos raízes de seus heap-filhos (e, portanto, >= todos os nós em seus heaps filhos), e a string de heaps como um todo mantém a propriedade da string que o nó raiz de cada heap é >= nó raiz do heap para a esquerda. A consequência disto é que o nó mais à direita na string será sempre maior ou igual a todos os outros nós, e mais importante — um array que já está ordenado não precisa de nenhuma reorganização a ser feita em uma série válida de heaps. Esta é a origem das qualidades de adaptação do algoritmo. O algoritmo é simples. Começamos por dividir nosso arry não-ordenado em um único heap de um elemento, seguido por uma porção não ordenada. O array de um elemento é trivialmente uma seqüência válida de heaps. Esta seqüência é, então, acrescida pela adição de um elemento de cada vez para a direita, realizando trocas para manter a propriedade da seqüência e a propriedade do heap, até preencher todo o array original. Deste ponto em diante, o elemento mais à direita da sequência de heaps será o maior elemento em qualquer um dos heaps, e será, portanto, em sua posição final correta. Em seguida, reduzimos a série de heaps de volta a um único heap de um elemento, removendo o nó mais à direita (que permanece no local) e realizamos re-arranjos para restabelecer a condição de heap. Quando reduzimos para um único heap de um elemento, o array é ordenado. Heapsort e árvores de LeonardoO Heapsort, é baseado em uma estrutura de dados denominada heap. Um heap é uma árvore estritamente binária que satisfaz a seguinte propriedade: dado qualquer elemento da árvore, este será sempre maior ou igual que seus filhos diretos. Considerando a transitividade, cada elemento é maior ou igual que todos os seus descendentes na árvore. A árvore é, na verdade, implícita, simulada em um vetor, fazendo com que cada elemento no vetor com índice i seja pai dos elementos com índice (i*2)+1 e (i*2)+2 (considerando o endereço inicial do array igual a zero). A ordenação de um vetor com n elementos, pelo Heapsort é feita em dois passos:
O Heapsort é um excelente método de ordenação, tendo complexidade de pior caso igual a O(n log n), que é o melhor que se pode obter. Ele tem também complexidade de caso médio, O(n log n) e, por isso, é um método de ordenação de uso geral. Além disso, o método não exige memória adicional para a ordenação. Os números de Leonardo formam uma sequência parecida com a dos números de Fibonacci. Indicaremos por Ln o n-ésimo número de Leonardo e Fn o n-ésimo número de Fibonacci. Assim sendo, as fórmulas conhecidas para os números de Fibonacci podem ser usadas no estudo dos números de Leonardo sem muito esforço. Assim como os números de Fibonacci, os números de Leonardo também são definidos por uma recorrência: L0 = 1, L1 = 1, Ln = Ln - 1 + Ln -2 + 1 Os 20 primeiros números de Leonardo são os seguintes: 1, 1, 3, 5, 9, 15, 25, 41, 67, 109, 177, 287, 465, 753, 1219, 1973, 3193, 5167, 8361 e 13529. Pode-se mostrar que a relação entre Ln e Fn é dada por: Ln = 2Fn - 1. Observando atentamente a recorrência que gera os números de Leonardo é fácil perceber que esses números podem ser usados para construir uma árvore binária de forma recursiva: Ln = Ln - 1 + Ln -2 + 1. Cada número é formado somando-se dois números anteriores mais um, portanto é possível criar uma árvore binária onde a raiz da árvore tem Ln-1 filhos à esquerda e Ln-2 filhos à direita. Com isso a árvore inteira tem Ln elementos, e como Ln = Ln-1 + Ln-2 + 1, tem-se que Ln-1 corresponde à subárvore esquerda, Ln-2 à sub-árvore direita e 1 corresponde à raiz da árvore, pois a raiz só tem um elemento. A seguir, um exemplo numérico ilustra melhor como fazer uma árvore dessa forma. Na Figura temos uma árvore binária com 9 elementos. Na raiz dessa árvore aparece o número nove, o maior valor. Os antecessores de 9 na seqüência dos números de Leonardo são 5 e 3 e assim sucessivamente. Esse tipo de representação em árvore pode ser feito de forma implícita, usando-se um array de elementos. A partir de agora, este tipo de árvore será chamada de árvore de Leonardo. Ocorre que nem todos os arrays possuem dimensão igual a um dos números de Leonardo. Portanto, nem todos os arrays podem ser acessados como se fossem uma árvore de Leonardo implícita, mas podem ser acessados como se fossem um conjunto de árvores de Leonardo implícitas. Um conjunto de árvores de Leonardo é chamado de floresta de Leonardo. A floresta de Leonardo que tenha o menor número de árvores pode ser criada de forma gulosa. O procedimento guloso consiste em percorrer o vetor da esquerda para a direita e, para cada nova posição do vetor, considerar essa posição como a raiz, ou de uma árvore com apenas um nó, ou como uma nova raiz para as duas últimas árvores criadas, desde que os números de nós das duas representem números consecutivos (em ordem decrescente) de Leonardo. Desta forma, claramente a maior árvore de Leonardo para um vetor com n elementos corresponde à primeira árvore da floresta e o número de nós da mesma é o maior número de Leonardo contido em n. Sucessivamente isso vale para o restante do vetor. No artigo original sobre o Smoothsort, Dijkstra deixou a prova desse problema para o leitor. O algoritmo SmoothsortNesta seção descreveremos resumidamente o funcionamento do Smoothsort. O algoritmo é parecido com o Heapsort, no sentido de que cria, em um primeiro passo, várias árvores, tal que as raízes das árvores devem ser maiores que todos os demais elementos, e a raiz de cada sub-árvore deve manter essa mesma propriedade. Para construir a floresta a partir do vetor, o Smoothsort considera um elemento do vetor de cada vez. Se as duas últimas árvores da floresta tiverem tamanhos correspondentes a dois números consecutivos da seqüência de Leonardo, então essas duas árvores junto com o elemento adicionado se juntam e formam uma nova árvore da floresta, conforme a recorrência: Ln = Ln-1 + Ln-2 + 1. Na floresta tem-se que Ln-1 corresponde à penúltima árvore e Ln-2 corresponde à última árvore. A princípio, observando a construção dessa floresta com cinco elementos, pode-se pensar que as duas últimas árvores irão sempre se tornar filhas de um novo elemento que seja adicionado. No entanto, isto não é verdade. Seguindo-se esse processo simples é possível construir uma floresta de Leonardo implicitamente sobre arrays de qualquer tamanho. Para que os dados fiquem ordenados, o Smoothsort faz a floresta de árvores de Leonardo funcionar como se fosse um grande heap, de modo que a raiz de cada árvore de Leonardo sempre contém o maior elemento da árvore, e as raízes das sub-árvores também tenham essa mesma propriedade. No entanto como o Smoothsort não cria apenas uma árvore e sim várias árvores, é preciso que, além disso, haja alguma ordenação entre essas árvores. A ordenação que é feita consiste em fazer com que a raiz de uma árvore de Leonardo seja sempre maior ou igual às raízes de todas as outras árvores de Leonardo que estiverem à esquerda. Na segundo passo faz-se a ordenação da floresta (função OrdenaFloresta), retirando-se sempre a raiz mais à direita do vetor e acertando as árvores restantes, de forma que a propriedade de heap continue valendo. Quando se retira a raiz mais à direita, ela é com certeza a maior chave do início do vetor até o ponto considerado. A sua retirada, quando a raiz é o único nó da árvore, diminui o número de árvores de Leonardo. Entretanto, se não for o nó único, as subárvores dessa árvore são acrescentadas ao conjunto de árvores de Leonardo. Neste caso, pode ser necessário acertar a ordenação das raízes, pois não se tem garantia que a introdução de duas novas árvores ao conjunto tenha essa propriedade necessária. OperaçõesIgnorando (no momento) as otimizações de Dijkstra, duas operações são necessárias — aumentar a string, adicionando um elemento para a direita, e diminuir a string removendo o elemento mais à direita (a raiz do heap passado), preservando o heap e as condições da string. Aumentar a string, adicionando um elemento para a direita
Após isto, o heap e as propriedades da string devem ser restaurados. Para fazer isso,
A operação do filtro é bastante simplificada pelo uso de números de Leonardo, pois um heap será sempre um único nó, ou terá dois heaps-filho. Não é preciso se tratar a condição de um dos heaps-filho não estar presente. Optimização
Encolher a seqüência pela remoção do elemento mais à direitaSe o heap mais à direita tem um tamanho de 1 (ou seja, L(1) ou L(0)), então nada precisa ser feito. Basta remover o heap mais à direita. Se o heap mais à direita não tem um tamanho de 1, em seguida, remover a raiz, mostrando os dois sub-heaps, como membros da string. Restaurar a propriedade de string primeiro na esquerda e, em seguida, na direita. Otimização
Implementação em JavaEste código usa lo e hi como as os limites do array inclusive. Note-se que esta não é a convenção usual. // mantendo essas constantes, podemos evitar o negócio cansativo
// de acompanhar o b e o c de Dijkstra. Em vez de manter
// b e c, Eu irei manter um índice dentro do array
static final int LP[] = { 1, 1, 3, 5, 9, 15, 25, 41, 67, 109,
177, 287, 465, 753, 1219, 1973, 3193, 5167, 8361, 13529, 21891,
35421, 57313, 92735, 150049, 242785, 392835, 635621, 1028457,
1664079, 2692537, 4356617, 7049155, 11405773, 18454929, 29860703,
48315633, 78176337, 126491971, 204668309, 331160281, 535828591,
866988873 // the next number is > 31 bits.
};
public static <C extends Comparable<? super C>> void sort(C[] m,
int lo, int hi) {
int head = lo; // o deslocamento do primeiro elemento do prefixo em m
// Essas variáveis precisam de um pouco de explicação. Se a nossa string de heaps
// é de tamanho 38, então os heaps serão de tamanho 25+9+3+1, que são os
// números de Leonardo 6, 4, 2, 1.
// Passando este int um número binário, temos b01010110 = x56. Nós representamos
// este número como um par de números, através de deslocamentos à direita de todos os zeros
// armazenando a mantissa e o expoente como "p" e "pshift".
// Isso é útil, porque o expoente é o índice em L [] dando o
// tamanho fo heap mais a direita, e porque nós podemos imediatamente verificar se
// os dois heaps mais a direita são números consecutivos de leonardo, verificando
// (p&3)==3
int p = 1; // o bitmap da concatenação padrão atual >> pshift
int pshift = 1;
while (head < hi) {
if ((p & 3) == 3) {
// Soma 1 intercalando os dois primeiros blocos em um bloco maior.
// O próximo número de Leonardo é maior em um.
sift(m, pshift, head);
p >>>= 2;
pshift += 2;
} else {
// somando um novo bloco de tamanho 1
if (LP[pshift - 1] >= hi - head) {
// this block is its final size.
trinkle(m, p, pshift, head, false);
} else {
// este bloco esrá intercalado.
sift(m, pshift, head);
}
if (pshift == 1) {
// LP[1] está sendo usado, logo nós adicionamos o uso de LP[0]
p <<= 1;
pshift--;
} else {
// shift out to position 1, add LP[1]
p <<= (pshift - 1);
pshift = 1;
}
}
p |= 1;
head++;
}
trinkle(m, p, pshift, head, false);
while (pshift != 1 || p != 1) {
if (pshift <= 1) {
// bloco de comprimento 1. Nenhum fiddling necessário
int trail = Integer.numberOfTrailingZeros(p & ~1);
p >>>= trail;
pshift += trail;
} else {
p <<= 2;
p ^= 7;
pshift -= 2;
// ok. Este bloco é quebrado em três pedaços. O bit mais à direita
// é um bloco de tamanho. A parte da esquerda é dividida em dois,
// um bloco de tamanho LP[pshift+1] e um de LP[pshift].
// Ambos os dois são adequadamente heaps formados, mas os nodos raiz
// não estão necessariamente ordenados.
// Por isso, chamamos trinkle para ambos
trinkle(m, p >>> 1, pshift + 1, head - LP[pshift] - 1, true);
trinkle(m, p, pshift, head - 1, true);
}
head--;
}
}
private static <C extends Comparable<? super C>> void sift(C[] m, int pshift,
int head) {
C val = m[head];
while (pshift > 1) {
int rt = head - 1;
int lf = head - 1 - LP[pshift - 2];
if (val.compareTo(m[lf]) >= 0 && val.compareTo(m[rt]) >= 0)
break;
if (m[lf].compareTo(m[rt]) >= 0) {
m[head] = m[lf];
head = lf;
pshift -= 1;
} else {
m[head] = m[rt];
head = rt;
pshift -= 2;
}
}
m[head] = val;
}
private static <C extends Comparable<? super C>> void trinkle(C[] m, int p,
int pshift, int head, boolean isTrusty) {
C val = m[head];
while (p != 1) {
int stepson = head - LP[pshift];
if (m[stepson].compareTo(val) <= 0)
break; // o nodo corrente é maior que a cabeça. peneirar.
// não há necessidade de checar isso, se sabemos que o nodo atual é confiável,
// porque nós já checamos a cabeça (que é val, na primeira iteração)
if (!isTrusty && pshift > 1) {
int rt = head - 1;
int lf = head - 1 - LP[pshift - 2];
if (m[rt].compareTo(m[stepson]) >= 0
|| m[lf].compareTo(m[stepson]) >= 0)
break;
}
m[head] = m[stepson];
head = stepson;
int trail = Integer.numberOfTrailingZeros(p & ~1);
p >>>= trail;
pshift += trail;
isTrusty = false;
}
if (!isTrusty) {
m[head] = val;
sift(m, pshift, head);
}
}
Implementação em C++
/*****Please include following header files*****/
// string.h
/***********************************************/
typedef char* String;
#define IsAscending(A,B) (strcmp(A,B) <= 0)
#define UP(IA,IB) temp = IA; IA += IB + 1; IB = temp;
#define DOWN(IA,IB) temp = IB; IB = IA - IB - 1; IA = temp;
static int q, r, p, b, c, r1, b1, c1;
static String* A;
static void Sift()
{
int r0, r2, temp;
String t;
r0 = r1;
t = A[r0];
while (b1 >= 3)
{
r2 = r1 - b1 + c1;
if (!IsAscending(A[r1 - 1], A[r2]))
{
r2 = r1 - 1;
DOWN(b1, c1);
}
if (IsAscending(A[r2], t))
{
b1 = 1;
}
else
{
A[r1] = A[r2];
r1 = r2;
DOWN(b1, c1);
}
}
if (r1 - r0)
A[r1] = t;
}
static void Trinkle()
{
int p1, r2, r3, r0, temp;
String t;
p1 = p;
b1 = b;
c1 = c;
r0 = r1;
t = A[r0];
while (p1 > 0)
{
while ((p1 & 1) == 0)
{
p1 >>= 1;
UP(b1, c1)
}
r3 = r1 - b1;
if ((p1 == 1) || IsAscending(A[r3], t))
{
p1 = 0;
}
else
{
--p1;
if (b1 == 1)
{
A[r1] = A[r3];
r1 = r3;
}
else
{
if (b1 >= 3)
{
r2 = r1 - b1 + c1;
if (!IsAscending(A[r1 - 1], A[r2]))
{
r2 = r1 - 1;
DOWN(b1, c1);
p1 <<= 1;
}
if (IsAscending(A[r2], A[r3]))
{
A[r1] = A[r3]; r1 = r3;
}
else
{
A[r1] = A[r2];
r1 = r2;
DOWN(b1, c1);
p1 = 0;
}
}
}
}
}
if (r0 - r1)
A[r1] = t;
Sift();
}
static void SemiTrinkle() {
String T;
r1 = r - c;
if (!IsAscending(A[r1], A[r]))
{
T = A[r];
A[r] = A[r1];
A[r1] = T;
Trinkle();
}
}
static void SmoothSort(String Aarg[], const int N) {
int temp;
A = Aarg;
q = 1;
r = 0;
p = 1;
b = 1;
c = 1;
while (q < N) {
r1 = r;
if ((p & 7) == 3)
{
b1 = b;
c1 = c;
Sift();
p = (p + 1) >> 2;
UP(b, c);
UP(b, c);
}
else if ((p & 3) == 1) {
if (q + c < N)
{
b1 = b;
c1 = c;
Sift();
}
else
{
Trinkle();
}
DOWN(b, c);
p <<= 1;
while (b > 1)
{
DOWN(b, c);
p <<= 1;
}
p++;
}
q++;
r++;
}
r1 = r;
Trinkle();
while (q > 1)
{
--q;
if (b == 1)
{
r--;
p--;
while ((p & 1) == 0)
{
p >>= 1;
UP(b, c);
}
}
else
{
if (b >= 3) {
p--;
r = r - b + c;
if (p > 0)
SemiTrinkle();
DOWN(b, c);
p = (p << 1) + 1;
r = r + c;
SemiTrinkle();
DOWN(b, c);
p = (p << 1) + 1;
}
}
}
}
Implementação em PHP
function IsAscending($A, $B)
{
return (strcmp($A, $B) <= 0);
}
function UP(&$IA, &$IB, &$temp)
{
$temp = $IA;
$IA += $IB + 1;
$IB = $temp;
}
function DOWN(&$IA, &$IB, &$temp)
{
$temp = $IB;
$IB = $IA - $IB - 1;
$IA = $temp;
}
$q; $r; $p; $b; $c; $r1; $b1; $c1;
$A = array();
function Sift()
{
global $r1, $b1, $c1, $A;
$r0; $r2; $temp = 0;
$t = "";
$r0 = $r1;
$t = $A[$r0];
while ($b1 >= 3)
{
$r2 = $r1 - $b1 + $c1;
if (!IsAscending($A[$r1 - 1], $A[$r2]))
{
$r2 = $r1 - 1;
DOWN($b1, $c1, $temp);
}
if (IsAscending($A[$r2], $t))
{
$b1 = 1;
}
else
{
$A[$r1] = $A[$r2];
$r1 = $r2;
DOWN($b1, $c1, $temp);
}
}
if ($r1 - $r0)
$A[$r1] = $t;
}
function Trinkle()
{
global $p, $b, $c, $r1, $b1, $c1, $A;
$p1; $r2; $r3; $r0; $temp = 0;
$t = "";
$p1 = $p;
$b1 = $b;
$c1 = $c;
$r0 = $r1;
$t = $A[$r0];
while ($p1 > 0)
{
while (($p1 & 1) == 0)
{
$p1 >>= 1;
UP($b1, $c1, $temp);
}
$r3 = $r1 - $b1;
if (($p1 == 1) || IsAscending($A[$r3], $t))
{
$p1 = 0;
}
else
{
--$p1;
if ($b1 == 1)
{
$A[$r1] = $A[$r3];
$r1 = $r3;
}
else
{
if ($b1 >= 3)
{
$r2 = $r1 - $b1 + $c1;
if (!IsAscending($A[$r1 - 1], $A[$r2]))
{
$r2 = $r1 - 1;
DOWN($b1, $c1, $temp);
$p1 <<= 1;
}
if (IsAscending($A[$r2], $A[$r3]))
{
$A[$r1] = $A[$r3]; $r1 = $r3;
}
else
{
$A[$r1] = $A[$r2];
$r1 = $r2;
DOWN($b1, $c1, $temp);
$p1 = 0;
}
}
}
}
}
if ($r0 - $r1)
$A[$r1] = $t;
Sift();
}
function SemiTrinkle()
{
global $r, $c, $r1, $A;
$T = "";
$r1 = $r - $c;
if (!IsAscending($A[$r1], $A[$r]))
{
$T = $A[$r];
$A[$r] = $A[$r1];
$A[$r1] = $T;
Trinkle();
}
}
function SmoothSort($Aarg, $N)
{
global $q, $r, $p, $b, $c, $r1, $b1, $c1, $A;
$temp = 0;
$A = $Aarg;
$q = 1;
$r = 0;
$p = 1;
$b = 1;
$c = 1;
while ($q < $N)
{
$r1 = $r;
if (($p & 7) == 3)
{
$b1 = $b;
$c1 = $c;
Sift();
$p = ($p + 1) >> 2;
UP($b, $c, $temp);
UP($b, $c, $temp);
}
else if (($p & 3) == 1)
{
if ($q + $c < $N)
{
$b1 = $b;
$c1 = $c;
Sift();
}
else
{
Trinkle();
}
DOWN($b, $c, $temp);
$p <<= 1;
while ($b > 1)
{
DOWN($b, $c, $temp);
$p <<= 1;
}
++$p;
}
++$q;
++$r;
}
$r1 = $r;
Trinkle();
while ($q > 1)
{
--$q;
if ($b == 1)
{
--$r;
--$p;
while (($p & 1) == 0)
{
$p >>= 1;
UP($b, $c, $temp);
}
}
else
{
if ($b >= 3)
{
--$p;
$r = $r - $b + $c;
if ($p > 0)
SemiTrinkle();
DOWN($b, $c, $temp);
$p = ($p << 1) + 1;
$r = $r + $c;
SemiTrinkle();
DOWN($b, $c, $temp);
$p = ($p << 1) + 1;
}
}
}
return $A;
}
Referências
Bibliografia
Ligações externas |
||||||||||||||||||||