|
Rombicosidodecaedro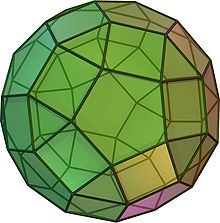 Em geometria, o rombicosidodecaedro, ou pequenas rombicosidodecaedro, é um sólido de Arquimedes, um dos treze sólidos convexos isogonais não prismáticos construídos a partir de faces de dois ou mais tipos de polígonos regulares. Tem 62 faces, das quais 20 são triângulos regulares, 30 são quadrados, e 12 são pentágonos regulares, 60 vértices e 120 arestas. O nome rombicosidodecaedro refere-se ao fato de que as 30 faces quadradas ficam no mesmo plano, como as 30 faces do triacontaedro rômbico que é dual para o icosidodecaedro. Ele também pode ser chamado de um expandido dodecaedro ou icosaedro, a partir de operações de truncamento no poliedro uniforme. Relações geométricasSe você expandir um icosaedro movendo sua face para longe da origem, na quantidade certa, sem alterar a orientação ou tamanho das faces, e fazer o mesmo com o seu dodecaedro dual e o trecho dos buracos do quadrados no resultado, você obtém um rombicosidodecaedro. Portanto, ele tem o mesmo número de triângulos como um icosaedro e o mesmo número de pentágonos como um dodecaedro, com um quadrado para cada aresta de qualquer outro. O rombicosidodecaedro ações vértice de um acordo com o pequeno estrelado dodecaedro truncado, e com o uniforme de compostos de seis ou doze pentagrammic prismas. O Zometool kits para fazer cúpulas geodésicas e outros poliedros uso de fenda bolas como conectores. As bolas são "expandido" rhombicosidodecahedra, com as praças substituído por retângulos. A expansão é escolhido de modo que a resultante retângulos são retângulos áureos. Coordenadas cartesianasAs coordenadas cartesianas para os vértices de um rombicosidodecaedro com o comprimento da aresta 2 centrada na origem, são todas permutações de:[1]
onde φ = 1 + √52 é a razão de ouro. Projeções ortogonaisO rombicosidodecaedro tem cinco especial projeções ortogonais, centralizado, em um vértice, em dois tipos de bordas, e três tipos de faces: triângulos, quadrados e pentágonos. Os dois últimos correspondem a A2 e H2 nos planos Coxeter.
Ladrilhos esféricosO rombicosidodecaedro também pode ser representado como ladrilhos esféricos, e projetados para o plano através de uma projeção estereográfica. Esta projeção é conformal, preservanvando os ângulos, mas não áreas ou comprimentos. Linhas retas sobre a esfera são projetados como arcos circulares no plano.
Poliedros relacionados Mutações simétricasEste poliedro é topologicamente relacionado como parte de uma sequência de poliedros cantilados com vértice na figura 3.4.n.4), que continua como estrutura do plano hiperbólico. Esta figura de vértice-transitivo (*n32) tem simetria reflexiva. Sólidos de JohnsonExistem 13 Sólidos de Johnson relacionados, 5 por diminuição, e 8 incluindo rotações:
Arranjo do vérticeO rombicosidodecaedro compartilha seu arranjo de vértice com três poliedros uniformes não convexos: o pequeno dodecaedro estrelado truncado, o pequeno dodecicododecaedro (tendo a forma triangular e faces pentagonais em comum), e o pequeno rombidodecaedro (com faces quadradas em comum). Ele também compartilha seu arranjo de vértice com o poliedro uniforme e compostos de seis ou doze prismas pentagramas.
Gráfico do rombicosidodecaedroEm matemática no campo da teoria dos grafos, um gráfico do rombicosidodecaedro é o gráfico de vértices e arestas do rombicosidodecaedro, um dos sólidos de Arquimedes. Ele tem 60 vértices e 120 bordas, e é um gráfico quártico dos gráficos de Arquimedes.[2]
Veja tambémNotas
Referências
Ligações externas
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||




































